Problemas
No todo van a ser cuentas...
En las unidades anteriores hemos resuelto problemas con poco más que las operaciones básicas. Ahora podemos usar las ecuaciones de primer y segundo grado para resolverlos. Los consejos a la hora de enfrentarte a un enunciado siguen siendo los mismos, pero ahora deberás ser capaz también de transformar la información que te da el problema en una ecuación que relacione los datos conocidos con los desconocidos (incógnitas).
OBSERVACIÓN Cuando te enfrentes a un problema de matemáticas (o de otra materia).
- Lee el enunciado con tranquilidad. Es importante que entiendas lo que pone. La información no está expuesta de manera directa como en un ejercicio de cálculo, hay que encontrarla entre el texto.
- Localiza la pregunta o preguntas que tengas que resolver. Es importante saber qué es lo que te pide el problema, si no, difícilmente podremos preparar una estrategia.
- Ordena toda la información útil que te da el problema para resolver la pregunta que te plantea. No todos los datos tienen por qué ser necesarios para llegar a una respuesta.
- A la hora de seguir una estrategia u otra, sería interesante estudiar si los datos que tienes te permiten aplicarla, si va a ser eficiente para el problema que tienes entre manos... pero no es obligatorio acertar a la primera. Al principio puede parecer difícil escoger "por dónde tirar", pero la práctica te dará soltura. Muchos problemas se parecen entre ellos. De hecho es algo "muy matemático" intentar utilizar estrategias que han funcionado previamente para solucionar problemas nuevos.
- Si llegas a una respuesta, comprueba que tiene sentido. No sería la primera vez que alguien dice que "Pedro tiene
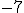años"...
Fíjate en el siguiente ejemplo:
Enunciado: Carla y Javier tienen tres hijos. El mayor es cuatro años mayor que el mediano y éste es tres años mayor que el pequeño. Si entre los tres suman 40 años, ¿qué edad tiene cada uno de los hermanos?
En la siguiente tabla tienes una explicación de los pasos a dar para resolver el problema.
|
PRIMER PASO: Identificamos lo que nos pide el problema y asignamos variables. Nos pide la edad de cada uno de los tres hermanos. Son tres incógnitas, pero sólo podemos usar una variable. Afortunadamente, conocemos relaciones entre las edades de los hermanos que nos permiten arreglarnos usando sólo una letra. |
Edad del mayor: Edad del mediano: Edad del menor: |
|
SEGUNDO PASO: Expresamos matemáticamente la condición que da el enunciado mediante una ecuación. La condición es que las edades de los tres hermanos sumen 40 años. |
 |
|
TERCER PASO: Resolvemos la ecuación. |
 |
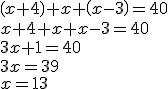| CUARTO PASO: Comprobamos el resultado y redactamos una respuesta. |
Edad del mayor: Edad del mediano: Edad del menor:
RESPUESTA: El mayor tiene 17 años, el mediano 13 y el pequeño 10. |
Los problemas que aquí se proponen están pensados para que trabajes con ellos en tu libreta y luego compruebes la respuesta que has obtenido.
Problema 1
El perímetro de un jardín rectangular es 58 m. Si el lado mayor mide 11 m más que el lado menor, ¿canto miden los lados del jardín?
RESPUESTA: Los dos lados mayores miden m cada uno y los dos menores m cada uno.
Problema 2
Halla un número tal que su mitad más su cuarta parte más uno sea igual al propio número.
RESPUESTA: El número buscado es .
Problema 3
Hace 13 años, la edad de un Juan era el triple que la edad de su hija Ana. Si Juan tenía 34 años cuando nació Ana, ¿qué edad tienen ambos?
RESPUESTA: Juan tiene años y Ana .
Problema 4
Dos depósitos de agua tienen la misma capacidad. Al comienzo del día estaban completamente llenos, pero de uno de ellos se han retirado 1300 litros y del otro 5350 litros, de modo que en el primero queda el triple de agua que en el segundo. ¿Cuál es la capacidad de los depósitos?
RESPUESTA: Cada depósito tiene una capacidad de litros.
Problema 5
Laura tiene 32 años menos que su padre y éste tiene el triple de años que su hija. Obtén la edad de cada uno.
RESPUESTA: Laura tiene años y su padre tiene .
Problema 6
Un examen consta de 50 preguntas, cada una con cinco posibles respuestas. Por cada respuesta correcta se dan 3 puntos y por cada respuesta incorrecta se quita un punto. Si una pregunta queda en blanco, no se puntúa. Un alumno que respondió a 42 preguntas tiene 58 puntos. ¿Cuántos aciertos tuvo?
RESPUESTA: El alumno tuvo aciertos.
Problema 7
En una granja, entre gallinas y conejos, hay un total de 600 animales. Si contásemos sus patas, obtendríamos 1480. ¿Cuántas gallinas y cuántos conejos hay?
RESPUESTA: En la granja hay conejos y gallinas.
Problema 8
Pedro tiene 7 años y su madre 31. ¿Cuántos años tienen que pasar para que la edad de la madre sea el triple que la de Pedro?
RESPUESTA: Tienen que pasar
años.
Problema 9
Cristina tiene 3375 € en billetes de 20 € y 5 €. Si tiene el doble de billetes de 20 € que de 5 €, ¿cuántos billetes tiene de cada tipo?
RESPUESTA: Cristina tiene billetes de 20 € y billetes de 5 €..
Problema 10
Encuentra cuatro números enteros consecutivos que sumen 50.
RESPUESTA: Los números buscados son , , y .
Problema 11
En un taller especializado en motos y coches hay 25 vehículos en total. Si entre todos los vehículos suman 72 ruedas, ¿cuántos coches y cuántas motos hay?
RESPUESTA: Hay motos y coches en el taller.
Problema 12
Un grupo de 24 alumnos está construyendo un cisne de papel por piezas. Hasta el momento, los alumnos trabajadores han conseguido una media de 8 piezas por cabeza, mientras que los alumnos vagos tienen una media de 2 piezas por persona. Si en total han construido 138 piezas, ¿cuántos alumnos vagos y cuántos trabajadores hay en clase?
RESPUESTA: En clase hay alumnos trabajadores y alumnos vagos.
Problema 13
Encuentra un número negativo tal que el doble de su cuadrado menos el triple del mismo número sea igual a 189.
RESPUESTA: El número buscado es .
Problema 14
Encuentra dos números naturales consecutivos tales que la suma de sus cuadrados sea 113.
RESPUESTA: Los números buscados son y .
Problema 15
Un patio rectangular tiene 8 m más de largo que de ancho. Calcula sus dimensións sabiendo que su tiene una superficie de 768 m2.
RESPUESTA: El patio mide m de ancho y m de largo..
Problema 16
Calcula las medidas de los lados de un triángulo rectángulo sabiendo que son tres números consecutivos.
RESPUESTA: Los lados miden , y unidades.
Problema 17
Calcula la medida del lado de una habitación cuadrada, sabiendo que otra rectangular que es la mitad de ancha, pero es 3 m más larga, tiene 9 m2 menos de superficie.
RESPUESTA: El lado de la habitación cuadrada mide metros.
Problema 18
Para cercar una finca rectangular de 750 m2 se han utilizado 110 m de valla. Calcula las dimensiones de la finca.
RESPUESTA: Los lados de la finca miden y metros.