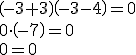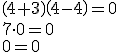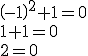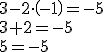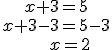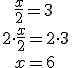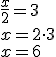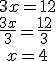Significado de las ecuaciones

¿Qué es una ecuación?

DEFINICIÓN Una ecuación es una igualdad entre dos expresiones algebraicas que establece una CONDICIÓN sobre la variable o variables que forman parte de dichas expresiones.

La idea es muy simple. Cuando queremos resolver un problema buscamos uno o varios elementos (en matemáticas se trata normalmente de un número) que cumplan las condiciones de dicho problema. Para describir los elementos que buscamos utilizamos variables, y sobre ellas tenemos que establecer las condiciones que marca el problema. Para establecer esas condiciones disponemos de las operaciones matemáticas, combinadas con las variables y números. Cuantas más operaciones matemáticas conozcamos, más complejas pueden ser las condiciones a establecer y, por tanto, más complicados pueden ser los problemas a resolver.

DEFINICIÓN Resolver una ecuación consiste en encontrar el valor o los valores de la variable que cumplen la condición marcada por la ecuación.

Fíjate en los siguientes ejemplos de ecuaciones:

ECUACIÓN	CONDICIÓN EN LENGUAJE CONVENCIONAL	SOLUCIÓN O SOLUCIONES	COMPROBACIÓN
	Un número menos dos unidades tiene que valer cinco.	La solución tiene que ser un número dos unidades mayor que , es decir, .
	El producto del resultado de sumar tres unidades a un número por el resultado de restar cuatro unidades a ese mismo número tiene que ser cero.	Para que el producto sea cero, alguno de los dos factores tiene que ser cero. Entonces, las soluciones son los opuestos de y , es decir, y .
	El cuadrado de un número más una unidad tiene que ser cero.	El cuadrado de cualquier número es siempre mayor o igual que cero y el número es positivo, así que es imposible conseguir que esa suma valga cero. La ecuación no tiene solución.	Ningún valor que pruebes cumplirá la condición. Por ejemplo:
	La suma de dos números tiene que ser cuatro.	Hay infinitas opciones válidas para cumplir la condición:	Hay infinitos valores que cumplen la condición. Por ejemplo:

No te preocupes si no entiendes alguno de los razonamientos anteriores. A lo largo de la unidad explicaremos con detalle cómo resolver las ecuaciones que corresponden a este curso, que serán aquellas cuyas expresiones sean polinomios de grado 1 o 2 y en una sola variable.

OBSERVACIÓN

Una igualdad entre expresiones algebraicas que no establece ninguna condición sobre las variables no se llama ecuación, sino identidad. Al no establecer condición alguna, una identidad es cierta para cualquier valor de las variables que aparezcan en las expresiones igualadas, de hecho, si aplicásemos a una identidad los métodos para obtener ecuaciones equivalentes, podríamos conseguir una igualdad sin variables. En la sección anterior de la unidad vimos tres ejemplos de identidades:

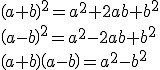
identidades_notables

No insistiremos en ello durante este curso, pero si te fijas en el último ejemplo, al utilizar más de una variable hay más "libertad" para escoger las soluciones (son infinitas). La idea es que añadir variables aumenta las opciones y añadir ecuaciones hace justo los contrario, las limita.

Ya sabemos lo que son las ecuaciones. Vamos a dejar claro cómo se llaman los elementos que aparecen en las mismas.

icono_definicion DEFINICIÓN En una ecuación (polinómica) podemos identificar los siguientes elementos:

Miembros de la ecuación: Son las expresiones que aparecen a ambos lados de la igualdad. Suele llamarse primer miembro al de la izquierda y segundo miembro al de la derecha, pero no es relevantes, ya que las posiciones son intercambiables (Es lo mismo escribir que ).

Términos: Son los monomios que forman cada uno de los miembros de la ecuación. Recuerda que los números pueden considerarse monomios de grado cero.

Incógnitas: Son las letras sobre las que la ecuación establece una condición.

Solución: Son los valores que deben tomar las incógnitas para cumplir la condición de la ecuación.

Grado: Es el mayor de los grados de los monomios que aparecen en la ecuación una vez ésta ha sido reducida (veremos después lo que significa reducir una ecuación).

Completa el siguiente ejercicio para comprobar si sabes identificar los elementos de una ecuación.

Ejercicio

Considera la siguiente ecuación y completa las frases. Haz en tu libreta las operaciones que sean necesarias.

a) e son las de la ecuación.

b) El grado de la ecuación es JXUwMDY5 .

c) es el de la ecuación y es el .

d) La ecuación tiene, tal y como está escrita, JXUwMDZl términos.

e) , JXUwMDJiJXUwMDll es solución de la ecuación.

f) , JXUwMDM2JXUwMDAx es solución de la ecuación.

¿Qué son ecuaciones equivalentes?

Fíjate bien en estas dos ecuaciones:

ECUACIÓN 1		ECUACIÓN 2

¿Cuál te parece más complicada? La primera tiene peor pinta... ¡pero en realidad son "iguales"! La única diferencia entre una y otra es que la primera no ha sido "tratada" aún para tener mejor aspecto, pero tienen la misma solución, es decir, establecen la misma condición sobre la variable. Por ejemplo, hay paréntesis que se pueden quitar (usando la propiedad distributiva), monomios semejantes que se pueden sumar o restar...

icono_definicion DEFINICIÓN Dos ecuaciones se dicen equivalentes si tienen las mismas soluciones.

En general, no será fácil resolver una ecuación directamente; tendremos que transformarla sucesivamente en otras equivalentes, cada vez más sencillas, hasta conseguir la solución.

¿Cómo se consiguen ecuaciones equivalentes? Lo primero sería completar todas las operaciones en ambos miembros de la ecuación. Después, puedes pensar en una ecuación como una balanza equilibrada. Cada uno sus dos miembros sería uno de los dos brazos de la balanza. La clave para que la balanza no pierda el equilibrio es quitar o poner siempre lo mismo en ambos brazos. Desde un punto de vista matemático, quitar o poner lo mismo en ambos brazos significa realizar la misma operación (suma, resta, multiplicación por un número distinto de cero o división entre un número distinto de cero) en ambos miembros de la ecuación.

En la siguiente tabla tienes una explicación detallada de todos los pasos necesarios para llegar desde la primera de las ecuaciones anteriores hasta la segunda:

La ecuación de partida es .

PASO	ESTADO DE LA ECUACIÓN
1º Quitamos paréntesis.
2º Sumamos y restamos monomios semejantes.
3º Restamos en ambos miembros.
4º Sumamos en ambos miembros.
5º Restamos en ambos miembros.

El objetivo es conseguir que los monomios con variable queden aislados en uno de los miembros de la ecuación (normalmente el primero) y que los números queden en el otro miembro. Si te fijas bien en los dos últimos pasos, parece que (en el cuarto paso) y (en el quinto paso) pasan de un miembro a otro de la ecuación cambiando su signo. Lo que haremos será interpretar de esa forma las operaciones en ambos miembros de una ecuación, para agilizar las cuentas. Esta idea recibe el nombre de transposición de términos.

icono_algoritmo ALGORITMO En la siguiente tabla están recogidas las operaciones que podemos hacer en ambos miembros de una ecuación para obtener otra equivalente.