Aproximaciones y notación científica
¿Es siempre posible ser preciso?
Imagina que estás planeando un viaje desde Melide hasta Barcelona. ¿Tendría sentido medir la distancia sobre un mapa a escala con una regla? ¿Sería esa una buena aproximación de la distancia real? ¿Harías el presupuesto para el viaje en función de esa medida? Quizá esa medida no sea extremadamente precisa, pero puede ser suficiente para calcular una buena aproximación del tiempo que durará el viaje.
Con frecuencia, la imprecisión en las medidas, la imposibilidad matemática (¿recuerdas los números irracionales?) o muchos otros motivos pueden forzarnos a sustituir un número exacto por otro próximo. Usar aproximaciones no es algo malo, es una necesidad, pero es muy importante controlar el error que se comete al usarlas.
Piensa en la siguiente situación: Un ayuntamiento encarga a un contratista la remodelación de una plaza circular de 
m de radio. Se acuerda un precio de 
€ el por m2 y el contratista presenta un presupuesto según la siguiente fórmula:
€
Como sabes, el área de un círculo está dada por la expresión 
, donde 
es el radio y 
un número irracional. El contratista está obligado a usar una aproximación para , pero ¿crees que es justo que utilice ésa?
En el siguiente applet puedes ver una representación en verde del área de la plaza para la aproximación que hace Geogebra de (muy buena aproximación) y, en rojo, la del área que realmente cubriría el contratista con su aproximación (muy mala). Casi no se aprecia la diferencia entre los dos círculos, pero esa diferencia es más notable entre los precios finales. Prueba a usar otras aproximaciones de más habituales (
o 
) para ver si las diferencias son menores.
¿Cómo aproximamos?
Cuando no tenemos más remedio que quedarnos con una aproximación de un número, ¿cómo escogemos esa aproximación? Lo más habitual es que no podamos escoger, de hecho, lo normal es no conocer el valor real, sino la aproximación. Sin embargo, si tenemos la posibilidad de escoger, tenemos dos opciones.
ALGORITMO Para aproximar un número cualquiera del que conocemos varias de sus cifras:
- Escogemos la posición a la que queremos aproximar, llamada orden de aproximación (no tiene que ser necesariamente una posición decimal).
- Tenemos dos opciones:
-
- Redondeamos: Si la cifra de la siguiente posición es menor que
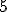, nos quedaos con las cifras del número hasta la posición que hemos escogido. Si la cifra de la siguiente posición es mayor o igual que 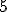, nos quedamos con las cifras del número hasta la posición que hemos escogido, pero cambiamos la cifra de esa última posición por ella misma más 
.
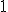- Redondeamos: Si la cifra de la siguiente posición es menor que
o
-
- Truncamos: Nos quedamos con las cifras del número hasta la posición escogida.
Como ves, truncar es cortar el número a partir de una posición, mientras que redondear supone tener en cuenta la cifra siguiente, lo que hace que los errores por redondeo sean menores o iguales que los errores por truncamiento.
En la siguiente tabla puedes ver varias aproximaciones por redondeo y truncamiento para el número irracional 
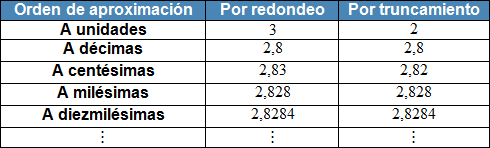
Como comentamos anteriormente, es importante controlar el error que estamos dispuestos a cometer con una aproximación. Para hacerlo se utilizan dos medidas del error:
DEFINICIÓN Dado un número y su aproximación:
- Llamamos error absoluto a:
- Llamamos error relativo a:
La diferencia entre un error y otro es que el segundo tiene en cuenta el tamaño del número en cuestión. No es lo mismo cometer un error de centímetros para un valor expresado en kilómetros que para un valor expresado en metros, por ejemplo.
¿Cuál es el problema? Pues que conocer el valor es exacto es imposible en muchos casos. Lo que se hace acotar el error, es decir, se establecen unos umbrales que no se pueden sobrepasar. Sin embargo, no es contenido de 2º ESO, así que de momento tendrás que conformarte con saber aproximar.
Notación científica
Vamos a usar todo lo que sabemos de decimales, potencias y fracciones para... ahorrar. En concreto, para ahorrar tiempo y espacio. En muchas ocasiones lo haces de forma intuitiva. Si te preguntan por tu altura, por ejemplo, lo normal es que respondas dando una medida en metros. Si consultas la duración de una película en la cartelera, aparecerá en horas o minutos, pero no en milésimas de segundo...
En otras situaciones, al trabajar con números muy grandes o muy próximos a cero, ni siquiera un cambio de unidades puede ayudarnos. Por ejemplo, la distancia media de la Tierra al Sol es de unos 
millones de kilómetros, pero sería más razonable escribirlo de otra manera:
¿No te parece mucho más cómodo? Simplemente añadimos una potencia de 
, que representa lo mismo que toda esa colección de ceros.
Para números muy próximos al cero también funciona. Por ejemplo, la carga de un electrón es aproximadamente 
coulomb y su masa 
. Ahora los exponentes de son negativos. Eso quiere decir que los ceros no están a la izquierda de la coma decimal, sino a su derecha. Para el primer número tendríamos 
ceros después de la coma y en la posición 
estaría el , seguido del 
.
Los tres anteriores son ejemplos de números expresados en notación científica, que es simplemente una forma abreviada de escribir números muy grandes o muy próximos a cero.
NOTACIÓN Un número escrito en notación científica está formado por el producto de un número decimal y una potencia de base , de manera que:
- El número decimal es mayor o igual que 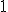y menor que .
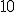- La potencia de base 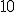tiene exponente entero.
Además de ser una notación muy cómoda, es posible operar con números escritos de esta forma con mucha facilidad. Será el próximo curso cuando aprenderás a realizar dichas operaciones. De momento nos limitaremos a usarla como expresión abreviada de ciertos números.
Ejercicio
Expresa los siguientes números en notación científica.
 |
 |
|
 |
|
|
|||||
 |
|
|
 |
|
|
|||||
 |
|
|
 |
|
|
|||||
 |
|
|
 |
|
|