Números decimales y su representación
¿Qué es un número decimal?
A estas alturas es muy posible que tengas claro lo que es un número decimal, pero haremos un pequeño repaso para curarnos en salud.
El sistema de numeración decimal es un sistema posicional de representación de números basado en potencias de 
(base ). Así dicho puede parecerte una abstracción matemática de primer nivel, pero en realidad es una idea muy simple, a la que estás totalmente acostumbrado.
Piensa, ¿cuántos símbolos distintos usas para representar cualquier número entero? Sólo diez: 
, 
, 
, 
, 
, 
, 
, 
, 
y 
. No hay más. ¿Y cómo es que arreglas con tan pocos símbolos? Pues porque la posición que ocupe una cifra en un número es muy importante. No es lo mismo 
que 
, aunque se usen los mismos símbolos. En el primer número el no indica simplemente , sino dos grupos de o, mejor dicho, dos decenas, cada una de ellas formada por unidades. Ahí es donde aparecen las potencias de del párrafo anterior.
¿Mejor así? La regla es muy sencilla, una unidad de cualquier orden se divide en diez unidades del orden inmediatamente inferior. Vamos a recordar el nombre de alguna de esas posiciones:
unidades forman una decena.
decenas forman una centena.
centenas forman una unidad de millar.
unidades de millar forman una decena de millar.
Con esto presente, podemos descomponer los número enteros en sumas de la siguiente forma:
¿Ves las potencias de ? Podríamos hacer lo mismo con cualquier entero.
OBSERVACIÓN No confundas esto con la descomposición en factores primos. SON COSAS DIFERENTES.
De momento sólo estamos hablando de números enteros, pero podemos usar también potencias de para incluir posiciones decimales. ¿Qué potencias de ? Las de exponente negativo (puedes repasar la en el bloque anterior de esta misma unidad). Al añadir estas potencias, el cuadro de unidades anterior quedaría de la siguiente forma:
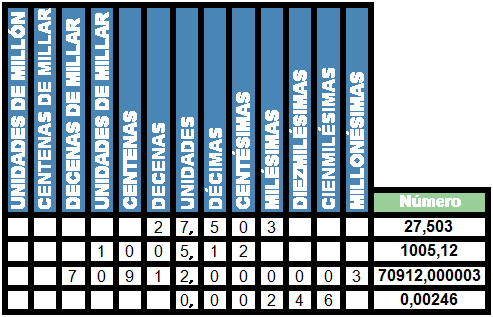
décimas forman una unidad.
centésimas forman una décima.
milésimas forman una centésima.
Ahora podemos descomponer los números decimales en sumas de la siguiente forma:
Ahí puedes ver las potencias de de exponente negativo.
OBSERVACIÓN Podemos descomponer un número decimal en dos piezas: Un número entero (parte entera) y una fracción que tenga por denominador una potencia de (parte decimal). En la práctica, llamaremos parte entera a la que está antes de la coma y parte decimal a la que está después.
Ejercicio 1
Completa la siguiente tabla:
| NÚMERO | CM | DM | UM | C | D | U, | d | c | m | dm | cm | mm |
 |
||||||||||||
 |
||||||||||||
 |
||||||||||||
 |
Ejercicio 2
Completa las siguientes frases:
a) 
unidades y una
.
b) 
unidades y ochenta y nueve mil tres
.
c) 
unidades y dos
.
d) 
unidades y trescientas sesenta y siete
.
¿Cómo se representan los decimales en la recta?
La idea es muy sencilla. Entre dos números enteros consecutivos hay una unidad completa. Si queremos representar un número decimal cuya última posición decimal sea la de las décimas, tendremos que dividir el espacio entre los enteros que correspondan en partes. Para las centésimas, en 
partes, para milésimas, 
partes...
¿Y cómo comparamos dos números decimales?
ALGORITMO Dados dos números decimales:
- Si tienen partes enteras diferentes, es mayor el que tiene mayor parte entera.
- Si tienen la misma parte entera, localizamos la primera posición decimal en la que tengan cifras diferentes, empezando a comprobar desde la coma hacia la derecha.
- Si son positivos, es mayor el que tiene la mayor de esas dos cifras.
- Si son negativos, es mayor el que tiene la menor de esas dos cifras.
Por ejemplo:
OBSERVACIÓN Los números decimales "completan" la recta numérica, es decir, para cada punto de la recta hay un número decimal y para cada decimal hay un punto de la recta. Además, entre dos números decimales cualesquiera hay infinitos números decimales.
Ejercicio 3
Completa con 
o 
:
 |
 |
 |
 |
|||
 |
 |
 |
 |
|||
 |
 |
 |
 |
|||
 |
 |
 |
 |
Utiliza el siguiente applet de Geogebra para representar números decimales.
Introduce un número en la casilla de entrada que pone "Número decimal" e intenta desplazar el punto rojo sobre la recta hasta colocarlo en la posición que has introducido.
Utiliza un punto para separar la parte entera de la decimal, no una coma.
Para mover el punto debes tener seleccionada la opción 
.
Para hacer zoom puedes pulsar ctrl y + en tu teclado (ctrl y - para quitarlo). También podrías hacerlo con la rueda del ratón.
Si necesitas desplazarte por la vista gráfica de Geogebra, debes tener seleccionada la opción 
.
¿Cuántos tipos de decimales existen?
Al trabajar con números decimales nos podemos encontrar con varios tipos diferentes. En la siguiente tabla encontrarás todas las posibilidades y algunos ejemplos.
|
DECIMALES EXACTOS |
DECIMALES NO EXACTOS | ||
 |
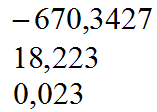PERIÓDICOS | NO PERIÓDICOS | |
| PUROS | MIXTOS |  |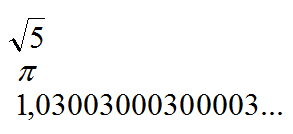
|
 |
 |
||
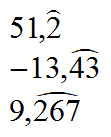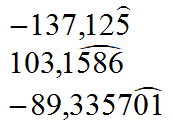DEFINICIÓN
- Los decimales exactos tienen una cantidad finita de cifras decimales (a partir de una determinada posición, todas las siguientes, hacia la derecha, son cero).
- Los decimales periódicos tienen una cantidad infinita de cifras decimales y un conjunto de esas cifras se repite de forma periódica (la misma secuencia una y otra vez hasta el infinito).
- Los periódicos puros sólo tienen parte decimal periódica.
- Los periódicos mixtos tienen parte decimal no periódica y parte decimal periódica.
- Los decimales no exactos y no periódicos tienen una cantidad infinita de cifras decimales, pero ningún conjunto de esas cifras se repite de forma periódica.
OBSERVACIÓN
- Cuando haya parte decimal periódica, ésta se marcará con el símbolo
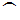encima de los números que la formen. - Puede que los ejemplos de números decimales no exactos y no periódicos te resulten algo más confusos... Insistiremos en ellos cuando relacionemos los decimales y las fracciones.
Piensa...
¿Por qué no es periódico el número 
?