Probemas
No todo van a ser cuentas...
OBSERVACIÓN Cuando te enfrentes a un problema de matemáticas (o de otra materia).
- Lee el enunciado con tranquilidad. Es importante que entiendas lo que pone. La información no está expuesta de manera directa como en un ejercicio de cálculo, hay que encontrarla entre el texto.
- Localiza la pregunta o preguntas que tengas que resolver. Es importante saber qué es lo que te pide el problema, si no, difícilmente podremos preparar una estrategia.
- Ordena toda la información útil que te da el problema para resolver la pregunta que te plantea. No todos los datos tienen por qué ser necesarios para llegar a una respuesta.
- A la hora de seguir una estrategia u otra, sería interesante estudiar si los datos que tienes te permiten aplicarla, si va a ser eficiente para el problema que tienes entre manos... pero no es obligatorio acertar a la primera. Al principio puede parecer difícil escoger "por dónde tirar", pero la práctica te dará soltura. Muchos problemas se parecen entre ellos. De hecho es algo "muy matemático" intentar utilizar estrategias que han funcionado previamente para solucionar problemas nuevos.
- Si llegas a una respuesta, comprueba que tiene sentido. No sería la primera vez que alguien dice que "Pedro tiene
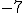años"...
Los problemas que aquí se proponen están pensados para que trabajes con ellos en tu libreta y luego compruebes la respuesta que has obtenido.
Problema 1
De los vecinos del bloque de Carmen, 
son de la provincia de A Coruña y la cuarta parte de éstos son de Melide. Si sabemos que hay seis vecinos de Melide. ¿Cuántos vecinos hay en el bloque de Carmen?
RESPUESTA: En el bloque de Carmen hay vecinos.
Problema 2
de las alumnas de 2º ESO hacen el camino de casa al colegio en coche o en autobús, mientras que las demás van andando. Si tres cuartas partes de las alumnas que usan vehículo hacen el viaje en coche y 9 alumnas utilizan autobús, ¿cuántas alumnas hay en 2º ESO?
RESPUESTA: En 2º ESO hay alumnas.
Problema 3
Entre tres hermanos deben repartirse 
€. El primero se lleva 
del total, el segundo 
del total y el tercero el resto. ¿Qué fracción del total se lleva el tercero? ¿Cuánto dinero se ha llevado cada uno?
RESPUESTAS:
| El tercero se lleva |
|
del total. |
El primero se lleva €, el segundo, € y el tercero €.
Problema 4
En un quiosco se han vendido a lo largo de la mañana los 
de un lote de periódicos. Por la tarde se ha vendido la mitad de los que habían sobrado. ¿Qué fracción del total de periódicos representan los vendidos por la tarde? Si son 20 periódicos los que no se han vendido, ¿cuántos había al empezar el día?
RESPUESTAS:
| Los periódicos vendidos por la tarde representan |
|
del total. |
Al empezar el día había periódicos.
Problema 5
Un recipiente está lleno de agua hasta los 
de su capacidad. Se saca la mitad del agua que contiene. ¿Qué fracción de la capacidad del recipiente se ha sacado? Si la capacidad del recipiente es de 
litros, ¿cuántos litros quedan en el mismo?
RESPUESTAS:
| Se han sacado |
|
de la capacidad total del recipiente. |
Quedan litros en el recipiente.
Problema 6
Una persona sale de compras. Gasta 
de su dinero en el supermercado; después 
de lo que le queda en una tienda de regalos y, finalmente, de lo restante en una librería. Si le quedan 
€, ¿cuánto dinero tenía al salir de casa?
RESPUESTA: Al salir de casa tenía €.
Problema 7
El profesor de matemáticas corrigió el lunes 
de las libretas de un grupo de alumnos. El martes corrigió 
de las que le quedaban y dejó para el miércoles el resto de las libretas, que eran 
. ¿Cuántas libretas corrigió cada día?
RESPUESTA: El lunes corrigió libretas, el martes y el miércoles .
Problema 8
A Julia le han regalado un pack en DVD con todos los episodios de la serie de televisión Perdidos. Esta primavera ha visto la tercera parte de los episodios. Durante el verano vio 
de los que le quedaban y en otoño vio los 
episodios restantes. ¿Cuántos capítulos tiene la serie?
RESPUESTA: La serie tiene capítulos.