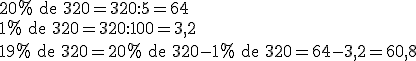Interpretaciones de un porcentaje
¿Qué son los porcentajes y cómo los calculamos?
![]() DEFINICIÓN Un porcentaje es la razón entre un número y el 100. La representación habitual consiste en escribir dicho número seguido del símbolo %.
DEFINICIÓN Un porcentaje es la razón entre un número y el 100. La representación habitual consiste en escribir dicho número seguido del símbolo %.
Por ejemplo, el porcentaje ![]() representa la razón
representa la razón ![]() .
.
La comparación con el 100 hace que la relación entre los dos números tenga una interpretación más sencilla, pero no es un concepto nuevo, sino un caso particular de las proporciones, que trabajamos en la primera parte de la unidad.
Igual que cualquier razón, podríamos interpretar un porcentaje como una fracción o un número decimal, motivo por el cuál tendremos varias opciones a la hora de calcularlos. Fíjate en el siguiente ejemplo:
El 70% de los alumnos de 2ª ESO A ha terminado el juego Thomas was alone durante las vacaciones. Si en clase hay 30 alumnos en total, ¿cuántos han completado el juego?
Podemos resolverlo de varias formas:
| COMO PROPORCIÓN | |||||||||||||
|
|||||||||||||
| COMO FRACCIÓN | |||||||||||||
| COMO NÚMERO DECIMAL | |||||||||||||
![]() OBSERVACIÓN
OBSERVACIÓN
- Las reglas de tres asociadas a los porcentajes son siempre DIRECTAS.
- Las cuentas son las mismas en los tres casos, sólo cambia la forma en que las interpretamos.
![]()
![]()
![]() Calcula:
Calcula:
![]() Completa la siguiente tabla. Simplifica las fracciones tanto como sea posible.
Completa la siguiente tabla. Simplifica las fracciones tanto como sea posible.
| PORCENTAJE | 35% | 95% | 15% | ||||||||||||||||||||||||
| FRACCIÓN |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| NÚMERO DECIMAL | 0,18 | 0,13 | 1,35 |
![]()
![]()
![]() Calcula el número al que se aplica el porcentaje en cada uno de los apartados.
Calcula el número al que se aplica el porcentaje en cada uno de los apartados.
![]()
![]()
![]() Calcula el porcentaje en cada uno de los apartados.
Calcula el porcentaje en cada uno de los apartados.
En el segundo ejercicio de esta página tienes que encontrar la fracción irreducible asociada a algunos porcentajes. Para algunos porcentajes esa fracción es muy sencilla, lo que nos permite simplificar las cuentas e incluso hacerlas mentalmente. Fíjate en los siguientes porcentajes:
- La fracción asociada al
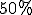 es
es 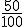 , cuya fracción irreducible es
, cuya fracción irreducible es 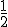 . Por tanto, para calcular el
. Por tanto, para calcular el 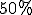 basta con dividir entre
basta con dividir entre 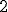 .
.
Ejemplo:
![]()
- La fracción asociada al
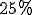 es
es 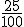 , cuya fracción irreducible es
, cuya fracción irreducible es 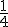 . Por tanto, para calcular el
. Por tanto, para calcular el 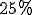 basta con dividir entre
basta con dividir entre 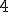 .
.
Ejemplo:
![]()
- La fracción asociada al
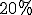 es
es 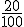 , cuya fracción irreducible es
, cuya fracción irreducible es 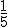 . Por tanto, para calcular el
. Por tanto, para calcular el 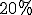 basta con dividir entre
basta con dividir entre 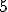 .
.
Ejemplo:
![]()
- La fracción asociada al
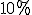 es
es 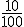 , cuya fracción irreducible es
, cuya fracción irreducible es 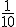 . Por tanto, para calcular el
. Por tanto, para calcular el 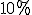 basta con dividir entre
basta con dividir entre 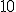 .
.
Ejemplo:
![]()
Otros porcentajes no tienen la fracción irreducible asociada tan sencilla. ¿Qué harías en esos casos? ¿Se te ocurre alguna estrategia para calcular de cabeza el ![]() ? ¿Y el
? ¿Y el ![]() ?
?