AMPLIACIÓN: Raíces de otros índices

Ejercicio 1

icono_ordenador Completa los huecos para que las igualdades tengan sentido. En los que puedas escoger, utiliza signo positivo para la base.

a) 4=16 c) 7=-1 e) 6=1000000 g) 5=-100000
b) 3=125 d) 7=-128 f) 5=243 h) 4=256
  

¿Hay raíces que no sean cuadradas?

En el caso de las raíces cuadradas, el índice (el papel que juega el exponente en las potencias) era 2, pero la misma idea se puede aplicar, como hemos visto en el ejercicio anterior, a índices diferentes. Por tanto, en general:

Definición DEFINICIÓN Llamamos raíz n-esima de un número a a un número b tal que la potencia n-ésima de b coincide con a, es decir:

\sqrt[n]{a}=b \begin{verbatim} si \end{verbatim} b^n =a

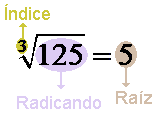
dibujo_raiz

Ejercicio 2

icono_libreta Escribe los ejemplos del ejercicio anterior con la notación que acabamos de ver e intenta adaptar la definición previa al caso de la raíz cúbica (índice 3).

Ejercicio 3

icono_ordenador Resuelve las siguientes raíces exactas. En los que puedas escoger, utiliza signo negativo para el resultado.

a) \sqrt[3]{-8}=  c) \sqrt[6]{1000000}=  e) \sqrt[4]{81}=  g) \sqrt[3]{27}= 
b) \sqrt[5]{1}=  d) \sqrt[9]{-512}=  f) \sqrt[6]{-1}=  h) \sqrt[7]{-1}= 
  

¡Cuidado con el signo del radicando!

Como puedes ver en el ejercicio anterior, los posibles resultados de una raíz varían según sea par o impar el índice. El "problema" viene con las raíces de índice par, ya que no es posible multiplicar un número por sí mismo un número par de veces y conseguir un resultado negativo.

En la siguiente tabla tienes un resumen de todas las situaciones, según sea el índice y el radicando.

Índice Radicando Número de raíces Ejemplos
Impar Cualquiera Una raíz (del mismo signo que el radicando) \sqrt[3]{27}=3, \sqrt[3]{27}=3
Par Positivo Dos raíces (positiva y negativa) \sqrt[4]{16}=\pm 2, \sqrt{25}=\pm 5
Nulo Una raíz, el 0 \sqrt[n]{0}=0
Negativo NINGUNA RAÍZ \sqrt[4]{-16} no existe