Propiedades de las potencias
¿Qué tienen de bueno las potencias?
Vale, las potencias nos permiten expresar de forma abreviada ciertas multiplicaciones, pero, ¿es eso todo?. Si tuviésemos que hacer operaciones con ellas, lo ideal sería no tener que calcularlas previamente, sino partir de varias potencias operadas entre sí y llegar a otra potencia que sea el resultado final, sin necesidad de recurrir a las operaciones "normales" con enteros.
Pues bien, gracias a la propia definición de las potencias, podremos hacer ciertas operaciones entre ellas con mucha facilidad.
![]() ALGORITMO
ALGORITMO
| Situación | ¿Qué hacemos? | Expresión simbólica | Ejemplo | IMPORTANTE |
| Multiplicación de potencias con la misma base. | Sumamos los exponentes. | |
|
La base no cambia. |
| División de potencias con la misma base. | Restamos los exponentes. | |
|
La base no cambia. |
| Potencia de una potencia. | Multiplicamos los exponentes. | |
|
La base no cambia. |
| Multiplicación de potencias con el mismo exponente. | Multiplicamos las bases. | |
|
El exponente no cambia. |
| División de potencias con el mismo exponente. | Dividimos las bases. | |
|
El exponente no cambia. |
![]() OBSERVACIÓN Las potencias de la misma base "funcionan bien" cuando las multiplicamos o dividimos, pero...
OBSERVACIÓN Las potencias de la misma base "funcionan bien" cuando las multiplicamos o dividimos, pero...
¡NO PASA LO MISMO CON LAS SUMAS Y RESTAS!
Fíjate en el siguiente ejemplo:
![]()
![]()
Como ves, son operaciones con resultados distintos. En general:
![]()
![]()
Vídeotutorial
En el siguiente videotutorial puedes ver que las propiedades de las potencias son consecuencia directa de las propiedades de la multiplicación.
¿Tiene sentido una potencia con exponente ![]() ?
?
![]() Utiliza las propiedades anteriores para expresar cada uno de los apartados como una única potencia. No utilices paréntesis en las bases.
Utiliza las propiedades anteriores para expresar cada uno de los apartados como una única potencia. No utilices paréntesis en las bases.
| a) |
f) |
||||
| b) |
g) |
||||
| c) |
h) |
||||
| d) |
i) |
||||
| e) |
j) |
¡Presta atención!
Las propiedades de las potencias son muy útiles, pero pueden llevar a confusión cuando aparecen signos "bailando" por el medio. La mayor parte de las veces el error es consecuencia de querer hacer demasiadas cosas a la vez. Si tienes dos problemas, uno de ellos el signo, y el otro usar bien las propiedades de las potencias, ¿no será mejor atender a cada uno de ellos por separado?
Es posible que al intentar resolver el ejercicio anterior hayas pensado "¿Por qué no pone paréntesis aquí?", "¿por qué éste da positivo si las dos potencias de partida son negativas?"
Mi recomendación es que primero "averigües" el signo que tendrá el resultado final y que luego apliques la propiedad de las potencias que corresponda. Así evitas problemas con el signo, porque resuelves ese "asunto" nada más empezar.
Si tengo, por ejemplo, la siguiente expresión:
![]()
La primera potencia tiene exponente par, así que su signo es positivo, mientras que la segunda tiene exponente impar, así que su signo es negativo. Por tanto, por la regla de los signos, como ![]() , el signo de la potencia resultante será negativo. Entonces, podríamos escribir:
, el signo de la potencia resultante será negativo. Entonces, podríamos escribir:
![]()
Finalmente, usando las propiedades de las potencias, el resultado final sería:
![]()
No es obligatorio atender primero al signo y luego a las potencias, de hecho, podríamos proceder del siguiente modo:
![]()
De esta forma, lo que haríamos primero sería usar una de las propiedades de las potencias y luego ocuparnos del signo. Decide tú en qué orden quieres hacerlo, pero ten en cuenta que tienes que prestar atención a las dos cosas, al signo y a las potencias.
¿Sigues sin saber por qué ![]() es positivo y
es positivo y ![]() es negativo?
es negativo?
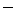 son
son