Magnitudes inversamente proporcionales
¿Que son magnitudes inversamente proporcionales?
Imagina la siguiente situación:
Al llegar el final de la primera evaluación el tutor y sus alumnos deciden organizarse para dejar la clase lo más ordenada que se pueda. Si participan los ![]() alumnos y el profesor, la clase quedaría lista en
alumnos y el profesor, la clase quedaría lista en ![]() horas. ¿Qué crees que pasará con el tiempo necesario para ordenar la clase si varía el número de personas implicadas?
horas. ¿Qué crees que pasará con el tiempo necesario para ordenar la clase si varía el número de personas implicadas?
En este caso hay dos magnitudes relacionadas; por un lado la cantidad de personas que ordenan la clase y por otro lado el tiempo (medido en horas). La relación entre ellas está determinada por las ![]() horas que tardan en recoger
horas que tardan en recoger ![]() personas. A partir de esa pareja de valores podemos saber el tiempo que tardaría en ordenar cualquier cantidad de personas.
personas. A partir de esa pareja de valores podemos saber el tiempo que tardaría en ordenar cualquier cantidad de personas.
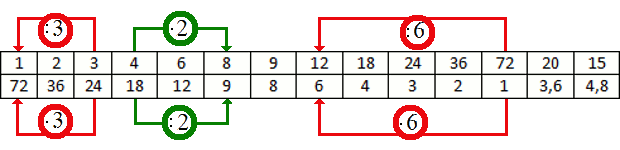
Fíjate en la siguiente tabla:
 |
|
| TIEMPO (horas) | |
| PERSONAS | |
Como puedes ver, al multiplicar una magnitud por un número, la otra resulta dividida por ese mismo número. Lo mismo sucede si dividimos.
![]() DEFINICIÓN Dos magnitudes se dicen inversamente proporcionales si al multiplicar (dividir) una de ellas por un número distinto de cero, la otra resulta dividida (multiplicada) por ese mismo número.
DEFINICIÓN Dos magnitudes se dicen inversamente proporcionales si al multiplicar (dividir) una de ellas por un número distinto de cero, la otra resulta dividida (multiplicada) por ese mismo número.
Gracias a esta característica, si conocemos un par de valores de dos magnitudes inversamente proporcionales, podemos calcular cualquier otro par. Además, las tablas de proporcionalidad inversa tienen otra característica importante:
![]() OBSERVACIÓN Dadas dos magnitudes inversamente proporcionales, la multiplicación de cualquier par de valores correspondientes da el mismo resultado. A ese producto se le llama constante de proporcionalidad inversa.
OBSERVACIÓN Dadas dos magnitudes inversamente proporcionales, la multiplicación de cualquier par de valores correspondientes da el mismo resultado. A ese producto se le llama constante de proporcionalidad inversa.
En el siguiente applet tienes la representación gráfica de la relación entre las dos magnitudes del ejemplo. Si modificas el valor de ![]() (personas que recogen el aula) verás como varía la otra magnitud (tiempo necesario para recoger). ¿Qué dibujo forman los distintos pares de valores?
(personas que recogen el aula) verás como varía la otra magnitud (tiempo necesario para recoger). ¿Qué dibujo forman los distintos pares de valores?
¿Cómo resolvemos un problema de proporcionalidad inversa?
Para resolver un problema de proporcionalidad inversa podemos seguir varios caminos diferentes. Fíjate en las distintas formas de llegar a la solución para el siguiente ejemplo.
Imagina la siguiente situación: En el instituto hay clase por la tarde cuatro días a la semana y en la cafetería se ofrece un menú para que alumnos y profesores. En estos momentos hay comida suficiente para ofrecer menú a ![]() personas por
personas por ![]() días. ¿Cuántos días se podría ofrecer menú si comiesen
días. ¿Cuántos días se podría ofrecer menú si comiesen ![]() personas diariamente? ¿Y si fuesen
personas diariamente? ¿Y si fuesen ![]() personas?
personas?
![]() ALGORITMO SOLUCIÓN POR REDUCCIÓN A LA UNIDAD
ALGORITMO SOLUCIÓN POR REDUCCIÓN A LA UNIDAD
Este método consiste en encontrar el valor que corresponde a la unidad de una de las dos magnitudes, ya que si conocemos ese par de valores es muy sencillo calcular cualquier otra pareja.
En el ejemplo que nos ocupa, como sabemos que hay comida para ofrecer menú a ![]() personas por
personas por ![]() días. No tenemos más que multiplicar por
días. No tenemos más que multiplicar por ![]() para saber la cantidad de días que se podría ofrecer menú a
para saber la cantidad de días que se podría ofrecer menú a ![]() persona. Recuerda que son magnitudes inversamente proporcionales y dividimos el número de personas entre
persona. Recuerda que son magnitudes inversamente proporcionales y dividimos el número de personas entre ![]() , así que tenemos que multiplicar el número de días por
, así que tenemos que multiplicar el número de días por ![]() .
.
![]()
Por tanto, podemos ofrecer menú a ![]() personas durante
personas durante ![]() días y a
días y a ![]() personas durante
personas durante ![]() días
días
![]() ALGORITMO SOLUCIÓN POR REGLA DE TRES INVERSA
ALGORITMO SOLUCIÓN POR REGLA DE TRES INVERSA
Ten mucho cuidado con este método. Los pares de valores de magnitudes inversamente proporcionales NO FORMAN UNA PROPORCIÓN tal y como las definimos en la primera sección de la unidad. LOS COCIENTES NO SON CONSTANTES. Lo que son constante son los productos, como comentábamos en una observación anterior.
No podemos plantear reglas de tres como en el caso de las magnitudes directamente proporcionales. En este caso las reglas de tres son INVERSAS, es decir, tendríamos que invertir las posiciones de los miembros de una de las parejas que comparemos. En la práctica, en lugar de hacer productos cruzados, los haremos "en línea".
Escribiremos:
![]()
La I que está al lado de la llave es simplemente para indicar que es una regla de tres inversa y diferenciarla de las reglas de tres directas.
En nuestro ejemplo usaremos dos reglas de tres inversas, una par calcular los días que podemos ofrecer menú a ![]() personas y otra para
personas y otra para ![]() personas:
personas:
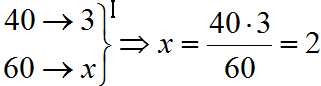 |
días | 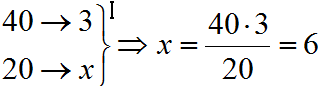 |
días |
![]() ALGORITMO SOLUCIÓN MEDIANTE LA CONSTANTE DE PROPORCIONALIDAD INVERSA
ALGORITMO SOLUCIÓN MEDIANTE LA CONSTANTE DE PROPORCIONALIDAD INVERSA
Este método consiste en calcular la constante de proporcionalidad inversa multiplicando la pareja de valores que conocemos. Una vez calculada la constante basta con dividirla entre un valor de la magnitud correspondiente para encontrar el valor de la otra magnitud asociado.
La pareja de valores que conocemos en nuestro ejemplo es ![]() personas y
personas y ![]() días, así que la constante de proporcionalidad inversa es:
días, así que la constante de proporcionalidad inversa es:
![]()
Ahora, para calcular los días correspondientes a ![]() y
y ![]() personas sólo tenemos que dividir la constante entra cada uno de esos valores. Por tanto, si comen
personas sólo tenemos que dividir la constante entra cada uno de esos valores. Por tanto, si comen ![]() personas podríamos ofrecer menú
personas podríamos ofrecer menú ![]() días y si comen
días y si comen ![]() personas,
personas,![]() días.
días.
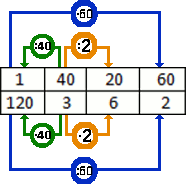
![]() OBSERVACIÓN Las cuentas son exactamente las mismas para cualquiera de las tres opciones. La única diferencia es cómo interpretar dichas cuentas. Otra estrategia válida es incluir los datos conocidos y las incógnitas en una tabla de proporcionalidad inversa y utilizar las propiedades que conocemos para calcular lo que se nos pide:
OBSERVACIÓN Las cuentas son exactamente las mismas para cualquiera de las tres opciones. La única diferencia es cómo interpretar dichas cuentas. Otra estrategia válida es incluir los datos conocidos y las incógnitas en una tabla de proporcionalidad inversa y utilizar las propiedades que conocemos para calcular lo que se nos pide:
 |
|
| PERSONAS | |
| DÍAS | |
¿Cómo detectamos una relación de proporcionalidad entre magnitudes?
Las relaciones de proporcionalidad son un tipo concreto de relación entre magnitudes, pero existen muchas más. En general, cuando queramos describir una relación entre magnitudes (variables) utilizaremos funciones, que pueden ser de muchos tipos (las estudiaremos en unidades posteriores), pero de momento nos conformaremos con identificar sólo proporciones directas e inversas.
¿Cómo hacemos para comprobar si existe una relación de proporcionalidad entre dos magnitudes?
![]() ALGORITMO Para comprobar si existe relación de proporcionalidad entre dos magnitudes multiplicamos una de las magnitudes por un número distinto de cero y comprobamos qué sucede con la otra:
ALGORITMO Para comprobar si existe relación de proporcionalidad entre dos magnitudes multiplicamos una de las magnitudes por un número distinto de cero y comprobamos qué sucede con la otra:
- Si le sucede lo mismo (resulta multiplicada por el mismo número), diremos que son directamente proporcionales.
- Si le sucede lo inverso (resulta dividida por ese número) diremos que son inversamente proporcionales.
- Si no sucede ninguna de las dos cosas, no habrá relación de proporcionalidad, aunque pueda existir otro tipo de relación.
![]() OBSERVACIÓN Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar una de ellas, aumenta la otra o que son inversamente proporcionales si al aumentar una de ellas, disminuye la otra. No es exactamente así. No es suficiente con que aumente o disminuya la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos una, multiplicamos la otra o si multiplicamos una, dividimos la otra.
OBSERVACIÓN Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar una de ellas, aumenta la otra o que son inversamente proporcionales si al aumentar una de ellas, disminuye la otra. No es exactamente así. No es suficiente con que aumente o disminuya la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos una, multiplicamos la otra o si multiplicamos una, dividimos la otra.
Piensa en la relación entre el número de aprobados y el número de suspensos en un grupo de ![]() alumnos. Si aumenta el número de aprobados, lógicamente, disminuye el número de suspensos, pero no son magnitudes inversamente proporcionales. Por ejemplo, si hay
alumnos. Si aumenta el número de aprobados, lógicamente, disminuye el número de suspensos, pero no son magnitudes inversamente proporcionales. Por ejemplo, si hay ![]() aprobados, necesariamente hay
aprobados, necesariamente hay ![]() suspensos, pero si multiplicamos los aprobado por
suspensos, pero si multiplicamos los aprobado por ![]() , resultarían
, resultarían ![]() aprobados y el número de suspensos no sería
aprobados y el número de suspensos no sería ![]() , sino
, sino ![]() .
.
CONCLUSIÓN: Tienes que comprobar las relaciones de proporcionalidad MULTIPLICANDO o DIVIDIENDO, no simplemente aumentando o disminuyendo.
![]() Indica si las siguientes magnitudes son directamente proporcionales (D), inversamente proporcionales (I) o no proporcionales (X).
Indica si las siguientes magnitudes son directamente proporcionales (D), inversamente proporcionales (I) o no proporcionales (X).
| a) Número de personas que alquilan un piso y dinero que paga cada una. | |
| b) Número de páginas de un libro y su precio. | |
| c) Lado de un cuadrado y su área. | |
| d) Peso de un una pieza de carne y su precio. | |
| e) Velocidad de un tren y tiempo que tarda en recorrer la distancia entre dos ciudades. | |
| f) Tiempo que caminas y distancia que recorres a una velocidad constante. | |
| g) Edad y altura de una persona. | |
| h) Número de personas que viajan en un autobús y recaudación por ese viaje. | |
| i) Distancia recorrida de una carrera y distancia que fata por recorrer | |
| j) Caudal de un grifo y tiempo necesario para llenar un recipiente. |
![]()
![]()
![]() Fíjate bien en las siguientes tablas e indica si las magnitudes son directamente proporcionales, inversamente proporcionales o no proporcionales.
Fíjate bien en las siguientes tablas e indica si las magnitudes son directamente proporcionales, inversamente proporcionales o no proporcionales.
|
|
|
|
RESPUESTAS:
Las magnitudes A y B son .
Las magnitudes C y D son .
Las magnitudes E y F son .