Medición del radio terrestre
El departamento de Matemáticas ha realizado una experiencia muy interesante en colaboración con otro instituto de Canarias. A continuación os describimos la experiencia.
1.- ERATÓSTENES DE CIRENE
El descubrimiento de que la Tierra es un mundo pequeño se llevó a cabo
en el antiguo Oriente próximo, en una época que algunos humanos llaman siglo
III a. de C.. La mayor metrópolis de aquel tiempo era la ciudad egipcia de
Alejandría.
Eratóstenes (273 a.C. 192
a.C.) se educó en Atenas, pero pasó más de la mitad de su vida en
Alejandría. Fue astrónomo, historiador, geógrafo, filósofo, poeta,
critico teatral y matemático. Fue también director de la gran Biblioteca de
Alejandría, donde un día leyó en un libro de papiro que, en un puesto
avanzado de la frontera meridional, en Siena (actualmente Assuán), cerca de la
primera catarata del Nilo, en el mediodía de junio un palo vertical no proyecta
sombra. En el solsticio de verano, el día más largo del año, a medida que
avanzaban las horas y se acercaba el mediodía las sombras de las columnas del
templo iban acortándose. En el mediodía habían desaparecido. En aquél
momento podía verse el Sol reflejado en el agua, en el fondo de un profundo
pozo. El Sol estaba directamente encima de las cabezas.
Era una observación que otros podrían haber ignorado con facilidad.
Palos, sombras, reflejos en pozos, la posición del Sol: ¿qué importancia podían
tener cosas tan sencillas y cotidianas?. Pero Eratóstenes era un científico, y
sus reflexiones sobre estos tópicos cambiaron el mundo; en cierto sentido
hicieron el mundo.
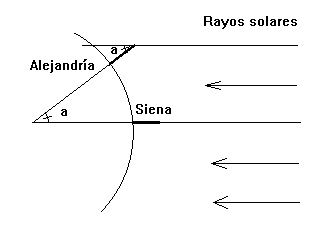
Eratóstenes observo que los palos verticales proyectaban sombra al mediodía del 21 de junio en Alejandría. Ese mismo día midió la sombra de un obelisco en Alejandría y mediante simple geometría calculó que la sombra proyectada correspondía a una desviación de los rayos del sol, respecto a la vertical, de 7º 14’. Esto correspondí a 1/50 de la circunferencia total de la Tierra (360º). La circunferencia de la Tierra debía ser igual a 50 veces la distancia que mediaba entre Siena y Alejandría. Pero, ¿cuál era esa distancia?. Él sabía, por los viajeros, que los camellos necesitaban unos 50 días para cubrirla, y que un camello recorría cien estadios en un día. La distancia entre Siena y Alejandría era de cinco mil estadios. Eratóstenes calculó que la circunferencia de la Tierra era doscientos cincuenta mil estadios. No estamos seguros de cuál es el equivalente exacto entre los estadios y los metros, pero los mejores cálculos otorgan que 1 estadio = 185 metros. El “estadio griego”, del cual proviene nuestra palabra estadio, era una carrera pedestre que tenía precisamente esa longitud.
Según
estos cálculos, Eratóstenes llegó a la conclusión de que la circunferencia
terrestre medía unos 46.190 kilómetros, cifra que sobrepasa a la medida actual
(40.074 kilómetros) en un 15 %. La importancia de este resultado, no es debida
a la exactitud de los cálculos, sino a al exactitud científica del método
utilizado, siendo la mejor estimación del radio de la Tierra hasta los tiempos
modernos.
2.-MEDICIÓN DEL RADIO DE LA TIERRA
Intentamos medir el radio de la Tierra por un procedimiento parecido al
utilizado por Eratóstenes en el siglo III
a.C.
Necesitamos
medir el ángulo con que caen los rayos del sol, con respecto a la vertical, el
mismo día, en los dos centros docentes, cuando el sol pasa por el meridiano del
lugar, es decir, a las 12 horas solares. Esto, no sucede a las doce del medio día
como podríamos suponer, ni tan siquiera sucederá a un ahora en punto, debido a
dos factores: el adelanto o retraso de los relojes en función de la época del
año para el mejor aprovechamiento de las horas de sol, y la distinta posición
de los centros docentes dentro de sus propios husos horarios.
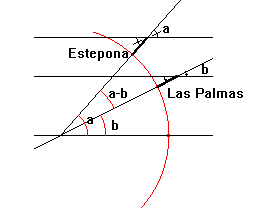
La
diferencia horaria entre los dos centros docentes no será un problema ya que al
regirse cada centro por su horario oficial, el sol pasará por el meridiano de
Estepona aproximadamente una hora antes que por el meridiano de Las Palmas, que
es precisamente la diferencia horaria de las Islas con respecto a la Península.
La
determinación de cuándo pasará exactamente el sol por el meridiano del lugar,
no va a ser necesaria que se calcule exactamente. El tiempo durante el cual se
estarán tomando medidas será, desde una hora antes de paso del sol por el
meridiano del lugar, hasta una hora después aproximadamente. A pesar de todo,
en el desarrollo de las mediciones, se puede ir anotando al lado de cada marca,
la hora a la que se realiza dicha marca, pudiendo saberse a posteriori, la hora
a la que se produjo el paso del sol por el meridiano.
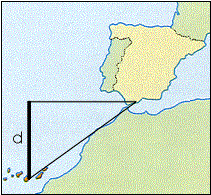
Otro
dato importante a conocer es la distancia que separa a Estepona de Las Palmas.
Esta distancia no es una distancia lineal, sino la distancia que separaría a
las dos poblaciones, si estuvieran situadas sobre el mismo meridiano. Para
calcularla necesitaremos algún mapa geográfico (mapa de España, Geológico o
de carreteras), que tenga trazada la retícula de meridianos y paralelos y en el
que conste la escala. También podríamos utilizar la diferencia de latitud de
las dos poblaciones y conociendo la longitud de la circunferencia terrestre,
hacer el correspondiente cálculo de la distancia a la que corresponde esa
diferencia de latitud. Pero como el objetivo de la práctica es el de calcular
precisamente el radio terrestre y por consiguiente la longitud de la
circunferencia terrestre, me inclino por que utilicemos el primer método y
explicar a los alumnos como podemos calcular esa distancia sobre un mapa
escalado. Como resultado podemos utilizar la media de las dos estimaciones que
hagamos por separado.
A
continuación te describo dos tipos de montajes para realizar las mediciones.
Los resultados son idénticos con los dos montajes, aunque el primero pueda
parecer más exacto. Lo ideal sería que algunos grupos utilizaran el primer
modelo y otros el segundo, pero eso lo dejo a tu elección.
2.1.-MONTAJE
EXPERIMENTAL
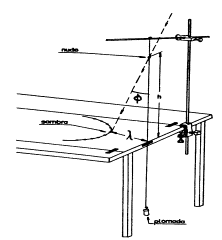
Cada
grupo de alumnos deberá hacer el siguiente montaje experimental:
·
Se sacará
al patio una mesa, que se nivelará adecuadamente, hasta que quede perfectamente
horizontal. Una simple canica que no ruede por la superficie de la mesa nos
puede indicar que está horizontal ( si es posible, lo ideal es utilizar un
nivel de albañilería). Sería conveniente que la mesa estuviera orientada,
aproximadamente, en dirección NS.
·
De una
varilla soporte se colgará una cuerda con un peso que realizará las funciones
de plomada.
·
En la parte
superior de la cuerda se realizará un nudo ( se puede utilizar una pequeña
bola de papel para que la sombra sea más distinguible), cuya sombra se
proyectará sobre una cartulina situada sobre la mesa y fijada a la mesa con
cinta adhesiva.
·
Con mucho cuidado, se
girará la varilla soporte hasta conseguir que la cuerda quede perfectamente
rasa con el borde de la mesa. Para conseguir que la plomada no se mueva de esta
posición, evitando que las corrientes de aire dificulten la toma de datos, se
fijará la cuerda al borde de la mesa con cinta adhesiva.
Cuando
se produzca la distancia mínima (
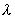) desde la marca a la base de la
plomada, el sol estará justo sobre el meridiano del lugar.
El cálculo que nos interesa, es el del ángulo
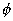, que será el ángulo que forma el sol con respecto a la vertical en ese
momento. Este ángulo lo podemos calcular utilizando la
trigonometría, mediante la fórmula:
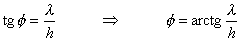
Si no se desea utilizar la trigonometría, también podríamos utilizar
el teorema de Pitágoras para calcular la hipotenusa del triángulo rectángulo
de catetos
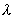y h
y por semejanza, construir un triángulo rectángulo a una escala adecuada para
medir el ángulo con un transportador de ángulos.
2.2.-MONTAJE
MEDIANTE GNOMON
Si no tenemos posibilidad de realizar un montaje del tipo de la página
anterior, podemos utilizar lo que se llama un Gnomon.
Un Gnomon, en su forma más sencilla, consta de una varilla –estilo-
situada en la dirección de la vertical del lugar, sobre una superficie plana
horizontal en la que se proyecta la sombra del estilo producida por los rayos
del sol.
En la forma más sencilla, el Gnomon sería una varilla de madera, de
cualquier medida clavada verticalmente en el suelo, o colocada verticalmente
sobre una plataforma horizontal.
El Gnomon es el antecesor de todos los instrumentos astronómicos basados
en la proyección de la sombra de un objeto y a pesar de su sencillez de
construcción, es muy grande la cantidad de información que puede proporcionar.
Por medio de él se pueden determinar: las direcciones NS y EW, la latitud del
lugar, la altura de la culminación del sol en un día, la oblicuidad de la eclíptica,
y otras aplicaciones de enorme interés astronómico.
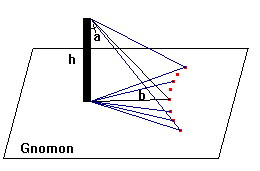
El montaje experimental consistiría en clavar una estaca sobre la arena
en posición perfectamente vertical, para poder ir marcando, en intervalos
cortos de tiempo, la punta de la sombra de la estaca. Cuando se produzca la
distancia mínima ( b ) desde la punta
de la sombra a la base de la estaca, el sol estará justo sobre el meridiano del
lugar.
El cálculo que nos interesa, es el del ángulo a,
que será el ángulo que forma el sol con respecto a la vertical en ese momento.
Este ángulo lo podemos calcular utilizando la trigonometría, mediante la fórmula:
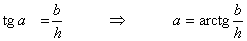
Si no se desea utilizar la trigonometría, también podríamos utilizar
el teorema de Pitágoras para calcular la hipotenusa del triángulo rectángulo
de catetos h y b
y por semejanza, construir un triángulo rectángulo a una escala adecuada para
medir el ángulo con un transportador de ángulos.
3.- DESARROLLO DE LA PRÁCTICA
Se
distribuirán los alumnos de la clase en cinco o seis grupos, para hacer en cada
centro, cinco o seis mediciones de la inclinación de los rayos solares con
respecto a la vertical y utilizar como dato real, la media de las mediciones
obtenidas. Entre las 12:15 y hasta las 13:45 se irán marcando, a intervalos de
cinco minutos, el extremo de la sombra del Gnomon. Al concluir ese periodo se
habrá producido el paso del sol por el meridiano del lugar (cuando la sombra
del Gnomon halla sido mínima). Las mediadas necesarias las podremos hacer con
posterioridad a este momento con una cinta métrica.
Con
los datos obtenidos por todos los grupos, se completará la siguiente tabla:
|
CENTRO A |
Longitud mínima de la sombra
( b ) |
Altura del Gnomon
( h ) |
Ángulo ( a
) en grados |
Ángulo ( a )
en radianes |
|
Grupo 1 |
|
|
|
|
|
Grupo 2 |
|
|
|
|
|
Grupo 3 |
|
|
|
|
|
Grupo 4 |
|
|
|
|
|
Grupo 5 |
|
|
|
|
|
Grupo 6 |
|
|
|
|
|
Valor_medio |
|
|||
Las tablas completadas por los dos centros se intercambiarán mediante
Fax, para que cada centro pueda completar los cálculos.( El último folio, es
una plantilla para completar la tabla e intercambiárnosla por Fax. )
Si consideramos que:
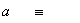Ángulo de inclinación
obtenido en Estepona.
Ángulo de inclinación obtenido en Las Palmas.
Y
utilizando la definición intuitiva de radian ( la medida del ángulo, debemos
expresarla en radianes):
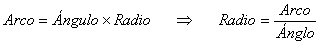
Por
lo que tendremos que:
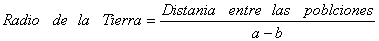
4.-TRABAJO DE LOS GRUPOS
El
desarrollo temporal y los trabajos a realizar por los alumnos serán los
siguiente:
·
La clase
anterior a la realización de al práctica, el profesor hará una exposición de
todo el proceso a seguir, suministrando a los alumnos toda la documentación
necesaria para la realización de la misma. Se resolverán las dudas que puedan
surgir, y se hará un listado del material necesario para el montaje elegido.
También se necesitará materiales como una cinta métrica, cinta adhesiva,
nivel para nivelar la mesa, tiza para marcar sobre el suelo, brújula, dos cámaras
fotográficas, dos carretes fotográficos y cualquier material que los alumnos
crean conveniente.
·
El día de
la realización de la práctica, se debe sacar al patio todo el material
necesario y realizar el montaje con anterioridad a la hora de comienzo de la
práctica. Es muy importante concienciar a los alumnos en la necesidad de
que los datos sean tomados con la mayor exactitud posible. Como aliciente para
esto, uno de los aspectos que se puntuará de la práctica será, un cálculo
previo con la medida obtenida por el grupo, y la media de las medidas obtenidas
en el otro centro. El grupo que obtenga un resultado más aproximado al real,
será el que obtenga una mayor puntuación en este apartado.
·
Cálculo de
resultados y valoración de los mismos. El día siguiente a la realización de
la práctica, se puede dedicar a que los grupos rellenen en clase el
cuestionario, haciendo un coloquio final sobre las causas del error cometido con
respecto al valor verdadero
·
Las tres
horas siguientes de clase, se dedicarán a la confección de carteles por los
grupos. Algunas de las sugerencias para los carteles pueden ser:
-
La Gran Biblioteca de Alejandría.
-
Mapa del antiguo Egipto que contenga Alejandría y Siena.
-
Vida de Eratóstenes e ilustración de su método.
-
La Astronomía en Grecia y Egipto.
-
Montaje utilizado para la medición y resultado obtenido.
-
Mapa con la situación geográfica de Las Palmas y Estepona con el método utilizado para el cálculo de la distancia.
- Carteles fotográficos
He pensado en la
confección de dos carteles fotográficos:
1.- Un primer cartel con catorce fotos, siete de cada centro,
una por cada uno
de los grupos junto con sus gnómones, y
otra de la clase
al completo. Estas fotos nos las podríamos
intercambias por
correo.
2.- Un Cartel
libre con fotografías tomadas durante la
práctica y
durante la confección de los carteles.
-
Temas propuestos por los alumnos. Etc...
·
Valoración
por parte del profesor de los resultados de la práctica.
Valoración
de aspectos teóricos de la práctica.
Valoración
de comprensión de la práctica.
Valoración
de la confección y presentación de carteles.
·
Exposición,
algún día significativo para el centro, de los carteles confeccionados.
Medición del Radio de la Tierra.
|
COMPONENTES
DEL GRUPO |
|
|
|
|
|
|
|
|
|
|
|
|
VALORACIÓN DE ASPECTOS TEÓRICOS DE LA PRÁCTICA
1.-
Cálculo previo del radio terrestre con la medida obtenida por el grupo, y la
media de las medidas obtenidas en el otro centro.
Porcentaje de error cometido con respecto al valor real
2.-
Cálculo del radio terrestre con la media de las medidas obtenidas por los dos
centro.
Porcentaje de error cometido con respecto al valor real.
3.-
Utilizando el valor obtenido para el radio terrestre, calcula:
Longitud del ecuador terrestre.
Volumen de la esfera terrestre.
Velocidad de rotación de la tierra.
4.-
¿Qué factores crees que han influido en el error obtenido?. Coméntalos en
grupo.
VALORACIÓN
DE COMPRENSIÓN DE LA PRÁCTICA.
4.-
Intenta explicar porqué el ángulo obtenido en Las Palmas es menor que el ángulo
obtenido en Estepona.
5.-
¿Qué crees que habría sucedido si hubiésemos hecho la práctica en el mes de
Junio?. Razona la respuesta.
6.-
Se podría haber hecho la práctica con dos centros que estuviesen sobre el
mismo paralelo?. Razona la respuesta.
7.-
¿Qué modificaciones tendríamos que haber hecho en los cálculos si los
centros hubiesen estado en hemisferios distintos?.
VALORACIÓN
DE LA CONFECCIÓN DE CARTELES.
8.-
Tema elegido para el cartel
9.-
Inventario del material necesario para el cartel, especificando material que
aportan los alumnos y material que debe aportar el centro.
BIBLIOGRAFÍA
ESPECÍFICA PARA
LA PRÁCTICA:
“ Curso de astronomía teórica y práctica”
Autores.: J. Fábregas, M.
García y R. Sendra
Editorial.: ECIR
“ Las medidas del Universo”
Autores.: Tomás Hormigo
Editorial.: MARFIL
“Cosmos”
Autores.: Carl Segan
Editorial.: PLANETA
“Métodos matemáticos de la ciencia”
Autores.: George Pólya
Editorial.: Revista LA
TORTUGA
ASTRONOMÍA.:
“Guía de campo de las estrellas y los planetas
del hemisferio norte y sur”
Autores.: Jay M. Pasachoff y Donald H.
Menzel
Editorial.: OMEGA
“Guía mensual del cielo”
Autores.: Ian Ridpath
y Wil Tirión
Editorial.: ALIANZA
EDITORIAL
“Experimentos de Astronomía”
Autores.: Lars Broman, R.
Estalella y Rosa Mª Ros
Editorial.: Biblioteca de
recursos didácticos Alambra
“La revolución Científica”
Autores.: Antoni Baig y
Monserrat Agustench
Editorial.: Biblioteca de
recursos didácticos Alambra
“El lenguaje secreto de las estrellas y los planetas”
Autores.: Geoffrey Cornelius
y Paul Devereux
Editorial.: DEBATE
INTERCAMBIO DE DATOS
DATOS DEL CENTRO
CENTRO.:
________________________________________
DIRECCIÓN.:
________________________________________
POBLACIÓN.:
________________________________________
TELEFONO.:
________________________
FAX.:
________________________
FECHA.:
________________________
DATOS DE LA PRÁCTICA
|
CENTRO A |
Longitud mínima de la sombra (
b ) |
Altura del Gnomon ( h
) |
Ángulo a medido en
grados |
Ángulo a
medido en radianes |
|
Grupo 1 |
|
|
|
|
|
Grupo 2 |
|
|
|
|
|
Grupo 3 |
|
|
|
|
|
Grupo 4 |
|
|
|
|
|
Grupo 5 |
|
|
|
|
|
Grupo 6 |
|
|
|
|
|
Valor
medio |
|
|||
DISTANCIA ESTIMADA ENTRE ESTEPONA Y LAS PALMAS
______________________ km.
OBSERVACIONES.:
