Algunos tipos de sucesiones (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág 58)
Progresiones aritméticas
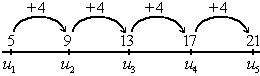
Una progresión aritmética es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija,  , que llamaremos diferencia.
, que llamaremos diferencia.
Escrito en forma recursiva:
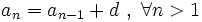
Por ejemplo, la sucesión 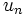 :
:
es una progresión aritmética con diferencia 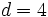 .
.
Progresiones aritméticas: definición y ejemplos.
Determina el quinto término de la siguiente progresión aritmética: {-3, -7, -11, -15, ...}
Dados los términos de una progresión aritmética, completar la fórmula de recurrencia.
Actividades en las que aprenderás el concepto de progresión aritmética y a cómo identificarlas.
Actividades de introducción a las sucesiones aritméticas.
Fórmulas recursivas para sucesiones aritméticas.
Extiende sucesiones aritméticas.
Fórmulas recursivas para sucesiones aritméticas.
Término general de una progresión aritmética
Término general de una progresión aritmética
El término general, 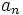 , de una progresión aritmética de diferencia
, de una progresión aritmética de diferencia  es:
es:
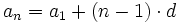
En efecto, de forma intuitiva:
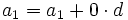
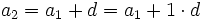
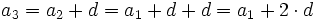
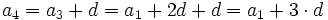
........................
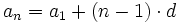
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
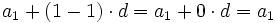
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
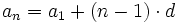 . [1]
. [1]Por ser una progresión aritmética cada término se obtiene sumando d al anterior término:
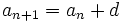 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n+ d \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 + (n-1) \cdot d + d =a_1 + ((n+1)-1) \cdot d](/wikipedia/images/math/7/4/4/744cf81c67660fb80f54db415de019dd.png)
- Definición de progresión aritmética.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones aritméticas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Término general de una progresión aritmética: Obtención y ejemplos.
Término general de una progresión aritmética: Más ejemplos
Término general de una progresión aritmética a partir de términos intermedios.
- Definición de progresión aritmética.
- Ejemplos
- Término general
- Una progresión aritmética tiene como término general
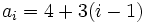 , halla el término
, halla el término 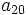 .
.
- Halla el término
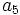 de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Halla el término general y la forma recursiva de las siguientes progresiones aritméticas:
- a) {-5, -3, -1, 1, ...}
- b) {100, 107, 114, 121, ...}
- c) {1, 3, 6, 10, ...}
Halla el término general de las siguientes progresiones aritméticas:
- a) {12, 5, -2, -9, ...}
- b) {-100, -50, 0, 50, ...}
Halla el término 100 de la siguiente progresión aritmética: {15, 9, 3, -3, ...}.
Halla la forma recursiva de la progresión aritmética con término general 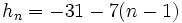
Actividad de introducción a las fórmulas de sucesiones aritméticas.
Actividad para aprender a obtener el término general (fórmula explícita) de sucesiones aritméticas.
Actividades en las que aprenderás a obtener el término general de una progresión aritmética.
Convertir formas de sucesiones aritméticas, recursivas y explícitas.
Repaso de sucesiones aritméticas.
Usa el término general de progresiones aritméticas.
Obtén el término general (fórmula explícita) de sucesiones aritméticas.
Encuentra el término general de una progresión aritmética dada.
Convertir formas de sucesiones aritméticas, recursivas y explícitas.
Suma de términos de una progresión aritmética
Suma de los "n" primeros términos de una progresión aritmética
La suma de los n primeros términos de una progresión aritmética es:
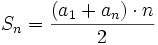
El porqué de esta fórmula se deduce de la siguiente historia:
En un pequeño pueblo de Alemania, Brunswick, un día en la escuela el profesor manda sumar los cien primeros números naturales. El maestro quería unos minutos de tranquilidad... pero transcurridos pocos segundos uno de los alumnos levanta la mano y dice tener la solución: los cien primeros números naturales suman 5.050. Y efectivamente, así era.
El profesor le preguntó ¿cómo lo has hecho? El niño le dijo: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101,... siempre suma 101 y hay 50 sumas, en total 50 * 101 = 5050. El profesor quedó tan impresionado que le regaló un libro de Aritmética.
Ese niño tenía 10 años y se llamaba Carl Friedrich Gaüss. Fue uno de los mas grandes matemáticos. Intenta enterarte de algo más sobre él.
Demostración:
Para la demostración nos basaremos en el hecho de que:
Entonces, si efectuamos la siguiente suma:
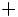
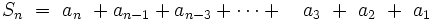
- _______________________________________________________________
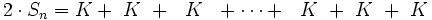
por tanto:
Actividades en las que aprenderás a obtener de los "n" primeros términos de una progresión aritmética.
Fórmula de la suma de los n primeros términos de una progresión aritmética. Ejemplos.
Fórmula de la suma de los n primeros términos de una progresión aritmética con demostración apoyada en la anécdota de Gauss. Ejemplo.
Demostración de la fórmula de la suma de los n primeros términos de una progresión aritmética
Halla el valor del ángulo θ, sabiendo que 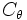 representa su complementario y
representa su complementario y 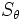 su supementario, teniendo en cuenta que se cumple la siguiente expresión:
su supementario, teniendo en cuenta que se cumple la siguiente expresión:

Suma los n primeros términos de una progresión aritmética dada.
Actividades
|
Actividad: Progresiones aritméticas Dada la sucesión {1, 4, 7, 10, 13, 16, ...}: a) Halla el término general. b) Halla el término 20. c) Halla la suma de los 20 primeros términos. d) Halla la suma de los términos del 8 al 15. d) Halla la suma de los términos del p al q. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 4, 7, 10, 13, 16, ...} b) {3n-2} for n=20 c) sum {3n-2} for n=1 to 20 d) sum {3n-2} for n=8 to 15 e) sum {3n-2} for n=p to q |
Obtención del término general y de la suma de los términos de la progresión aritmética 1, 6, 11, 16, ...
En una progresión aritmética el primer término es 6 y la diferencia 5. Halla el séptimo término.
En una progresión aritmética el primer término es -6 y el décimo término es 21. Halla la diferencia.
En una progresión aritmética el tercer término es 24 y el décimo término es 66. Halla el primer término y la diferencia.
En una progresión aritmética el segundo término es 20 y el quinto término es 56. Halla el término décimo y la suma de los diez primeros términos.
La suma de los primeros 21 términos de una progresión aritmética es 420. El décimonoveno término es cuatro veces el tercer término. Encuentra el primer término y la diferencia.
Sea 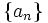 una progresión aritmética de diferencia
una progresión aritmética de diferencia 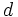 :
:
- Determina
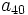 sabiendo que
sabiendo que  y
y 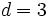 .
.
- Determina
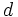 sabiendo que
sabiendo que 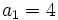 y
y 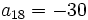 .
.
- Determina
 sabiendo que
sabiendo que 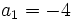 y
y 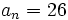 y
y 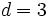 .
.
- Determina
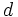 ,
, 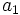 y
y  sabiendo que
sabiendo que 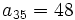 y
y 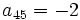 .
.
- Determina
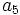 y
y 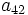 sabiendo que
sabiendo que 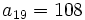 y
y 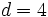 .
.
Sea 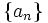 una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
Completa las siguientes igualdades:
- Sea
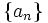 una progresión aritmética. Halla
una progresión aritmética. Halla 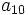 sabiendo que
sabiendo que 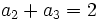 y
y 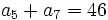 .
.
- Si las longitudes de los lados de un triángulo rectángulo están en progresión aritmética, determina el perímetro sabiendo que la hipotenusa mide 30 m.
- Determina tres números en progresión aritmética de modo que su suma sea 12 y la suma de sus cuadrados sea 16.
- Determina los lados de un triángulo rectángulo sabiendo que están en progresión aritmética de diferencia 7.
Sea 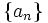 una progresión aritmética de diferencia d. Determina:
una progresión aritmética de diferencia d. Determina:
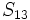 sabiendo que
sabiendo que 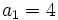 y
y 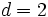 .
.
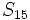 sabiendo que
sabiendo que 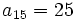 y
y 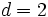 .
.
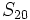 sabiendo que
sabiendo que 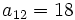 y
y 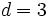 .
.
- k sabiendo que
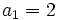 ,
, 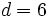 y
y 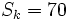 .
.
Sea 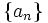 una progresión aritmética de diferencia
una progresión aritmética de diferencia 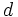 . Determina:
. Determina:
- d sabiendo que
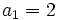 y
y 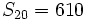
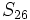 sabiendo que
sabiendo que 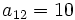 y
y 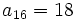 .
.
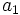 sabiendo que d=3 y
sabiendo que d=3 y 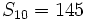 .
.
 sabiendo que
sabiendo que 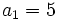 ,
, 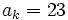 y
y 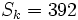 .
.
- La suma de los n primeros términos de la sucesión 3, 7, 11, ... es 210. Halla n.
- La suma de los 6 primeros términos de una progresión aritmética es 36, siendo
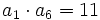 . Determina el término general de la progresión.
. Determina el término general de la progresión.
Halla el término general de una progresión aritmética cuya diferencia es 3 y cuyo quinto término es -1. calcula también la suma de los 20 primeros términos.
En una progresión aritmética se cumple que 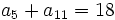 y
y 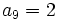 . Halla
. Halla 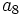 ,
, 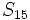 y
y  .
.
La suma de los 50 primeros términos de una progresión aritmética es 2650. Si la diferencia es 2, calcula el primer término y los términos centrales.
Ejercicios
Problemas
|
Problema: Progresiones aritméticas Al excavar tierra para hacer un túnel se pagan 700€ por el primer metro y 95€ de aumento por cada metro sucesivo (es decir, 795€ por el segundo metro,...). a) ¿Cuánto se pagará por el décimo metro excavado? b) Calcular el total abonado por los 10 metros excavados.Solución: 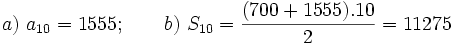 |
(Pág. 58)
Progresiones geométricas
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija,  , que llamaremos razón.
, que llamaremos razón.
Escrito en forma recursiva:
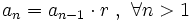
Por ejemplo, la sucesión 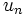 :
:
es una progresión geométrica de razón 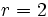 .
.
Progresiones geométricas: definición y ejemplos.
Halla el quinto término de la siguiente progresión geométrica: 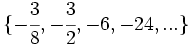
Halla el término 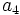 de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Actividades en las que aprenderás el concepto de progresión geométrica y a cómo identificarlas.
Extiende sucesiones geométricas.
Extiende sucesiones geométricas con términos negativos y racionales.
Fórmulas recursivas para sucesiones geométricas.
Término general de una progresión geométrica
Término general de una progresión geométrica
El término general, 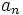 , de una progresión geométrica de razón
, de una progresión geométrica de razón  es:
es:
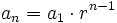
En efecto, de forma intuitiva:
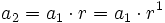

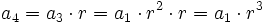
........................
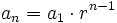
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
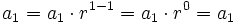
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
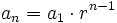 . [1]
. [1]Por ser una progresión geométrica cada término se obtiene multiplicando por r el anterior término:
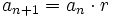 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n \cdot r \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 \cdot r^{n-1} \cdot r =a_1 \cdot r^{((n+1)-1)}](/wikipedia/images/math/b/5/0/b50e2fb51571873946095ab7579f8b90.png)
- Definición de progresión geométrica.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones geométricas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Término general de una progresión geométrica: Obtención y ejemplos.
- Definición de progresión geométrica.
- Ejemplos.
- Término general de una progresión geométrica.
Una progresión geométrica tiene como término general 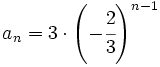 , halla el término
, halla el término 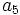 .
.
Halla el término general y la forma recursiva de la siguiente progresión geométrica: {168, 84, 42, , 21, ...}.
Halla la fórmula recursiva a partir del término general 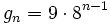 .
.
Problema sobre progresiones geométricas.
Actividades en las que aprenderás a obtener el término general de una progresión geométrica.
Progresiones geométricas.
Usa el término general de una progresión geométrica.
Halla el término general de una progresión geométrica.
Convertir formas recursivas y explícitas de sucesiones geométricas.
Problemas verbales con progresiones geométricas.
Ejercicio resuelto: Progresión geométrica
En una progresión geométrica de términos positivos, 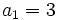 y
y 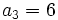 .
Halla
.
Halla  ,
, 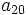 y
y 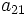 .
.
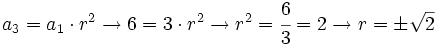
Como la progresión es de términos positivos, sólo nos vale el valor posivo: 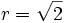 .
.
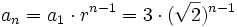
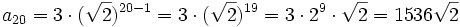
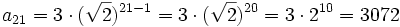
Encuentra el término general de una progresión geométrica dada.
Suma de términos de una progresión geométrica
Suma de términos de una progresión geométrica
La suma de los n primeros términos de una progresión geométrica es:
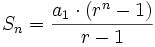
Efectuamos la siguiente resta:
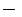
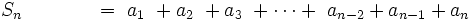
- ______________________________________________________________________________

por tanto:
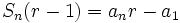
y despejando
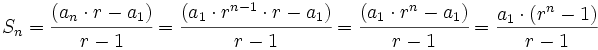
Actividades en las que aprenderás a obtener de los "n" primeros términos de una progresión geométrica.
Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.
Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.
Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
Suma los n primeros términos de progresión geométrica dada.
Ejercicio resuelto: Suma de términos de una progresión geométrica
Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año?
Se trata de un problema típico de aritmética comercial de anualidades de capitalización:
Al comenzar el primer año ingreso 1000 €, que se transforman en 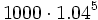 al final del quinto año.
al final del quinto año.
Al comenzar el segundo año ingreso 1000 €, que se transforman en 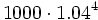 al final del quinto año.
al final del quinto año.
Al comenzar el tercer año ingreso 1000 €, que se transforman en 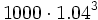 al final del quinto año.
al final del quinto año.
Al comenzar el cuarto año ingreso 1000 €, que se transforman en 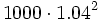 al final del quinto año.
al final del quinto año.
Al comenzar el quinto año ingreso 1000 €, que se transforman en 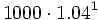 al final del quinto año.
al final del quinto año.
Si sumamos todas esas cantidades:
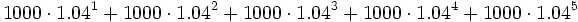
estaremos sumando los cinco primeros términos de una progresión geométrica con 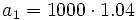 y
y 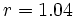
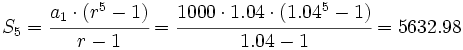 €
€Anualidades de capitalización son cantidades fijas que se entregan al principio de cada año para su colocación a interés compuesto con objeto de llegar a constituir un capital al cabo de un determinado número de años.
Anualidades de amortización son pagos fijos que se entregan al final de cada año para su colocación a interés compuesto, con objeto de llegar a extinguir o amortizar una deuda juntamente con sus intereses, en un determinado número de años.
Suma de los infinitos términos de una progresión geométrica
Suma de los infinitos términos de una progresión geométrica
La suma de todos los términos de una progresión geométrica en la que su razón verifica que 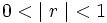 se obtiene así:
se obtiene así:
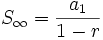
Para la demostración se requiere del concepto de límite. Véase: Algunos límites importantes.
Actividades en las que aprenderás a obtener la suma de todos los términos de una progresión geométrica, siempre que ésto sea posible.
Fórmula de la suma de todos los términos de una progresión geométrica. Ejemplos.
Fórmula de la suma de los infinitos términos de una progresión geométrica. Ejemplos.
Producto de términos de una progresión geométrica
Producto de "n" términos de una progresión geométrica
El producto de los n primeros términos de una progresión geométrica es:
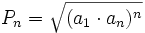
Véase en el siguiente videotutorial.
Actividades en las que aprenderás a obtener el producto de los "n" primeros términos de una progresión geométrica.
Demostración de la fórmula del producto de n términos de una progresión geométrica
Actividades
|
Actividad: Progresiones geométricas Dada la sucesión {1, 1/2, 1/4, 1/8, ...}: a) Halla el término general. b) Halla el término 10. c) Halla el producto de los 10 primeros términos. d) Halla la suma de los términos del 10 al 15. e) Halla la suma de los infinitos términos. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 1/2, 1/4, 1/8, ...} b) {2^(-n+1)} for n=10 c) product {2^(-n+1)} for n=1 to 10 d) sum {2^(-n+1)} for n=10 to 15 d) sum {2^(-n+1)} for n=1 to oo
|
Obtención del término general y de la suma de los términos de las siguientes progresiones geométricas:
- a) Dada la progresión 2, 6, 18, 54, ..., halla su término general y la suma de los 20 primeros términos.
- b) Dada la progresión 8, 4, 2, 1, ... , halla su término general y la suma de todos sus términos.
El primer término de una progresión geométrica es 3 y la razón 2. Halla el quinto término y la suma de los ocho primeros términos.
El primer término de una progresión geométrica es -4 y el sexto término es 972. Halla la razón.
El cuarto término de una progresión geométrica es 8 y el noveno término es 1/4. Halla la suma de todos los términos de la progresión.
Determina tres números en progresión geométrica de manera que su producto sea 216 y su suma 19.
- Determina la progresión geométrica tal que
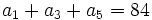 y
y 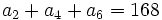 .
.
- Determina tres números en progresión geométrica de manera que su suma sea 28 y la diferencia entre el tercero y el primero sea 12.
Determina tres números en progresión geométrica de manera que al sumar 2 al segundo resulta una progresión aritmética, y al sumar 9 al tercero de ésta última resulta una progresión geométrica.
Sea {an} una progresión geométrica de razón r. Determina:
-
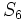 sabiendo que
sabiendo que 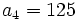 y
y 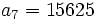
-
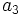 sabiendo que r=2 y
sabiendo que r=2 y 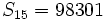
- n sabiendo que
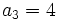 , r=2 y
, r=2 y 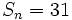
Resuelve la ecuación: 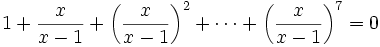
Fórmula para la obtención del capital final en un sistema de capitalización o interés compuesto como aplicación de las progresiones geométricas.
- Determina el montante obtenido al invertir 1500 € durante 5 años al 9% de interés compuesto anual.
- Determina el capital C que debe invertirse durante 4 años al 7% de interés compuesto anual para obtener un montante de 3000 €.
- Si el montante obtenido al cabo de 5 años por un capital de 1350 € es de 1702.57 €, calcula el tipo de interés compuesto anual.
- Si el interés compuesto anual es del 5%, calcula el tiempo que ha estado invertido un capital de 2100 € si el montante obtenido es de 2954.91 €
Fórmula para la obtención del capital final en un sistema de pensiones basado en un sistema de capitalización compuesta como aplicación de las progresiones geométricas.
Fórmula para la obtención de la anualidad que hay que pagar al final de cada año para amortizar un préstamo a un cierto interés.
En una progresión geométrica de razón 3, el cuarto término vale 13. Halla el término general.
En una progresión geométrica de razón 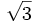 , el tercer término vale
, el tercer término vale 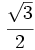 . Halla el sexto término y la suma de los seis primeros términos.
. Halla el sexto término y la suma de los seis primeros términos.
Ejercicios.
|
Problemas: Progresiones geométricas La recompensa al inventor del ajedrez: Según una leyenda india, el inventor del ajedrez solicitó, como recompensa por el invento, que se pusiera 1 grano de trigo en la primera casilla del tablero, 2 en la segunda, 4 en la tercera, y así sucesivamente; en cada una el doble que en la anterior. El rey aceptó, pero su sorpresa fue grande cuando vio, no sólo que no cabían los granos en las casillas, sino que no había suficiente trigo en todo el reino para cumplir el compromiso. Suponiendo que 10 granos de trigo pesan aproximadamente 1 g. ¿Podrías averiguar cuántos kg de trigo solicitó el inventor?Solución: a) 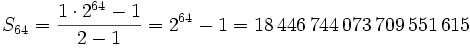 granos.
b) granos.
b) 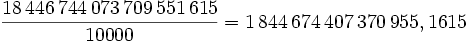 kg. kg.Una progresión increible: Supongamos que plegamos, sucesivas veces, una hoja de papel de 0.14 mm de grosor. Con cada pliegue duplicamos el grosor. Comprueba que: a) Con 22 dobleces supera la altura de la torre Eiffel (324 m). b) Con 26 dobleces supera la altura del Everest (8848 m) c) Con 50 dobleces supera la distancia de la Tierra al Sol (150 millones de km).Solución: Aquiles y la tortuga: Zenón, filósofo griego del s. V a.C., describió la siguiente paradoja: Aquiles corre a alcanzar a una tortuga que huye de él. Cuando llega donde estaba la tortuga, esta ya ha avanzado un treho. Cuando Aquiles recorre ese trecho, la tortuga avanza otro poco. Y así sucesivamente, cuando Aquiles llega a donde estaba la tortuga, esta ya ha avanzado algo. Por tanto, nunca la alcanza. Intenta demostrar que este argumento de Zenón es falso. Para ello puede suponer que Aquiles corre 10 veces más rápido que la tortuga y que inicialmente la tortuga se encuentra a una distancia de Aquiles que este tarda en recorrer, por ejemplo, 10 s. Es decir, Aquiles tardaría 10 seg en alcanzar el punto de partida de la tortuga. Una vez alcanzado este, tardaría 1 s en alcanzar la nueva posición de la tortuga, luego 1/10 s en alcanzar el siguiente, etc. Si este proceso lo repetimos infinitas veces (momento en el que se daría alcance a la tortuga), ¿cuánto tiempo habría invertido Aquiles en total?Solución: Solución: 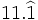 s. s. |
La leyenda del ajedrez
¿Cuántas veces se puede doblar una hoja de papel por la mitad? Te damos la solución
Paradoja de Zenon de Aquiles y la tortuga.
(Pág. 59)
Sucesiones de potencias
Una sucesión de potencias es una sucesión de la forma

De ellas, las más frecuentes son para los casos m=2 y m=3, que son las sucesiones de cuadrados y de cubos, respectivamente:
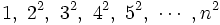
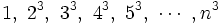
Suma de términos de las sucesiónes de cuadrados y cubos
- La suma de los n primeros términos de una sucesión de cuadrados es
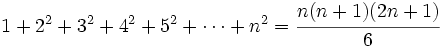
- La suma de los n primeros términos de una sucesión de cubos es
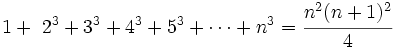
La demostración excede los niveles de este curso.
(Pág. 60)
Sucesión de Fibonacci
La sucesión de Fibonacci se debe a Leonardo de Pisa (Fibonacci), matemático italiano del siglo XIII. Es la siguiente:
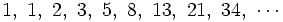
Es una sucesión recurrente dada por la siguiente relación de recurrencia:
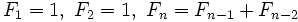
Existe también una fórmula explícita, no recurrente, para el término general:
Término general de la sucesión de Fibonacci
El término general de la sucesión de Fibonacci es:
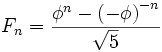
siendo 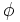 el número áureo.
el número áureo.
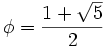
Puedes ver una demostración que sobrepasa este nivel en este enlace: enlace a wikipedia
La sucesión de Fibonacci y el número áureo
Ejemplo: La sucesión de Fibonacci y el número áureo
El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
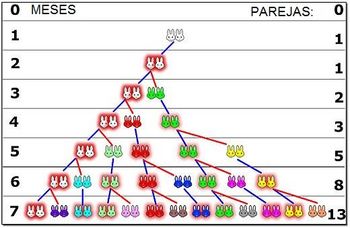
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (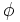 ):
):
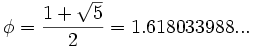
a) Sucesión de Fibonacci:
- Mes 1: 1 pareja (la pareja nace al comenzar el primer mes)
- Mes 2: 1 pareja (la pareja no es fértil hasta que termine el 2º mes)
- Mes 3: 2 parejas (al comenzar el tercer mes se reproduce por primera vez)
- Mes 4: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el comienzo del próximo mes)
- Mes 5: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 6: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 7: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene la sucesión de Fibonacci, en la que cada término se obtiene a partir de la suma de los dos anteriores:
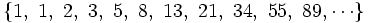
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
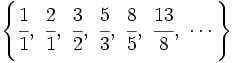
que expresada con decimales vemos que se aproxima al número áureo:
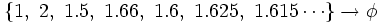
Nota: Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteamiento recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático.
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
Grandes temas de la matemática - Capítulo 4: Fibonacci. (con Adrian Paenza)
¿Tiene alguna relación la sucesión de Fibonacci y la proporción áurea? ¿Sabes qué le ha hecho más famosa?
|
Actividad: Sucesión de Fibonacci a) ¿Cuál es la sucesión de Fibonacci? b) ¿Cual es el término 10 de la sucesión de Fibonacci? c) Escribe los 15 primeros términos de la sucesión de Fibonacci d) Comprueba que la sucesión Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) Fibonacci sequence b) Fibonacci[10] c) Fibonacci[Range[1,15]] d) limit Fibonacci [n]/Fibonacci [n-1] as n->infinity |
Ejercicios
Problemas de progresiones.
Ejercicios propuestos
|
Ejercicios propuestos: Algunos tipos de sucesiones |
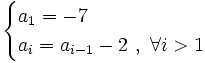
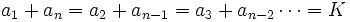
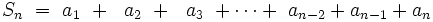
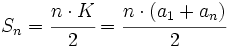
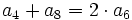
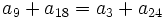
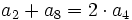
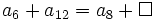
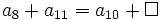
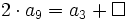
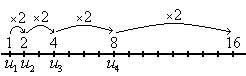
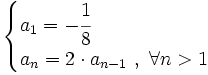


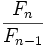 tiende al número áureo, siendo
tiende al número áureo, siendo 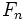 la sucesión de Fibonacci?
la sucesión de Fibonacci?

