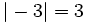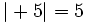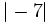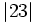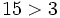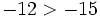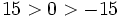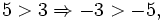El conjunto de los números enteros (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(pág. 66)
Números enteros
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
El conjunto de los números enteros
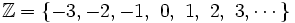
Está formado por:
- El conjunto de los números naturales o enteros positivos :
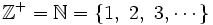 .
.
- Sus opuestos, los enteros negativos:
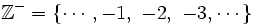 .
.
- El cero (0).
Como consecuencia, 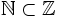 , que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
, que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
Los números enteros: utilidad y definición.
Los números enteros: utilidad y definición.
En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero.
El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación.
El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica.
Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. Los Números Naturales son todos enteros y positivos. Son muy útiles para contar, pero tienen sus limitaciones, de manera que hubo que inventar otro tipo de números...
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
(Disponibles los subtítulos en inglés)
Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica.
Los números enteros son infinitos y, al igual que los números naturales sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc.
Actividad sobre números enteros.
El termómetro y los números enteros.
Actividades sobre números enteros.
Representación de los números enteros
Representación de los números enteros
Los números enteros podemos representarlos en una recta:
- Sobre ella marcamos el número cero.
- A la derecha del cero, y a distancias iguales, se van señalando los números positivos: 1, 2, 3, ...
- A la izquierda del cero, y a distancias iguales que las anteriores, se van señalando los números negativos: −1, −2, −3, ...
- Escena en la que vas a conocer como se representan los números enteros en la recta numérica.
- Actividad en la que debes averiguar el número entero que se corresponde con un punto dado de la recta numérica.
Los números negativos en la recta numérica.
En este video vamos a ver como se representan gráficamente los números enteros sobre la recta numérica y algunos ejemplos.
Introducción a los números negativos. Representación en la recta numérica.
Representa en la recta numérica -4 y 7, e indica cuántos números enteros hay entre ellos.
|
Actividad: Números enteros. Representación
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Opuesto de un entero
El opuesto de un número entero,  , es otro número entero,
, es otro número entero, 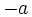 , simétrico de
, simétrico de  respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que
respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que  , pero tiene signo contrario. Lo escribiremos
, pero tiene signo contrario. Lo escribiremos 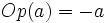 .
.
Es obvio que si 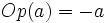 entonces
entonces 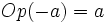 , y viceversa. Por eso, también se dice que
, y viceversa. Por eso, también se dice que  y
y 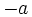 son números opuestos.
son números opuestos.
Concepto de opuesto de un número entero. Ejemplos.
Concepto de opuesto de un número entero. Ejemplos.
Opuesto de un número entero. Representación en la recta numérica.
Uso del signo "menos" para la obtención del opuesto de un número entero.
Ejercicios sobre números opuestos.
- Actividad en la que podrás ver la relación entre un número y su opuesto mediante su representación en la recta real.
- Actividad en la que deberás obtener el opuesto de un número entero.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
|
Actividad: Opuesto de un número entero
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Valor absoluto de un entero
El valor absoluto de un número entero  se representa por
se representa por 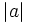 y se define de la siguiente manera:
y se define de la siguiente manera:
- Si el número es positivo, su valor absoluto es él mismo.
- Si el número es negativo, su valor absoluto es igual a su opuesto.
Propiedades
- El valor absoluto de un número es la distancia que lo separa del cero en la recta numérica.
- El valor absoluto de un número siempre es positivo o cero.
- El valor absoluto de cero es cero.
Valor absoluto de un número entero. Interpretación métrica.
- Representación de los números enteros en la recta real.
- Valor absoluto de un número entero. Interpretación métrica.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
En este video vamos a ver lo que es el valor absoluto de un número entero y también vamos a aprender a calcularlo.
Valor absoluto de un entero.
Valor absoluto como distancia entre números.
Halla 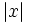 , cuando
, cuando 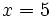 ,
, 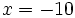 y
y 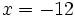 .
.
Compara:
- a)
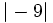 y
y 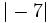
- b)
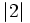 y
y 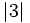
- c)
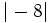 y
y 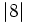
- d)
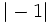 y
y 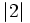 .
.
Ordena de menor a mayor: 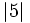 ,
, 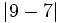 ,
, 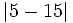 ,
, 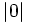 y
y 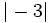 .
.
- Actividad en la que puedes obtener el valor absoluto de un número entero.
- Actividad en la que deberás obtener el valor absoluto de un número entero.
Aprende a pensar el valor absoluto como la distancia a cero, y practica encontrar valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Halla el valor absoluto.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Compara valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Cálculo de distancias mediante valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Orden en el conjunto de los enteros
En la representación de los números enteros en la recta numérica se observa el orden que existe en dicho conjunto.
Un número es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Relación de orden
Dados dos números,  y
y  , se dará uno de los siguientes casos:
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
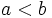 (Se lee "a es menor que b").
(Se lee "a es menor que b").
- El primero es igual que el segundo:
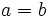 (Se lee "a es igual que b").
(Se lee "a es igual que b").
- El primero es mayor que el segundo:
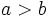 (Se lee "a es mayor que b").
(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
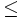 )
)
- Mayor o igual que (
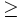 )
)
- Distinto (
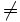 )
)
Propiedades
- Todo número negativo es menor que cero y todo número positivo es mayor que cero.
- Si dos números son positivos, el mayor es el que tiene mayor valor absoluto.
- Si dos números son negativos, el mayor es el que tiene menor valor absoluto.
- Si
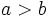 , entonces
, entonces 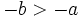
Representación y ordenación de números enteros.
Hacer una comparación de números enteros significa conocer cuál de esos números es mayor (o menor que el otro). Una forma de saberlo es haciendo la representación gráfica de esos números enteros sobre la recta. Los números situados más hacia la derecha en la recta siempre son mayores que los situados a su izquierda.
Ordenando números negativos.
Comprueba gráficamente que 5 > -5.
Comprueba gráficamente que -6 > -1.
Escribe y representa todos los números enteros más grandes que -1 y más pequeños que +5.
Escribe y representa en la recta numérica todos los números comprendidos entre -5 y 1.
Escribe y representa en la recta numérica todos los números enteros más grandes que -3 y más pequeños que 3.
Escribe un valor correcto para x e y que cumplan x < 8 < y.
Ordena de menor a mayor: 5, -3, 0, 4, -6, +1, -1, 3, -7, +6
En una estación meteorológica al sur de Argentina se realizó una medición de la temperatura en el transcurso del día, obteniendo los siguientes resultados: -10º, -3º, 12º, 1º, -8º, -5º, 4º. Ordénalos.
- Actividad en la que puedes ver como se ordenan dos números enteros comparando su posición en la recta numérica.
- Actividad para ordenar dos números enteros.
- Actividad para ordenar varios números enteros.
Ordenar números enteros.
Ordenar números enteros.
Ejercicios de autoevaluación sobre el orden en el conjunto de los números enteros.
|
Actividad: Orden en el conjunto de los números enteros
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
Repaso del tema de números enteros.
Ejercicios de autoevaluación sobre números enteros.
Actividad en la que podrás comprobar tus conocimientos sobre números enteros.
Ejercicios de autoevaluación sobre números enteros y valor absoluto.
Actividad en la que podrás comprobar tus conocimientos sobre el opuesto y el valor absoluto de un número.
Ejercicios propuestos
|
Ejercicios propuestos: El conjunto de los números enteros |

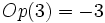 (El opuesto de 3 es -3).
(El opuesto de 3 es -3).
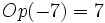 (El opuesto de -7 es 7).
(El opuesto de -7 es 7).
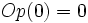 (El opuesto de 0 es 0).
(El opuesto de 0 es 0).