Radicales
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | Potencias y Raíces | WIRIS Geogebra Calculadora Raíz cuadrada |
Tabla de contenidos |
Radicales
Radical
- Un radical es cualquier expresión del tipo:
![k \cdot \sqrt[n]{a}~,~k \in \mathbb{R}](/wikipedia/images/math/c/2/6/c26445b313b501056047ed7787606a37.png)
- Si dos radicales tienen el mismo índice diremos que son homogéneos.
- Si dos radicales tienen el mismo índice y el mismo radicando diremos que son semejantes.
Radicales: homogéneos y semejantes. Ejemplos.
Radicales equivalentes
Dos o más radicales son equivalentes si se pueden poner como potencias de exponente fraccionario con la misma base y cuyos exponentes sean fracciones equivalentes.
Actividades en las que podrás aprender lo que son radicales equivalentes y cómo obtener radicales equivalentes con un índice superior (amplificación) o inferior (simplificación)
Ejercicios de autoevaluación sobre radicales equivalentes.
Reducción de radicales a índice común
La amplificación y simplificación de radicales nos va a permitir reducir radicales a índice común realizando el mínimo común múltiplo de los índice al igual que para reducir fracciones a común denominador se hacía el m.c.m. de los denominadores. No olvidemos que índice y denominador del exponente es lo mismo.
Reducción de radicales a índice común. Ejemplos.
Ejercicios de autoevaluación sobre reducción de radicales a índice común.
Ordenación de radicales
La reducción de radicales a índice común nos va a permitir ordenar cómodamente varios radicales:
Ordenación de radicales. Ejemplos.
Operaciones con radicales
Propiedades de las operaciones con radicales
Propiedades de las operaciones con radicales
1. ![\sqrt[np]{a^p}=\sqrt[n]{a}](/wikipedia/images/math/1/9/0/19055926ec943d41884a4e4efb9e3958.png)
2. ![\left ( \sqrt[n]{a}\right )^p=\sqrt[n]{a^p}](/wikipedia/images/math/0/8/f/08f48fff6b28e5860652ad48624e9b54.png)
3. ![\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}](/wikipedia/images/math/8/8/2/882098878748f7e317a403bacf091e37.png)
4. ![\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}](/wikipedia/images/math/7/3/d/73d577cd0a118df1dda404e72e4a922d.png)
5. ![\cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](/wikipedia/images/math/4/8/d/48d4191b86a6079638a33f860884bd8e.png)
Para demostrar estas propiedades basta con expresar el radical como potencia de exponente fraccionario y aplicar sus propiedades.
Ejercicios resueltos: Radicales. Propiedades
Simplificar: a) ![\sqrt[12]{x^9}](/wikipedia/images/math/9/4/2/942b2336ccb4cf42b2cbd07ed9c75ede.png) , b)
, b) ![\left ( \sqrt[3]{a^2} \right )^6](/wikipedia/images/math/9/a/1/9a1db4aea08869857d67618e54707551.png) , c)
, c) ![\sqrt{\sqrt[3]{a}}](/wikipedia/images/math/4/7/3/473cf1ea29276b3cfe84680bf3548a10.png) , d)
, d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}](/wikipedia/images/math/6/d/2/6d24beca08bdb942089cf6ad8b4c7d1c.png) , e)
, e) 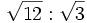
a) ![\sqrt[12]{x^9}=\sqrt[4 \cdot 3]{x^{3 \cdot 3}}=\sqrt[4]{x^{3}}](/wikipedia/images/math/d/1/9/d190b659acadff5f242846e5d6014e10.png) , usando la propiedad nº 1.
, usando la propiedad nº 1.
b) ![\left ( \sqrt[3]{a^2} \right )^6=\sqrt[3]{a^{12}}=a^{\frac{12}{3}}=a^4](/wikipedia/images/math/9/4/b/94b477fe13f98eac4d76261cf2c34d2c.png) , usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
, usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
c) ![\sqrt{\sqrt[3]{a}}=\sqrt[2 \cdot 3]{a}=\sqrt[6]{a}](/wikipedia/images/math/9/4/a/94ad123ac81d4cf1d017be5a726de942.png) , usando la propiedad nº 3.
, usando la propiedad nº 3.
d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}= \sqrt[3]{3 \cdot 9} =\sqrt[3]{27}=3](/wikipedia/images/math/b/7/b/b7b21e3525e1caa80c30fe91bbb85c77.png) , usando la propiedad nº 4.
, usando la propiedad nº 4.
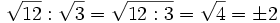 , usando la propiedad nº 5.
, usando la propiedad nº 5.Actividades en las que podrás aprender las propiedades de las operaciones con radicales del mismo índice.
Tutorial que explica las propiedades básicas de los radicales, con ejemplos resueltos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Ejemplos sencillos de aplicación de las propiedades de las operaciones con radicales.
Simplifica: 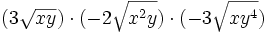
Simplifica: ![(-8\sqrt[3] {x^{10}y^2}) : (-4\sqrt[3] {xy^{11}})](/wikipedia/images/math/2/1/b/21b675f2e891ca1cd137acdf888cbcde.png)
Calcula: ![\sqrt[4]{\cfrac{81}{16}}](/wikipedia/images/math/9/e/d/9ed2bdc3b33dce510e788cce2d6938b7.png)
Calcula:
1) 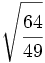 2)
2) ![\sqrt[4]{\cfrac{1}{81}}](/wikipedia/images/math/a/5/4/a54618bf9ee77a830fab9a825f43fad0.png) 3)
3) ![\sqrt[3]{\cfrac{-27~~}{125}}](/wikipedia/images/math/5/c/3/5c3b48c07709122b11aadf157c159924.png) 4)
4) ![\sqrt[5]{\cfrac{-32~~}{243}}](/wikipedia/images/math/7/5/8/758e101bb00fde536dd8dc589f2eab1d.png)
Suma y resta de radicales semejantes
Para sumar y restar radicales, éstos deben ser semejantes, es decir, tener el mismo radicando y el mismo índice. En tal caso el radical el radical resultante tiene como coeficiente la suma o resta de los coeficientes de cada uno de los radicales.
Ejemplo: Suma y resta de radicales semejantes
Efectúa las siguientes sumas y restas de radicales:
1. 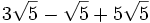
2. 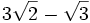
3. ![3\sqrt[3]{2}+\sqrt{2}](/wikipedia/images/math/f/5/5/f554a76b3698de9bd3d86d6600364c25.png)
1. 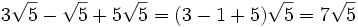
2. 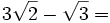 (No se puede simplificar)
(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png) (No se puede simplificar)
(No se puede simplificar)Actividades
En los siguientes videotutoriales vamos a repasar las operaciones con radicales vistas hasta ahora, antes de pasar a ver otros casos de mayor dificultad.
- Definición de radical y de radicales semejantes.
- Suma de radicales semejantes.
- Radicales opuestos.
- Resta de radicales semejantes.
- Producto de radicales del mismo índice.
- División de radicales del mismo índice.
- Potencia de un radical.
- Raíz de un radical.
1) Radicales semejantes:
- 1a) Escribe tres radicales semejantes y tres que no lo sean.
- 1b) Escribe dos radicales semejantes opuestos.
2) Calcula:
- 2a)
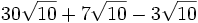
- 2b)
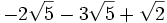
- 2c)
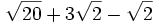
- 2d)
![-3 \sqrt[3]{11}+\sqrt[3]{11}-8 \sqrt[3]{11}\;](/wikipedia/images/math/3/8/6/386dda78a1c0a8e06a7d92ad446cca8a.png)
- 2e)
![-8 \sqrt[3]{11}+4 \sqrt[3]{11}-2 \sqrt[3]{11}\;](/wikipedia/images/math/9/b/c/9bc9cc4fe2abf85a102fd7edd8a91a3e.png)
- 2f)
![\sqrt[3]{-5}-5 \sqrt[3]{-5}+2 \sqrt[3]{-5}\;](/wikipedia/images/math/7/9/7/797db9d9f2a327215cf66dc0fd1a0989.png)
- 2g)
![6 \sqrt[8]{3}+12 \sqrt[8]{3}-4 \sqrt[8]{3}\;](/wikipedia/images/math/e/a/3/ea3c1128b9341e9ee92e9adf7dbf36e8.png)
- 2h)
![5 \sqrt[11]{-8}+9 \sqrt[11]{-8}- \sqrt[11]{-8}\;](/wikipedia/images/math/c/f/c/cfc360decb13c219ecfed5246e616bbc.png)
- 2i)
![-\sqrt[5]{3}- \sqrt[5]{3}-4 \sqrt[5]{3}\;](/wikipedia/images/math/c/d/0/cd013a1ff11c225a935a2891232efb7a.png)
3) Halla el opuesto de los siguiente radicales y después suma cada radical con su opuesto:
- 3a)
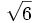
- 3b)

- 3c)
![-5\sqrt[3]{2}\;](/wikipedia/images/math/2/9/b/29ba151ca92717a7ec2fce60d9a43887.png)
- 3d)
![-8\sqrt[3]{-3}\;](/wikipedia/images/math/4/4/a/44af796a04099974506078fbdaa97c8e.png)
- 3e)
![14\sqrt[3]{5}\;](/wikipedia/images/math/a/8/b/a8b18bd1e94168e14bdfa178486c55de.png)
- 3f)
![-5\sqrt[4]{7}\;](/wikipedia/images/math/9/c/3/9c3b71fe66e4cd559e4c1c3e2d8f0d50.png)
4) Calcula:
- 4a)
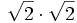
- 4b)
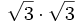
- 4c)
![\sqrt[3]{2} \cdot \sqrt[3]{2} \cdot \sqrt[3]{2} \;](/wikipedia/images/math/8/b/7/8b72eb2e695638b1b598aa91906d2afd.png)
- 4d)
![\sqrt[3]{5} \cdot \sqrt[3]{5} \cdot \sqrt[3]{5} \;](/wikipedia/images/math/4/7/0/4706a180f7cecca86f552cb03bc61723.png)
- 4e)
![\sqrt[4]{3} \cdot \sqrt[4]{3} \cdot \sqrt[4]{3} \cdot \sqrt[4]{3} \;](/wikipedia/images/math/8/7/1/871aec8b9c551d588f6bb0f7652776b0.png)
- 4f)
![\sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \;](/wikipedia/images/math/c/6/1/c61ef44eacb7a1efa0af29b13e778c84.png)
- 4g)
![\sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2}\;](/wikipedia/images/math/b/a/a/baaf1e13d7ae13183caee280ed997078.png)
- 4h)
![\sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \;](/wikipedia/images/math/3/0/4/3044aa9fbabf7c1d05d005d3d067c642.png)
- 4i)
![\sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \;](/wikipedia/images/math/f/2/4/f24f9a63eafe40b3e6d366a5e52f6be1.png)
- 4j)
![\sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2}\;](/wikipedia/images/math/5/6/9/5699ece51e33ce84d469d13405c1a662.png)
5) Calcula:
- 5a)
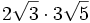
- 5b)
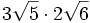
- 5c)
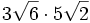
- 5d)
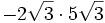
- 5e)
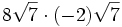
- 5f)
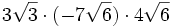
- 5g)
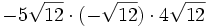
- 5h)
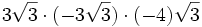
- 5h)
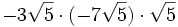
5) Calcula:
- 5i)
![2\sqrt[3]{3} \cdot 3\sqrt[3]{3} \;](/wikipedia/images/math/e/b/8/eb885ee9f22a7b60f1fba48b165a9bba.png) ; 5j)
; 5j) ![3\sqrt[3]{5} \cdot 2\sqrt[3]{5} \;](/wikipedia/images/math/7/4/8/74817e09bd26600d541bc7f27acc2721.png) ; 5k)
; 5k) ![3\sqrt[3]{6} \cdot 5\sqrt[3]{6} \;](/wikipedia/images/math/4/d/7/4d731dfeb72737e5ea4b3fae68d986bc.png)
- 5l)
![-2\sqrt[3]{3} \cdot 5\sqrt[3]{3} \;](/wikipedia/images/math/b/d/0/bd0bdd2316e3647e561f42eea5e49432.png) ; 5m)
; 5m) ![8\sqrt[3]{-7} \cdot \sqrt[3]{-2} \cdot \sqrt[3]{-7} \;](/wikipedia/images/math/d/e/6/de6d9da92635aa3ed672a1d37bbb9d1e.png) ; 5n)
; 5n) ![3\sqrt[3]{3} \cdot (-7\sqrt[3]{3}) \cdot 4\sqrt[3]{3} \;](/wikipedia/images/math/8/d/7/8d7ab02625222fb400fbef68aae4f1a9.png)
- 5o)
![-5\sqrt[3]{12} \cdot (-\sqrt[3]{12}) \cdot 4\sqrt[3]{12} \;](/wikipedia/images/math/2/4/d/24db05991b4866bee0cf063c06a2a5a4.png) ; 5p)
; 5p) ![3\sqrt[3]{3} \cdot (-3\sqrt[3]{3}) \cdot (-4\sqrt[3]{3}) \;](/wikipedia/images/math/0/b/1/0b12fb80b6b5d9ab9cff8bdda29e3670.png) ; 5q)
; 5q) ![-3\sqrt[3]{5} \cdot (-7\sqrt[3]{5}) \cdot \sqrt[3]{5} \;](/wikipedia/images/math/4/9/3/493e61292a0c10080a211793ad3d938a.png)
6) Calcula:
- 6a)
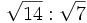 ; 6b)
; 6b) 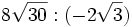 ; 6c)
; 6c) 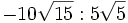
- 6d)
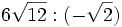 ; 6e)
; 6e) 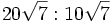 ; 6f)
; 6f) ![\sqrt[3]{14} : \sqrt[3]{7} \;](/wikipedia/images/math/e/5/5/e55782cffbcf990bcc3401f1a26c47b6.png)
- 6g)
![9\sqrt[3]{14} : (-\sqrt[3]{-7}) \;](/wikipedia/images/math/e/a/6/ea6ac7a2061e05e92f94b80d4af19663.png) ; 6h)
; 6h) ![-10\sqrt[3]{15} : 5\sqrt[3]{5} \;](/wikipedia/images/math/c/3/0/c308580a14622890c46723f7fdf783fb.png) ; 6i)
; 6i) ![12\sqrt[3]{18} : (-6\sqrt[3]{-9}) \;](/wikipedia/images/math/0/5/9/05982cd16e41d3ae4cdc9d011905ad4b.png)
- 6j)
![-30\sqrt[3]{14} : 6\sqrt[3]{7} \;](/wikipedia/images/math/0/0/9/00930632b62d29b0446beb2eb4585c39.png) ; 6k)
; 6k) ![\sqrt[4]{14} : \sqrt[4]{7} \;](/wikipedia/images/math/3/7/d/37d6db29364ddf586bf938556c44bf69.png) ; 6l)
; 6l) ![9\sqrt[4]{14} : (-\sqrt[4]{7}) \;](/wikipedia/images/math/c/1/2/c12d93323a255c0807c702a7d1c4fd3a.png)
- 6m)
![-10\sqrt[4]{15} : 5\sqrt[4]{5} \;](/wikipedia/images/math/f/b/4/fb47b8279375acea84ad3b6776fe52d9.png) ; 6n)
; 6n) ![12\sqrt[4]{18} : (-6\sqrt[4]{9}) \;](/wikipedia/images/math/0/e/e/0ee9a8d792aa42be622074880b8c1737.png) ; 6o)
; 6o) ![-30\sqrt[4]{14} : 6\sqrt[4]{7}) \;](/wikipedia/images/math/f/8/6/f86747fe7edf79f2f565ae3b47c5f5cc.png)
- 6p)
![\sqrt[5]{14} : \sqrt[5]{7} \;](/wikipedia/images/math/c/e/d/cedeedebf22023c7095857fdb5f89cd9.png) ; 6q)
; 6q) ![9\sqrt[5]{14} : (-\sqrt[5]{7}) \;](/wikipedia/images/math/a/0/8/a0809badb27cd335d6d595e07efabe29.png) ; 6r)
; 6r) ![-10\sqrt[5]{15} : 5\sqrt[5]{5}) \;](/wikipedia/images/math/b/9/9/b99dbf9eb1bd9e64b5651116476d3105.png)
7) Calcula:
- a)
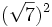 ; b)
; b) ![(\sqrt[3]{7})^3\;](/wikipedia/images/math/e/3/6/e3645d99093cd9065fb2082d8c6c6c01.png) ; c)
; c) ![(\sqrt[4]{7})^4\;](/wikipedia/images/math/8/4/f/84f808c115fe3de548ae9bfe5824709f.png) ; d)
; d) 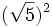 ; e)
; e) ![(\sqrt[3]{5})^3\;](/wikipedia/images/math/f/2/b/f2bf6748d06d16bcaae81f483dfd71c9.png)
- f)
![(\sqrt[4]{21})^4\;](/wikipedia/images/math/d/e/7/de71424f30904a433e21926aea5c19ea.png) ; g)
; g) 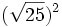 ; h)
; h) ![(\sqrt[3]{-25})^3\;](/wikipedia/images/math/4/7/8/478cc6706fac0d47cfc87e4c40c1a9fa.png) ; i)
; i) ![(\sqrt[4]{100})^4\;](/wikipedia/images/math/6/1/d/61d8bd6207295d4b3de801045656acdb.png) ; j)
; j) 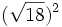
- k)
![(\sqrt[3]{-100})^3\;](/wikipedia/images/math/e/1/6/e16420641a6f36c33546ff527203864c.png) ; l)
; l) ![(\sqrt[5]{16})^5\;](/wikipedia/images/math/8/0/2/802fdd52c9cc6b2275f4ecb0a8ca4ae1.png) ; m)
; m) 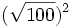 ; n)
; n) ![(\sqrt[3]{18})^3\;](/wikipedia/images/math/b/c/c/bcc549d18d80fd5c5888a59db21937bf.png) ; o)
; o) ![(\sqrt[6]{12})^6\;](/wikipedia/images/math/5/9/7/597c0afad70f17b1f3788787dfd0974a.png)
8) Calcula:
- a)
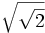 ; b)
; b) 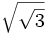 ; c)
; c) 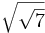 ; d)
; d) ![\sqrt[3]{\sqrt{2}}\;](/wikipedia/images/math/5/7/5/5750c75c078868e9954cfd490001321d.png)
- e)
![\sqrt[3]{\sqrt[3]{25}}\;](/wikipedia/images/math/a/6/1/a61140b4f250a3cb23f5d4156fc505bd.png) ; f)
; f) ![\sqrt{\sqrt[3]{64}}\;](/wikipedia/images/math/e/2/3/e23312ed4b7fe23d8f48d5afad9e73be.png) ; g)
; g) ![\sqrt[4]{\sqrt[3]{2}}\;](/wikipedia/images/math/1/7/7/17747fd8e1ef3646625fd5f03e380c01.png) ; h)
; h) ![\sqrt[3]{\sqrt{128}}\;](/wikipedia/images/math/1/7/e/17e0360d6aab8d041cd7f8c090dbc6c1.png)
Radicales (Ampliación)
Extracción e introducción de factores en un radical
El siguiente videotutorial resume lo que se va a a ver en este apartado:
Tutorial que explica cómo extraer factores de un radical, que se utiliza principalmente para simplificar radicales, y de cómo introducir factores dentro.
Extracción de factores
Procedimiento
Para extraer factores de un radical se divide el exponente (m) del factor entre el índice (n) del radical. A continuación, se saca el factor elevado al cociente (c) de la división, quedando dentro del radical el factor elevado al resto (r).
![\sqrt[n]{a^m}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/5/e/c/5ecb8e4f6515ae774c6eef7fea5c576e.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Fíjate que en (1) hemos usado la regla de la divsión:
Para extraer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Ejemplo: Extracción de factores de un radical
Extrae todo lo que se pueda de este radical: ![\sqrt[3]{6000}](/wikipedia/images/math/5/c/2/5c28fba2f76ed7b33ea1b13e448c224f.png)
![\sqrt[3]{6000}=\sqrt[3]{2^4 \cdot 3 \cdot 5^3}=2 \cdot 5 \sqrt[3]{2 \cdot 3}=10\sqrt[3]{6}](/wikipedia/images/math/6/9/f/69fad43d23404b125d2e89b1f9479c74.png)
Extracción de factores de un radical. Ejemplos.
Extracción de factores de un radical utilizando un símil curioso.
Extracción de factores de un radical. Ejemplos
Extracción de factores de un radical.
Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: Simplifica: Simplifica: | Simplifica: Extrae todos los factores posibles del radicando:
Extrae todos los factores posibles del radicando:
Simplifica: Simplifica: Simplifica:
Simplifica: Simplifica: Simplifica: |
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Extrae factores fuera del radical.
Extrae factores fuera del radical.
Extrae factores fuera del radical (con variables).
Extrae factores fuera del radical (con variables).
Introducción de factores
Procedimiento
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical.
![a \sqrt[n]{b}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/8/5/f/85f82704cfc0f9e1418d853a9e18061d.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Ejemplo: Introducción de factores en un radical
Introduce los factores dentro del radical: ![10 \sqrt[3]{6}](/wikipedia/images/math/b/0/5/b059e301f3cf30968be2c858922be777.png)
![10 \sqrt[3]{6}=\sqrt[3]{6 \cdot 10^3}=\sqrt[3]{6000}](/wikipedia/images/math/f/c/a/fca24b7a66a69b8d0a52ef1d1f43ef96.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introduce dentro del radical: 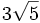
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![a^3 b^2 \sqrt[4]{c}](/wikipedia/images/math/0/f/2/0f257d67a28e35c2fe66d6e47ec6170b.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![m^2 n^5 \sqrt[5]{m^3 p^2}](/wikipedia/images/math/2/7/6/276aa6fd087cafe6e44377e54dfae158.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando. Si dentro del radical tenemos otra potencia con la misma base entonces sumaremos el exponente de la potencia que entra con el de dentro del radical.
Introduce factores dentro del radical:
- a)
![4 \sqrt[3]{6}](/wikipedia/images/math/0/9/8/09832a2fdbea98af094bc3b99a2f71fb.png)
- b)
![2^4 \cdot 3^2 \sqrt[6]{2^2 \cdot 3^5}](/wikipedia/images/math/a/3/e/a3e7fc4c36dc72ff46d3e14c87570f8c.png)
- b)
![a^7 \cdot b^8 \sqrt[5]{b^2}](/wikipedia/images/math/7/1/c/71c6e44e4a1a1f816fefc0e45b931acc.png)
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre introducción y extracción de factores de un radical.
Suma y resta de radicales con el mismo índice y distinto radicando
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.
Ejemplo: Suma y resta de radicales con el mismo índice y distinto radicando
Resta los siguientes radicales: 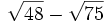
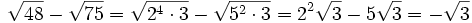
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Tutorial que explica cómo sumar y restar radicales. La suma y resta son operaciones que "se llevan muy mal" con el resto de operaciones y hay que tener mucho cuidado a la hora de hacerlo con radicales.
Suma y resta de radicales con el mismo índice. Ejemplos.
Simplifica: 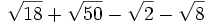
Simplifica: 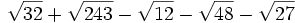
Calcula:
- a)
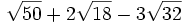
- b)
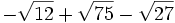
- c)
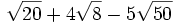
- d)
![\sqrt[3]{48}+\sqrt[3]{1080}-\sqrt[3]{96}\;](/wikipedia/images/math/2/d/6/2d67b353649768215c317a719b4f248d.png)
- e)
![-\sqrt[3]{-27}+2\sqrt[3]{272}-9\sqrt[3]{-81}\;](/wikipedia/images/math/c/0/f/c0ff906569b1db6871629962fc420418.png)
Calcula:
- a)
![\sqrt[4]{32}+8\sqrt[4]{16}-\sqrt[4]{80}\;](/wikipedia/images/math/4/c/a/4cac9ae91631e9811be06e223293e340.png)
- b)
![\sqrt[5]{64}-6\sqrt[5]{32}+5\sqrt[5]{96}\;](/wikipedia/images/math/7/a/f/7af16a27ecbd28162b9ffd8bcc06a665.png)
- c)
![-9\sqrt[6]{64}+\sqrt[6]{192}-\sqrt[6]{960}\;](/wikipedia/images/math/4/5/c/45c6fc0df3cf3b4245b56dcf055735ec.png)
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Producto y cocientes de radicales con distinto índice
Para multiplicar o dividir radicales con distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.
Ejemplo: Producto y cocientes de radicales con distinto índice
Reduce a un solo radical ![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}](/wikipedia/images/math/5/9/7/597ebbc8a8a1e63faeabbecf3da740ef.png)
Para reducir los radicales a índice común calculamos el m.c.m de los índices: m.c.m.(3,4,2)=12 y elevamos cada radicando al resultado de dividir el m.c.m. por el índice de cada radical.
![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}=\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}](/wikipedia/images/math/e/8/1/e81ffde8d1c752d66e97b66e25149a0f.png)
Luego multiplicamos o dividimos los radicandos, ya que ahora los índices son iguales:
![\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}=\sqrt[12]{10^4 \cdot 5^3 : 8^6}](/wikipedia/images/math/6/d/1/6d1f82fd6b85971e0e493c1e7eb2d485.png)
Finalmente simplificamos:
![\sqrt[12]{10^4 \cdot 5^3 : 8^6}=\sqrt[12]{2^4 \cdot 5^4 \cdot 5^3 : (2^3)^6}=\sqrt[12]{2^{-14} \cdot 5^7}](/wikipedia/images/math/7/0/e/70e1e7afd0d65ac459a2b76336b7fbb6.png)
Producto y cociente de radicales con el mismo o con distinto índice. Ejemplos.
Simplifica: ![(8\sqrt[3]{a^2b}) \cdot (4\sqrt{ab^3})](/wikipedia/images/math/8/e/a/8ea372bbacf499b888b5f31aeb1cae8b.png)
Simplifica: ![\sqrt[3]{27^{-2}} : \sqrt[4]{16}](/wikipedia/images/math/1/0/d/10dcb2912a1fddcdb4f0013df23cedc3.png)
Actividades en las que podrás aprender a multiplicar y dividir radicales de distinto índice previa reducción a índice común.
Ejercicios de autoevaluación sobre productos de radicales.
Ejercicios de autoevaluación sobre cocientes de radicales.
Potencias de radicales
Potencias de radicales. Ejemplos.
Ejercicios de autoevaluación sobre potencias de radicales.
Radicales dobles (Avanzado)
Convierte los siguientes radicales dobles en sencillos:
a) 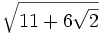
b) 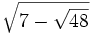
Convierte los siguientes radicales dobles en sencillos:
a) 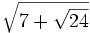
b) 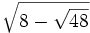
Convierte los siguientes radicales sencillos en dobles:
a) 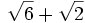
b) 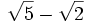
Actividades
Simplifica:
a)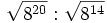
b)![\sqrt[6]{\sqrt{8}}](/wikipedia/images/math/b/d/b/bdbeee310b4a724e942f08bffbfa8d23.png)
c)![\sqrt[9]{12} \cdot \sqrt{3}](/wikipedia/images/math/7/2/8/72833303cca23937986fcffc7c483ab7.png)
Simplifica: 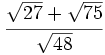
Simplifica: ![\sqrt [4]{\sqrt{x^3} \cdot 16 \sqrt{x}}](/wikipedia/images/math/c/b/1/cb16004d071779fc6b1ffc6f93945a68.png)
Simplifica: ![\left(\cfrac{\sqrt [6]{32}}{\sqrt{8}} \right)^3](/wikipedia/images/math/e/a/c/eacfafeb055cc8c9cdb0aad1d2009d5a.png)
Simplifica (Extracción e introducción de factores en un radical):
a) ![\sqrt[3]{5^{17} \cdot 4^6}](/wikipedia/images/math/0/0/5/005d7f0a77ef68096dbc57b6faf62174.png)
b) ![\sqrt[3]{16\, a^4\, b^{21}}](/wikipedia/images/math/1/0/a/10a9ce8e21e1692804f04887051c25a2.png)
c) ![7^3 \cdot 6^9 \sqrt[11]{y^3}](/wikipedia/images/math/6/d/d/6dd037766dcba2853e802af0eb172662.png)
Simplifica:
a) 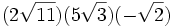
b) ![(5\sqrt[3]{4})(2\sqrt[3]{2})](/wikipedia/images/math/c/4/a/c4a86a9d45d3ab1a13edab27c030aed9.png)
c) ![(7\sqrt{2})(5\sqrt[3]{3})](/wikipedia/images/math/9/8/1/981355fbebaebcc7ed55c7fad7b969d5.png)
Simplifica:
a) 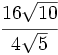
b) ![\cfrac{24\sqrt[4]{2}}{4\sqrt[5]{3}}](/wikipedia/images/math/b/3/c/b3c493d2101ba7fdd69acb88e870ea21.png)
Simplifica:
a) 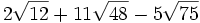
b) 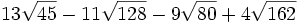
Simplifica:
a) ![3\sqrt[5]{2}+7\sqrt[5]{2}](/wikipedia/images/math/d/2/7/d27d96074bab9896a713780d59467405.png)
b) 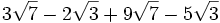
c) ![3\sqrt[3]{54}-2\sqrt[3]{2}+9\sqrt[3]{16}](/wikipedia/images/math/1/d/0/1d09e34f1f3456a7a3bee748760e4d4f.png)
d) ![4\sqrt[4]{25}-\sqrt{45}](/wikipedia/images/math/d/d/b/ddb97312176c5bcecf2ee242e8ad1131.png)
e) ![\cfrac{1}{2}\sqrt[3]{108}-\cfrac{3}{2}\sqrt[3]{4}](/wikipedia/images/math/b/d/5/bd562c177c7713390d93927f9b4bc7d4.png)
Calcula y simplifica:
- a)
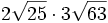 ; b)
; b) 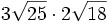 ; c)
; c) 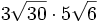
- d)
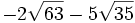 ; e)
; e) 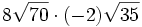 ; f)
; f) 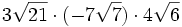
- g)
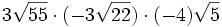 ; f)
; f) 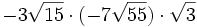
Opera y simplifica:
- a)
![2\sqrt[3]{18} \cdot 3\sqrt[3]{12}\;](/wikipedia/images/math/0/3/1/031733f0fbd54f968faa9fe5eda8d0a5.png) ; b)
; b) ![3\sqrt[3]{50} \cdot 2\sqrt[3]{20}\;](/wikipedia/images/math/5/3/2/5325b2d9d555d9f858cb45e672a5d4f1.png) ; c)
; c) ![3\sqrt[3]{45} \cdot 5\sqrt[3]{75}\;](/wikipedia/images/math/d/0/3/d03eb8f8d36666972cc949f4aa84135f.png)
- d)
![-2\sqrt[3]{28} \cdot 5\sqrt[3]{98}\;](/wikipedia/images/math/a/e/0/ae069089d23479aab015b6e60f86d52f.png) ; e)
; e) ![8\sqrt[3]{-12} \cdot (-3\sqrt[3]{3}) \cdot \sqrt[3]{-6}\;](/wikipedia/images/math/4/c/2/4c2775ca1af101fe6d39c7594ff03cf3.png) ; f)
; f) ![3\sqrt[3]{8} \cdot (-7\sqrt[3]{9}) \cdot 4\sqrt[3]{3}\;](/wikipedia/images/math/7/6/2/762033e0f8daa6c889ef1b8ff3aedd7a.png)
- g)
![-5\sqrt[3]{27} \cdot (-\sqrt[3]{4}) \cdot 4\sqrt[3]{2}\;](/wikipedia/images/math/c/7/a/c7a78297a356e0f2492f0896287bf16f.png) ; h)
; h) ![3\sqrt[3]{20} \cdot (-3\sqrt[3]{10}) \cdot (-4\sqrt[3]{5})\;](/wikipedia/images/math/6/6/6/666f233d469263babf8b6568f8816f5f.png) ; i)
; i) ![3\sqrt[6]{324} \cdot 5\sqrt[6]{144}\;](/wikipedia/images/math/d/3/e/d3ec755367d0b6a0b64cb68db1a7cd6d.png)
- j)
![-2\sqrt[4]{250} \cdot 5\sqrt[4]{40}\;](/wikipedia/images/math/4/5/9/45941ba5c1a9b2af7e5f5acfe1ab8614.png) ; k)
; k) ![3\sqrt[4]{88} \cdot (-7\sqrt[8]{216}) \cdot 4\sqrt[8]{162}\;](/wikipedia/images/math/4/8/6/48604a9cfa646b3261cb09804c4afc34.png)
Opera y simplifica:
- a)
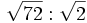 ; b)
; b) 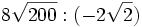
Opera y simplifica:
- a)
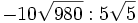 ; b)
; b) 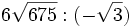 c)
c) 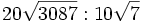
- d)
![9\sqrt[3]{432} : (-\sqrt[3]{-2})\;](/wikipedia/images/math/f/b/9/fb95dd8cbe8cfd4e0c49eec43dda6ff7.png) ; e)
; e) ![-10\sqrt[3]{1458} : 5\sqrt[3]{2}\;](/wikipedia/images/math/e/e/f/eef5a8ba7329df0a841ecd829db26562.png) ; f)
; f) ![12\sqrt[3]{192} : (-6\sqrt[3]{-3})\;](/wikipedia/images/math/8/0/7/807881bc4d10def8325191dac48379b0.png)
- g)
![-30\sqrt[3]{3000} : 6\sqrt[3]{3}\;](/wikipedia/images/math/f/f/e/ffec5e6b75ac1f80c24af9caa431a158.png) ; h)
; h) ![\sqrt[4]{512} : \sqrt[4]{2}\;](/wikipedia/images/math/0/b/5/0b5ce95019fc14a1775557e6ba43ac1b.png) ; i)
; i) ![9\sqrt[4]{768} : (-\sqrt[4]{3})\;](/wikipedia/images/math/0/6/5/06566e947dc6e1be1bb70ce72612c1b0.png)
- j)
![-10\sqrt[4]{2592} : 5\sqrt[4]{2}\;](/wikipedia/images/math/5/9/c/59c73064c6c6c8edd9a75643e619e889.png) ; k)
; k) ![12\sqrt[4]{3888} : (-6\sqrt[4]{3})\;](/wikipedia/images/math/e/6/f/e6f826708d9b60ae3eec0ce03419beaa.png) ; l)
; l) ![-30\sqrt[4]{13122} : 6\sqrt[4]{2}\;](/wikipedia/images/math/f/3/8/f38325af6ab9a4b792be123712a935eb.png)
Calcula:
- a)
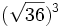 ; b)
; b) 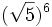 ; c)
; c) 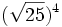 ; d)
; d) 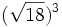
Calcula:
- a)
![(\sqrt[3]{-100})^4\;](/wikipedia/images/math/f/9/8/f9898c4fea7d81c6a960d595902aed45.png) ; b)
; b) ![(\sqrt[3]{18})^4\;](/wikipedia/images/math/b/8/2/b821a9571353a23729e0d70db373b576.png) ; c)
; c) ![(\sqrt[4]{7})^5\;](/wikipedia/images/math/7/e/5/7e5c3062446a9e6e968bcc8e047c05f2.png) ; d)
; d) ![(\sqrt[4]{21})^7\;](/wikipedia/images/math/d/2/2/d2219bd465cdf2cd6bd4ee043a87fa68.png)
- e)
![(\sqrt[4]{100})^5\;](/wikipedia/images/math/d/e/e/dee501759eec044d5e4b65b67661a26a.png) ; f)
; f) ![(\sqrt[5]{16})^7\;](/wikipedia/images/math/c/4/7/c477f227f0e345150bd5d4465006a35c.png) ; g)
; g) ![(\sqrt[6]{12})^7\;](/wikipedia/images/math/a/f/f/aff12187841d83e96f42fc74b7813d9e.png)
Calcula y simplifica:
- a)
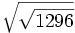 ; b)
; b) 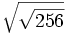 ; c)
; c) ![\sqrt[3]{\sqrt{46\,656}}\;](/wikipedia/images/math/4/4/b/44b6d41e62a3bb8b4f098b0be493b394.png)
- d)
![\sqrt[3]{\sqrt[3]{4096}}\;](/wikipedia/images/math/b/a/5/ba5c5b911a2c67423eff1042451512d8.png) ; e)
; e) ![\sqrt{\sqrt[3]{1024}}\;](/wikipedia/images/math/0/d/f/0df78f26900c5ba4320ea30e1acdadc1.png) ; f)
; f) ![\sqrt[4]{\sqrt[3]{4096}}\;](/wikipedia/images/math/4/3/8/4388e0aec792ebc9974cea4ab170a49d.png)
En esta escena podrás practicar la suma y resta de radicales con o sin el mismo índice.
Ejercicios de autoevaluación sobre sumas y restas de radicales.
Ejercicios de autoevaluación sobre raíces de radicales.
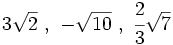
![3\sqrt[3]{2} \ , \ -\sqrt[3]{2} \ , \ \cfrac{2}{3}\sqrt[3]{2}](/wikipedia/images/math/1/1/c/11ca38664b260e771d7b6b60dd01d52b.png)
![\sqrt[n]{a^m}= a^{\frac{m}{n}} \begin{matrix} ~_{(1)}~ \\ = \\ \, \end{matrix} a^{c+\frac{r}{n}}= a^c \cdot a^{\frac{r}{n}}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/d/3/9/d39083130ff7fc81f2df907b77c139e4.png)
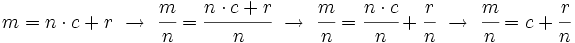
 b)
b) 
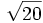 b)
b) 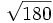
![\sqrt[3]{16}\;](/wikipedia/images/math/5/3/a/53a3c4a84f10981709eb9cbe55fd96d6.png) b)
b) ![\sqrt[3]{72}\;](/wikipedia/images/math/7/3/2/73202ad33b01491941443d47216fb27f.png)
![\sqrt[5]{96}\;](/wikipedia/images/math/9/d/c/9dcae009beea43dfbe3404b5f004cc4a.png) b)
b) ![\sqrt[4]{405}\;](/wikipedia/images/math/a/8/9/a890f47fe2c93a2f06c95c8202cb8251.png)
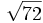 b)
b) ![\sqrt[4]{3645}\;](/wikipedia/images/math/6/4/e/64e81b0470d1d706dc6259ee3c15b821.png) c)
c) 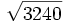 c)
c) ![5\,\sqrt[3]{384}\;](/wikipedia/images/math/4/9/0/4905ec017f8b5e0d98f7ee1f7eec1207.png)
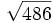 b)
b) ![6\sqrt[3]{1250}\;](/wikipedia/images/math/4/3/4/4346e96a7c5105fca5f88837843083a9.png) c)
c) ![m^3n\sqrt[5]{m^{20}n^{37}}\;](/wikipedia/images/math/4/9/6/496807e951625205ca38c068a23ebc66.png)
![-2\sqrt [3]{16x^5yz^9}](/wikipedia/images/math/5/d/a/5da6c4122805a4279103f0cf5cfb13c0.png)
![\sqrt [4]{32x^4y^{21}z^{43}}](/wikipedia/images/math/c/4/f/c4f4294a30ee9a53a181d8f3abd8d54b.png)
![\sqrt [5]{32x^5y^{-10}z^{-35}}](/wikipedia/images/math/e/f/b/efb9fab775fddc918c97f70c90e23eb4.png)
![\sqrt [5]{-243a^{20}}](/wikipedia/images/math/e/e/3/ee38623c8fe3fac34be9faf93f9e8457.png)
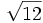 ; b)
; b) 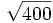 ;
;
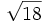 ; e)
; e) 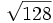
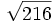 ; g)
; g) 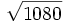 ; h)
; h) ![\sqrt[3]{625}\;](/wikipedia/images/math/e/5/d/e5d68b00dfbd79e2f3d58e0aca3d7c0f.png)
![\sqrt[3]{432}\;](/wikipedia/images/math/6/d/1/6d13f38f4d1eb2019980f043401b4212.png) ; j)
; j) ![\sqrt[3]{-216}\;](/wikipedia/images/math/f/2/e/f2e9196b5535a696cacaea492b5fca1f.png) ; k)
; k) ![\sqrt[3]{243}\;](/wikipedia/images/math/8/f/5/8f5ffd08c6adee125672bdaceac21095.png)
![\sqrt[4]{1296}\;](/wikipedia/images/math/d/f/8/df8a4653fd51d5f3a467722317d864f7.png) ; m)
; m) ![\sqrt[4]{20736}\;](/wikipedia/images/math/e/0/3/e0364ebd0e97bb3e82e855e75e9794bd.png) ; n)
; n) ![\sqrt[5]{-480}\;](/wikipedia/images/math/f/5/e/f5e99ceeb09f023ea88f8aae9d707acc.png)
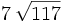
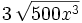
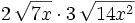
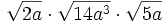
![5\,\sqrt[3]{2x^2} \cdot 3\,\sqrt[3]{4x^4}\;](/wikipedia/images/math/b/4/5/b4564f0c1cace422e46c7b4e8bef605e.png)
![\sqrt[3]{125x^6y^3}](/wikipedia/images/math/6/4/b/64b184793ed736d13012a61c0bb6a166.png)
![\sqrt[4]{5a^4b^{12}}](/wikipedia/images/math/a/b/a/abab543450564364e8ced43319182eb4.png)
![a \sqrt[n]{b}=a \cdot b^{\frac{1}{n}}=(a^n)^{\frac{1}{n}} \cdot b^{\frac{1}{n}}= (a^n \cdot b)^{\frac{1}{n}}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/7/9/3/793321a371ba1c1c188fd5e877399640.png)
![\sqrt[4]{3} - \sqrt[4]{243}](/wikipedia/images/math/e/6/6/e66fc6d8653c96dff0e3c0b95dc93b55.png)

