Arquímedes

De Wikipedia

(Diferencia entre revisiones)

Revisión actual

Arquímedes, por Domenico Fetti (1620).

Arquímedes (Siracusa, Sicilia), (287 a.C. - 212 a.C.), matemático y geómetra griego. Considerado el más notable científico y matemático de la antigüedad, es recordado por el Principio de Arquímedes y por sus aportes a la cuadratura del círculo, el estudio de la palanca, el tornillo de Arquímedes, la espiral de Arquímedes y otros aportes a la matemática, la ingeniería y la geometría.

[editar]

Biografía

Hijo del astrónomo Fidias, quien probablemente le introdujo en las matemáticas, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes; a este último dedicó Arquímedes su Método. Regresó luego a Siracusa, donde se dedicó de lleno al trabajo científico.

Durante el asedio de Siracusa por el general romano Marcelo, Arquímedes, a pesar de no ostentar cargo oficial alguno, se puso a disposición de Hierón, llevando a cabo prodigios en la defensa de su ciudad natal, pudiéndose afirmar que él sólo sostuvo la plaza contra el ejército romano. Entre la maquinaria de guerra cuya invención se le atribuye está la catapulta y un sistema de espejos y lentes que incendiaba los barcos enemigos al concentrar los rayos del Sol; según algunos historiadores, era suficiente ver asomar tras las murallas algún soldado con cualquier objeto que despidiera reflejos brillantes para que cundiera la alarma entre el ejército sitiador. Sin embargo, los confiados habitantes de Siracusa, teniéndose a buen recaudo bajo la protección de Arquímedes, descuidaron sus defensas, circunstancia que fue aprovechada por los romanos para entrar al asalto en la ciudad.

A pesar de las órdenes del cónsul Marco Claudio Marcelo de respetar la vida del sabio, durante el asalto, un soldado que le encontró abstraído en la resolución de algún problema, quizá creyendo que los brillantes instrumentos que portaba eran de oro, o irritado porque no contestaba a sus preguntas, le atravesó con su espada causándole la muerte. Otros datos dicen que, haciendo operaciones en la playa, unos soldados romanos pisaron sus cálculos, cosa que acabó en discusión y la muerte por espadazo por parte de los romanos. Se dice que sus últimas palabras fueron "no molestes a mis círculos".

La obra Sobre la esfera y el cilindro fue su teorema favorito, que por expreso deseo suyo se grabó sobre su tumba.

[editar]

Obra

Aunque probablemente su contribución científica más conocida sea el principio de la hidrostática que lleva su nombre, el Principio de Arquímedes, no fueron menos notables sus disquisiciones acerca de la cuadratura del círculo, el descubrimiento de la relación aproximada entre la circunferencia y su diámetro, relación que se designa hoy día con la letra griega Pi ( $π$ ).

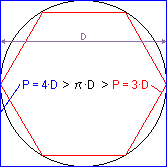
Arquímedes demostró que el lado del hexágono regular inscrito en un círculo es igual al radio de dicho círculo, así como que el lado del cuadrado circunscrito a un círculo es igual al diámetro de dicho círculo. De la primera proposición dedujo que el perímetro del hexágono inscrito era 3 veces el diámetro de la circunferencia, mientras que de la segunda dedujo que el perímetro del cuadrado circunscrito era 4 veces el diámetro de la circunferencia.

Afirmó, además, que toda línea cerrada envuelta por otra es de menor longitud que ésta, por lo que la circunferencia debía ser mayor que tres diámetros pero menor que cuatro. Por medio de sucesivas inscripciones y circunscripciones de polígonos regulares llegó a determinar el valor aproximado de $π$ como:

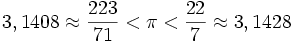
$3,1408 \approx \frac{223}{71} < \pi < \frac{22}{7} \approx 3,1428$

Con los rudimentarios medios de los que disponía el sabio griego, el error absoluto que cometió en el cálculo de π resultó ser inferior a una milésima (0,0040 %).

Sin embargo, Arquímedes es más conocido por enunciar el principio que lleva su nombre:

Principio de Arquímedes: todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.

Cuenta la historia que Hierón, el antes citado monarca de Siracusa, hizo entrega a un platero de la ciudad de ciertas cantidades de oro y plata para el labrado de una corona. Finalizado el trabajo, Hierón, desconfiado de la honradez del artífice y aún reconociendo la calidad artística de la obra, solicitó a Arquímedes que, conservando la corona en su integridad, determinase la ley de los metales con el propósito de comprobar si el artífice la había rebajado, guardándose para sí parte de lo entregado impulsado por la avaricia, la misma, con seguridad, que al propio Popin impelía a realizar semejante comprobación.

Preocupado Arquímedes por el problema, al que no encontraba solución, un buen día al sumergirse en el baño advirtió, como tantas veces con anterioridad, que a causa de la resistencia que el agua opone, el cuerpo parece pesar menos, hasta el punto que en alguna ocasión incluso es sostenido a flote sin sumergirse. Pensando en ello llegó a la conclusión que al entrar su cuerpo en la bañera, ocupaba un lugar que forzosamente dejaba de ser ocupado por el agua, y adivinó que lo que él pesaba de menos era precisamente lo que pesaba el agua que había desalojado.

Dando por resuelto el problema que tanto le había preocupado fue tal su excitación que, desnudo como estaba, saltó de la bañera y se lanzó por las calles de Siracusa al grito de ¡Eureka! ¡Eureka! (¡Lo encontré! ¡Lo encontré!). Procedió entonces Arquímedes a pesar la corona en el aire y en el agua verificando que en efecto, su densidad no correspondía a la que hubiera resultado de emplear el artífice todo el oro y la plata entregados y determinando, en consecuencia, que éste había estafado al Rey.

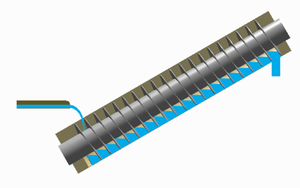
Tornillo de Arquímedes.

No se agota con esta anécdota el talento de Arquímedes que, además, se anticipó al descubrimiento del cálculo integral con sus estudios acerca de las áreas y volúmenes de figuras sólidas curvadas y de áreas de figuras planas; realizó un exhaustivo estudio de la espiral uniforme, conocida como espiral de Arquímedes; determinó el resultado de la serie geométrica de razón 1/4, el más antiguo del que se tiene noticia; creó un sistema numérico posicional para escribir números muy grandes; inventó una máquina para la elevación de agua, el tornillo de Arquímedes, así como la balanza que lleva su nombre; enunció la ley de la palanca lo que le llevó a proferir la célebre frase Dadme un punto de apoyo y moveré el mundo; inventó la polea compuesta, basada en el principio de la palanca, empleándola para mover un gran barco para sorpresa del escéptico Hierón.

Para él, su mayor descubrimiento fue demostrar que el volumen de una esfera es dos tercios del volumen del cilindro que la circunscribe, descubrimiento que pidió que fuera grabado en su tumba, según cuenta Plutarco. Cuarenta años después, el historiador romano Cicerón encontró la tumba gracias al grabado. Actualmente la tumba está otra vez perdida.

[editar]

Escritos

Arquímedes fue autor de numerosas obras de variada temática en las que destaca el rigor de sus demostraciones geométricas, razón por la que es considerado el más notable científico y matemático de la Antigüedad. Aunque muchos de sus escritos se perdieron en la destrucción de la Biblioteca de Alejandría, han llegado hasta la actualidad a través de las traducciones latinas y árabes. Aquí se indican algunas de ellas:

El arenario.
La medida del círculo.
De la esfera y el cilindro.
De la cuadratura.
De la parábola.
De los esferoides y conoides.
De las espirales.
Determinación de los centros de gravedad en las líneas y en los planos.
Del equilibrio de los cuerpos en los fluidos.
El método.
De los métodos mecánicos en la geometría (Palimpsesto de Arquímedes).
Sobre los cuerpos flotantes.

Obtenido de "http://maralboran.org/wikipedia/index.php/Arqu%C3%ADmedes"

Categorías: Matemáticas | Historia de las Matemáticas | Matemáticos

-[[Image:arquimedes.jpg|thumb|right|Arquímedes]]
 [[Imagen:Domenico-Fetti Archimedes 1620.jpg|thumb|''Arquímedes'', por Domenico Fetti (1620).|right]]
 '''Arquímedes''' (Siracusa, Sicilia), (287 a.C. - 212 a.C.), matemático y geómetra griego. Considerado el más notable científico y matemático de la antigüedad, es recordado por el Principio de Arquímedes y por sus aportes a la [[cuadratura del círculo]], el estudio de la palanca, el tornillo de Arquímedes, la [[espiral de Arquímedes]] y otros aportes a la matemática, la ingeniería y la geometría.

Arquímedes

De Wikipedia

Revisión actual

Biografía

Obra

Escritos

Vistas

Herramientas personales

Menú

Buscar

Herramientas