Las matemáticas en la Europa medieval (c. 500-1400)

De Wikipedia

Revisión de 19:12 16 dic 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior		Revisión actual Coordinador (Discusión | contribuciones) (→Videos)
Línea 5:		Línea 5:
	==Temprana Edad Media (c. 500-1100)==		==Temprana Edad Media (c. 500-1100)==
-	Boethius siempre tuvo un lugar para las matemáticas en el plan de estudios cuando se acuñó el término "quadrivium" para describir el estudio de la aritmética, la geometría, la astronomía, y la música. Él escribió ''De institutione arithmetica'', una traducción libre de la ''Introducción a la Aritmética'' del griego de Nicomachus; ''De institutione musica'', también derivados de fuentes griegas, y una serie de extractos de la Geometría de [[Euclides]]. Sus obras fueron teóricas, más que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.	+	Boethius siempre tuvo un lugar para las matemáticas en el plan de estudios cuando se acuñó el término "quadrivium" para describir el estudio de la aritmética, la geometría, la astronomía, y la música. Él escribió ''De institutione arithmetica'', una traducción libre del griego de la ''Introducción a la Aritmética'' de Nicomachus; ''De institutione musica'', también procedente de fuentes griegas, y una serie de extractos de la Geometría de [[Euclides]]. Sus obras fueron teóricas, más que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.
	==Renacimiento de las matemáticas en Europa (1100-1400)==		==Renacimiento de las matemáticas en Europa (1100-1400)==
-	En el siglo XII, los estudiosos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluyendo el de Al-Khwarizmi, ''al-Jabr wa-al-Muqabilah'', traducido al latín por Robert de Chester, y el texto completo de los [[Elementos]] de [[Euclides]], traducidos en varias versiones por Adélard de Bath, Herman de Carintia, y Gerard de Cremona.	+	En el siglo XII, los estudiosos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluyendo el ''al-Jabr wa-al-Muqabilah'' del matemático [[Al-Khwarizmi]], traducido al latín por Robert de Chester, y el texto completo de los ''Elementos'' de [[Euclides]], traducidos en varias versiones por Adélard de Bath, Herman de Carintia, y Gerard de Cremona.
-	Estas nuevas fuentes provocaron una renovación de la matemática. [[Fibonacci]], con el ''Liber Abaci'', escrito en 1202 y actualizado en 1254, elaboró las primeras matemáticas significativas en Europa desde la época de Eratóstenes, un lapsus de más de un millar de años. Su trabajo introdujo la numeración arábico-hindú en Europa, y se debatieron muchos otros problemas matemáticos.	+	Estas nuevas fuentes provocaron una renovación de la matemática. [[Fibonacci]], con el ''Liber Abaci'', escrito en 1202 y actualizado en 1254, elaboró las primeras matemáticas significativas en Europa desde la época de [[Eratóstenes]], un lapsus de más de un millar de años. Su trabajo introdujo la numeración arábico-hindú en Europa, y se debatieron muchos otros problemas matemáticos.
	El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Un área importante que contribuyó al desarrollo de la matemática fue el del análisis del movimiento local.		El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Un área importante que contribuyó al desarrollo de la matemática fue el del análisis del movimiento local.
Línea 18:		Línea 18:
	<center><math>v = log \left ( \cfrac{F}{R} \right )</math></center>		<center><math>v = log \left ( \cfrac{F}{R} \right )</math></center>
	{{p}}		{{p}}
-	Bradwardine del análisis es un ejemplo de la transferencia de un matemático técnica utilizada por al-Kindi y Arnald de Villanova para cuantificar la naturaleza de los medicamentos compuestos diferentes a un problema físico [37].	+	El análisis de Bradwardine es un ejemplo de como la técnica utilizada por al-Kindi y Arnald de Villanova para cuantificar la naturaleza de los medicamentos compuestos, se traslada a un problema físico diferente.
-	Uno de los 14 al siglo Oxford Calculadoras, William HEYTESBURY, que carecen de cálculo diferencial y el concepto de límites, propuesto para medir la velocidad instantánea "de la ruta que se describe por [un cuerpo] ... si se traslada de manera uniforme en la misma grado de rapidez con que se mueve en ese instante dado "[38].	+	Uno de los calculadores de Oxford del siglo XIV, William Heytesbury, carente de cálculo diferencial y del concepto de límite, propuso para medir la velocidad instantánea "de la ruta que describe un cuerpo si se traslada de manera uniforme con la misma rapidez con que se mueve en ese instante dado"
-	HEYTESBURY y otros determina matemáticamente la distancia recorrida por un cuerpo en movimiento uniformemente acelerado (que se resolvería mediante una simple integración), afirmando que "un cuerpo en movimiento de manera uniforme en la adquisición o incremento que perder [de velocidad] recorrerá en algunos un momento dado [ distancia] completamente igual a la que sería atravesar si se desplazan continuamente por el mismo tiempo con la media de grado [de velocidad] "[39].	+	Heytesbury y otros determinaron matemáticamente la distancia recorrida por un cuerpo en movimiento uniformemente acelerado (lo que nosotros hoy resolveríamos mediante una simple integral), afirmando que "un cuerpo en movimiento que adquiere o pierde de manera uniforme ese incremento de velocidad recorrerá en un momento dado una distancia completamente igual a la que recorrería si se desplazase de forma continua durante el mismo tiempo con la media de la velocidad".
-	Nicole Oresme de la Universidad de París y el italiano Giovanni di Casali independiente siempre las manifestaciones gráficas de esta relación, afirmando que el área bajo la línea que representa la aceleración constante, representada la distancia total recorrida. [40] En un comentario posterior sobre matemáticas de la Geometría de Euclides , Oresme hizo un análisis más detallado análisis general en el que demostró que un cuerpo voluntad adquirir en cada incremento de tiempo un incremento de cualquier calidad que aumenta a medida que los números impares. Desde Euclides, ha demostrado la suma de los números impares son los números cuadrados, el total de la calidad adquirida por el cuerpo aumenta a medida que el cuadrado del tiempo	+	Nicole Oresme de la Universidad de París y el italiano Giovanni di Casali proporcionaron de manera independientemente demostraciones de esta relación, afirmando que el área bajo la línea que representa la aceleración constante, representaba la distancia total recorrida. En un comentario posterior sobre las matemáticas de la Geometría de Euclides , Oresme hizo un más detallado análisis general en el que demostró que un cuerpo adquirirá en cada sucesivo incremento de tiempo un incremento de cualquier cualidad que aumenta como los números impares. Como Euclides había demostrado que la suma de los números impares son los números cuadrados, el total de la calidad adquirida por el cuerpo aumenta como el cuadrado del tiempo
		+	==Videos==
		+	{{Video_enlace2
		+	|titulo1=Fibonacci. La magia de los números
		+	|duracion=16´
		+	|url1=http://maralboran.org/web_ma/videos/fibonacci/fibonacci.htm
		+	|titulo2=Acceso por red TIC
		+	|url2=http://c0/helvia/aula/archivos/repositorio//0/112/html/index.htm
		+	|sinopsis=Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
		+	}}
		+	{{Video_enlace2
		+	|titulo1=La divina proporción: el número phi
		+	|duracion=6'
		+	|url1=http://maralboran.org/web_ma/videos/ladivinaproporcion/ladivinaproporcion.html
		+	|titulo2=Acceso por red TIC
		+	|url2=http://c0/helvia/aula/archivos/repositorio//0/92/html/index.htm
		+	|sinopsis=
		+	}}
	[[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]]		[[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]]

---

Revisión actual

<<< Historia de las Matemáticas

El interés de los europeos medievales en las matemáticas fue impulsado por preocupaciones muy diferentes de las de los matemáticos modernos. Un elemento de conducción fue la creencia de que la matemática proporcionaba la clave para comprender el orden de la naturaleza, a menudo justificada por Platón de Timeo y el pasaje de la Biblia en el que Dios había "ordenado todas las cosas en medida, número y peso".

Temprana Edad Media (c. 500-1100)

Boethius siempre tuvo un lugar para las matemáticas en el plan de estudios cuando se acuñó el término "quadrivium" para describir el estudio de la aritmética, la geometría, la astronomía, y la música. Él escribió De institutione arithmetica, una traducción libre del griego de la Introducción a la Aritmética de Nicomachus; De institutione musica, también procedente de fuentes griegas, y una serie de extractos de la Geometría de Euclides. Sus obras fueron teóricas, más que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.

Renacimiento de las matemáticas en Europa (1100-1400)

En el siglo XII, los estudiosos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluyendo el al-Jabr wa-al-Muqabilah del matemático Al-Khwarizmi, traducido al latín por Robert de Chester, y el texto completo de los Elementos de Euclides, traducidos en varias versiones por Adélard de Bath, Herman de Carintia, y Gerard de Cremona.

Estas nuevas fuentes provocaron una renovación de la matemática. Fibonacci, con el Liber Abaci, escrito en 1202 y actualizado en 1254, elaboró las primeras matemáticas significativas en Europa desde la época de Eratóstenes, un lapsus de más de un millar de años. Su trabajo introdujo la numeración arábico-hindú en Europa, y se debatieron muchos otros problemas matemáticos.

El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Un área importante que contribuyó al desarrollo de la matemática fue el del análisis del movimiento local. Thomas Bradwardine propone que la velocidad (v) aumenta en progresión aritmética mientras que la razón entre la fuerza (F) y la resistencia (R) aumentan en progresión geométrica. Bradwardine expresó esto por medio de una serie de ejemplos concretos, pero, aunque el logaritmo todavía no se había concebido, podemos expresar su conclusión anacrónicamente de la siguiente forma:

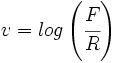
El análisis de Bradwardine es un ejemplo de como la técnica utilizada por al-Kindi y Arnald de Villanova para cuantificar la naturaleza de los medicamentos compuestos, se traslada a un problema físico diferente.

Uno de los calculadores de Oxford del siglo XIV, William Heytesbury, carente de cálculo diferencial y del concepto de límite, propuso para medir la velocidad instantánea "de la ruta que describe un cuerpo si se traslada de manera uniforme con la misma rapidez con que se mueve en ese instante dado"

Heytesbury y otros determinaron matemáticamente la distancia recorrida por un cuerpo en movimiento uniformemente acelerado (lo que nosotros hoy resolveríamos mediante una simple integral), afirmando que "un cuerpo en movimiento que adquiere o pierde de manera uniforme ese incremento de velocidad recorrerá en un momento dado una distancia completamente igual a la que recorrería si se desplazase de forma continua durante el mismo tiempo con la media de la velocidad".

Nicole Oresme de la Universidad de París y el italiano Giovanni di Casali proporcionaron de manera independientemente demostraciones de esta relación, afirmando que el área bajo la línea que representa la aceleración constante, representaba la distancia total recorrida. En un comentario posterior sobre las matemáticas de la Geometría de Euclides , Oresme hizo un más detallado análisis general en el que demostró que un cuerpo adquirirá en cada sucesivo incremento de tiempo un incremento de cualquier cualidad que aumenta como los números impares. Como Euclides había demostrado que la suma de los números impares son los números cuadrados, el total de la calidad adquirida por el cuerpo aumenta como el cuadrado del tiempo

Videos