Algunos límites importantes (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:44 12 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:16 12 ene 2009 Coordinador (Discusión | contribuciones) (→El número áureo, <math>\phi \;</math>) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| ==El número ''e''== | ==El número ''e''== | ||
| ==El número áureo, <math>\phi \;</math>== | ==El número áureo, <math>\phi \;</math>== | ||
| + | {{Teorema|titulo=''La sucesión de Fibonacci y el número áureo'' | ||
| + | |enunciado= | ||
| + | Si a partir de la '''sucesión de [[Fibonacci]]''' (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...), construimos, por recurrencia, la sucesión <math>b_n=\cfrac{a_{n+1}}{a_n}</math>, se cumple que: | ||
| + | <center><math>lim \ b_n=lim \ \cfrac{a_{n+1}}{a_n}= \frac{1 + \sqrt{5}}{2} = \phi = 1.618 \cdots</math> ('''número áureo''')</center> | ||
| + | |demo= | ||
| + | Lo siguiente no es una demostración, sino una comprobación: | ||
| + | |||
| + | En efecto, si en la sucesión de Fibonacci | ||
| + | |||
| + | <center><math>1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89, \cdots</math></center> | ||
| + | |||
| + | dividimos cada término entre el anterior, tenemos: | ||
| + | |||
| + | <center><math>\cfrac{1}{1},\ \cfrac{2}{1},\ \cfrac{3}{2},\ \cfrac{5}{3},\ \cfrac{8}{5},\ \cfrac{13}{8},\ \cdots</math></center> | ||
| + | |||
| + | que expresada con decimales nos da: | ||
| + | |||
| + | <center><math>1,\ 2,\ 1.5,\ 1.66,\ 1.6,\ 1.625,\ 1.615 \cdots \rightarrow \phi</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video | ||
| + | |titulo=La divina proporción. El número Phi (<math>\phi</math>) | ||
| + | |sinopsis=Documental sobre la historia del número Phi <math>(\phi)</math> y la divina proporción. | ||
| + | |duracion=6´ | ||
| + | |video= | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/videos/ladivinaproporcion/ladivinaproporcion.html | ||
| + | width=100% | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/videos/ladivinaproporcion/ladivinaproporcion.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | <center>[http://c0/helvia/aula/archivos/repositorio//0/92/html/index.htm '''Click''' aquí para enlace desde servidor TIC]</center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Web | ||
| + | |titulo=Phi, el número de oro | ||
| + | |descripcion=A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz. | ||
| + | |enlace=[http://w3.cnice.mec.es/eos/MaterialesEducativos/secundaria/matematicas/phi/index.htm Phi, el número de oro] | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 17:16 12 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Suma de los términos de una progresión geométrica
El número e
El número áureo,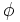 
La sucesión de Fibonacci y el número áureo
Si a partir de la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...), construimos, por recurrencia, la sucesión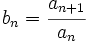 
, se cumple que:
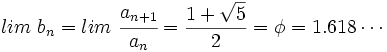(número áureo)Demostración:
Lo siguiente no es una demostración, sino una comprobación:
En efecto, si en la sucesión de Fibonacci
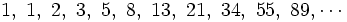
dividimos cada término entre el anterior, tenemos:
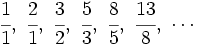
que expresada con decimales nos da:
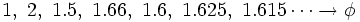
Video: La divina proporción. El número Phi (φ) (6´)
Sinopsis:
Documental sobre la historia del número Phi (φ) y la divina proporción.
Web: [Phi, el número de oro Phi, el número de oro]
Descripción:
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
