Concepto de sucesión (1ºBach)
De Wikipedia
| Revisión de 17:22 12 ene 2009 Coordinador (Discusión | contribuciones) (→La sucesión de Fibonacci y el número áureo) ← Ir a diferencia anterior |
Revisión de 17:24 12 ene 2009 Coordinador (Discusión | contribuciones) (→La sucesión de Fibonacci y el número áureo) Ir a siguiente diferencia → |
||
| Línea 27: | Línea 27: | ||
| '''a) Sucesión de Fibonacci:''' | '''a) Sucesión de Fibonacci:''' | ||
| - | [[Imagen:conejos_fibonacci.jpg|right|230px]] | + | [[Imagen:conejos_fibonacci.jpg|right|250px]] |
| *Valor inicial: 1 pareja | *Valor inicial: 1 pareja | ||
| *Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera) | *Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera) | ||
| - | *Mes 2: 2 parejas (Primera vez que se reproduce) | + | *Mes 2: 2 parejas (primera vez que se reproduce) |
| *Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes) | *Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes) | ||
| *Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no) | *Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no) | ||
| - | *Mes 5: 8 parejas (Se reproducen las 3 primeras parejas, las otras dos no) | + | *Mes 5: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no) |
| - | *Mes 6: 13 parejas (Se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no) | + | *Mes 6: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no) |
| Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores: | Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores: | ||
| Línea 45: | Línea 45: | ||
| <center><math>\cfrac{1}{1},\ \cfrac{2}{1},\ \cfrac{3}{2},\ \cfrac{5}{3},\ \cfrac{8}{5},\ \cfrac{13}{8},\ \cdots</math></center> | <center><math>\cfrac{1}{1},\ \cfrac{2}{1},\ \cfrac{3}{2},\ \cfrac{5}{3},\ \cfrac{8}{5},\ \cfrac{13}{8},\ \cdots</math></center> | ||
| - | {{b}} | + | |
| + | que expresada con decimales nos da: | ||
| + | |||
| <center><math>1,\ 2,\ 1.5,\ 1.66,\ 1.6,\ 1.625,\ 1.615 \cdots \rightarrow \phi</math></center> | <center><math>1,\ 2,\ 1.5,\ 1.66,\ 1.6,\ 1.625,\ 1.615 \cdots \rightarrow \phi</math></center> | ||
| }} | }} | ||
Revisión de 17:24 12 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Concepto de sucesión
Se llama sucesión a un conjunto ordenado de números. A los elementos de la sucesión se les llama términos. Los términos se representan con una misma letra y un subíndice que indica el lugar que ocupa en la sucesión.
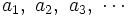
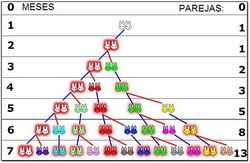
La sucesión de Fibonacci y el número áureo
Ejemplo: La sucesión de Fibonacci y el número áureo
- El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
- a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
- b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo, phi (
):
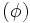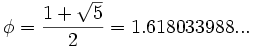
a) Sucesión de Fibonacci:
- Valor inicial: 1 pareja
- Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera)
- Mes 2: 2 parejas (primera vez que se reproduce)
- Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes)
- Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 5: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 6: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores:
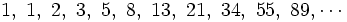
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos:
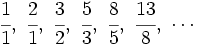
que expresada con decimales nos da:
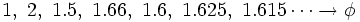
Término general de una sucesión
Se llama término general de una sucesión, y se simboliza por 
, a la expresión matemática que sirve para calcular cualquier término de la sucesión. Para ello, sustituiremos n en la expresión del término general por el índice del término que queramos averiguar.
Hay veces que el término general se puede expresar mediante una función: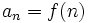 
.
Otras veces, cada término de la sucesión se obtiene a aprtir de operaciones con otros términos anteriores. A estas sucesiones se les llama recurrentes.
Ejemplo: Término general de una sucesión
- Halla el término general de las siguientes sucesiones:
- a) 1, 4, 9, 16, 25, 36, ...
- b) 2, 4, 8, 16, 32, 64, ...
- c) 1, 1, 2, 3, 5, 8, 13, ...
a)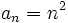 
b)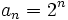 
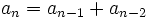(es recurrente)
