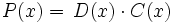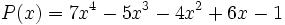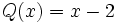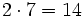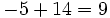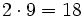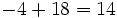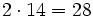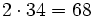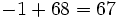Factorización de polinomios (1ºBach)
De Wikipedia
| Revisión de 09:01 13 ene 2009 Coordinador (Discusión | contribuciones) (→Procedimientos para la factorización de polinomios de grado mayor que 2) ← Ir a diferencia anterior |
Revisión de 09:04 13 ene 2009 Coordinador (Discusión | contribuciones) (→División de un polinomio por (x-a). Regla de Ruffini) Ir a siguiente diferencia → |
||
| Línea 138: | Línea 138: | ||
| ---- | ---- | ||
| Divide los polinomios usando la regla de [[Ruffini]]: | Divide los polinomios usando la regla de [[Ruffini]]: | ||
| - | :<math> P(x)=7x^4-5x^3-4x^2+6x-1\,\! </math> | + | ::<math> P(x)=7x^4-5x^3-4x^2+6x-1\,\! </math> |
| - | :<math> Q(x)=x-2\,\! </math> | + | ::<math> Q(x)=x-2\,\! </math> |
| <div class="NavFrame" style="background: white; border: 0px solid #aaaaaa; padding:3px; margin-bottom:0em; margin-left:0em;"> | <div class="NavFrame" style="background: white; border: 0px solid #aaaaaa; padding:3px; margin-bottom:0em; margin-left:0em;"> | ||
| Línea 193: | Línea 193: | ||
| </div> | </div> | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Procedimientos para la factorización de polinomios de grado mayor que 2=== | ===Procedimientos para la factorización de polinomios de grado mayor que 2=== | ||
| *Siempre que se pueda, sacaremos <math>x\;</math> '''factor común'''. | *Siempre que se pueda, sacaremos <math>x\;</math> '''factor común'''. | ||
Revisión de 09:04 13 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Divisibilidad de polinomios
Polinomios múltiplos y divisores
La divisibilidad en el conjunto de los polinomios es muy similar a la .
Un polinomio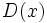 
es divisor de otro, 
y lo representaremos por 
, si la división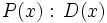 
es exacta. Es decir, cuando
|
|
En tal caso, diremos que es divisible por 
. También diremos que es un múltiplo de .
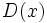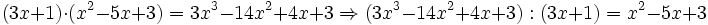
La divisibilidad de polinomios es semejante a la divisibilidad con números enteros. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de máximo común divisor, mínimo común múltiplo e irreducibilidad son similares a los correspondientes conceptos numéricos.
Polinomios irreducibles
Un polinomio es irreducible cuando ningún polinomio de grado inferior es divisor suyo.
Son polinomios irreducibles, entre otros:
- Los de primer grado:
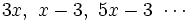
- Los de segundo grado sin raíces:
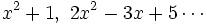
Factorización de polinomios
Factorizar un polinomio es descomponerlo en producto de polinomios con el menor grado posible.
Factorización de polinomios de grado 2
Factorización de polinomios de segundo grado
Un polinomio de segundo grado,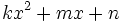 
, con raíces rales, 
y 
, se puede factorizar de la forma
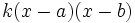
- El polinomio
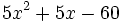tiene dos raíces: 
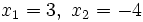, que se obtienen de resolver la ecuación de segundo grado 
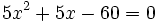. Entonces:
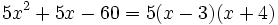
- El polinomio incompleto de grado 3,
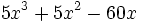, se puede descomponer de la siguiente manera:
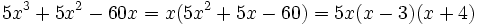
- (Observa que primero hemos sacado factor común
y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
División de un polinomio por (x-a). Regla de Ruffini
Regla de Ruffini
La Regla de Ruffini nos permite dividir un polinomio entre un binomio de la forma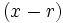 
, siendo 
un número entero.
Debemos esta regla al matemático italiano Paolo Ruffini,
Vamos a dividir el polinomio
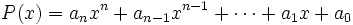
entre el binomio
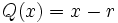
para obtener el cociente
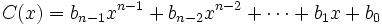
y el resto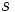 
.
1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de P(x) y los escribimos ordenados. Entonces escribimos r en la parte inferior izquierda del eje, encima de la línea:
| an an-1 ... a1 a0
|
r |
----|---------------------------------------------------------
|
|
2. Pasamos el coeficiente más pegado a la izquierda (an) abajo, justo debajo de la línea para obtener el primero de los coeficientes b:
| an an-1 ... a1 a0
|
r |
----|---------------------------------------------------------
| an
|
| = bn-1
|
3. Multiplicamos el número más pegado a la derecha debajo de la línea por r y lo escribimos sobre la línea en la primera posición de la derecha:
| an an-1 ... a1 a0
|
r | bn-1r
----|---------------------------------------------------------
| an
|
| = bn-1
|
4. Añadimos los dos valores que hemos puesto en la misma columna:
| an an-1 ... a1 a0
|
r | bn-1r
----|---------------------------------------------------------
| an an-1+(bn-1r)
|
| = bn-1 = bn-2
|
5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:
| an an-1 ... a1 a0
|
r | bn-1r ... b1r b0r
----|---------------------------------------------------------
| an an-1+(bn-1r) ... a1+b1r a0+b0r
|
| = bn-1 = bn-2 ... = b0 = s
|
Los valores b son los coeficientes del polinomio resultante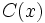 
, el grado será menor que el grado de 
. El resto será .
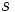Ejemplo: Regla de Ruffini
Divide los polinomios usando la regla de Ruffini:
7 -5 -4 6 -1 2 14 18 28 68 7 9 14 34 67 Operaciones: El resultado significa que el cociente de la división
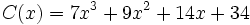y el resto es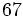 
-
Procedimientos para la factorización de polinomios de grado mayor que 2
- Siempre que se pueda, sacaremos factor común.
- Mediante la regla de Ruffini buscaremos las raíces enteras del polinomio, que se hallan entre los divisores del término independiente. Así, si encontramos una raíz
de un polinomio , tendremos que 
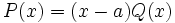, donde 
tiene un grado menos que .
- Si es un polinomio bicuadrado, ax^4+bx^2+c\;, podremos hallarle las raices resolviendo la ecuación bicuadrada que resulta de igualarlo a cero.
- Si un polinomio de grado mayor que 2 no puede factorizarse usando los procedimientos anteriores, es poco probable que podamos hacerlo con lo sconocimientos que tenemos.
