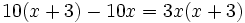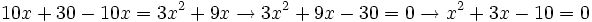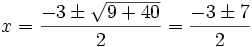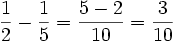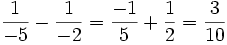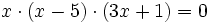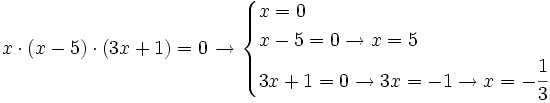Resolución de ecuaciones (1ºBach)
De Wikipedia
| Revisión de 17:49 13 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:52 13 ene 2009 Coordinador (Discusión | contribuciones) (→Ecuaciones bicuadradas) Ir a siguiente diferencia → |
||
| Línea 106: | Línea 106: | ||
| <center>[http://maralboran.org/web_ma/descartes/4b_eso/Ecuaciones2grado/eg21_2.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/4b_eso/Ecuaciones2grado/eg21_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| }} | }} | ||
| + | |||
| ==Ecuaciones bicuadradas== | ==Ecuaciones bicuadradas== | ||
| - | [[Otros Tipos de Ecuaciones (4ºESO-B)#Ecuaciones bicuadradas|Ver Ecuaciones bicuadradas en 4º ESO]] | + | {{Caja_Amarilla|texto= |
| - | == | + | Las '''ecuaciones bicuadradas''' Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma |
| + | <center><math>ax^4 + bx^2 +c = 0\,\!</math></center> | ||
| + | |||
| + | El truco para resolverlas es hacer el cambio de variable <math>x^2=y\,\!</math>. Entonces, la ecuación quedará como una de segundo grado | ||
| + | |||
| + | <center><math>ay^2 + by + c = 0 \,\!</math></center> | ||
| + | |||
| + | Una vez resuelta esta ecuación en <math>y\;</math>, tenemos que averiguar el valor de la <math>x\;</math>. Para ello desharemos el cambio de variable, haciendo <math>x=\pm \sqrt{y}</math>. En consecuencia, las soluciones <math>y<0\,\!</math>, las rechazaremos, ya que no darán solución para la <math>x\,\!</math>, quedándonos sólo con las soluciones de <math>y\,\!</math> no negativas, cada una de las cuales dará dos soluciones para la <math>x\,\!</math>.}} | ||
| + | {{p}} | ||
| + | |||
| + | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones bicuadradas'' | ||
| + | |enunciado=Resuelve las ecuaciones: | ||
| + | ::a) <math>x^4 - 7x^2 + 6 = 0\;\! </math> | ||
| + | ::b) <math>x^4 - 3x^2 - 10 = 0\;\! </math> | ||
| + | ::c) <math>x^4 - 9x^2 = 0 \;\! </math> | ||
| + | |sol= | ||
| + | a) <math>x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6=0</math> | ||
| + | |||
| + | <math>y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}</math> | ||
| + | |||
| + | '''Soluciones:''' <math>-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!</math> | ||
| + | {{p}} | ||
| + | ---- | ||
| + | b) <math>x^4 - 3x^2 - 10 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-3y-10=0</math> | ||
| + | |||
| + | <math>y = \frac{3 \pm \sqrt{9+40}}{2}=\frac{3 \pm 7}{2} \rightarrow \begin{cases} y=-2 \rightarrow \mbox {No existe solucion para x} \\ y=5 \rightarrow x= \pm \sqrt 5 \end{cases}</math> | ||
| + | |||
| + | '''Soluciones:''' <math> -\sqrt 5,\, \sqrt 5\,\!</math> | ||
| + | {{p}} | ||
| + | ---- | ||
| + | c) <math>x^4 - 9x^2 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-9y=0</math> | ||
| + | |||
| + | <math> y(y-9)=0 \rightarrow \begin{cases} y=0 \rightarrow x= 0 \\ y=9 \rightarrow x= \pm \sqrt 9 = \pm 3 \end{cases}</math> | ||
| + | |||
| + | '''Soluciones:''' <math>0,\, -3,\, 3\,\!</math> | ||
| + | }} | ||
| + | |||
| + | ==Ecuaciones con la x en el denominador== | ||
| + | {{Caja_Amarilla|texto=Las ecuaciones que tienen la incógnita en el denominador, laspuedes resolver de forma análoga a las que tienen números en el denominador, es decir, haciendo el '''mínimo común múltiplo de los denominadores'''. A continuación se divide el m.c.m. entre cada denominador y se multiplica el resultado por su respectivo numerador, Esto se hace con los dos miembros de la ecuación.De esta forma desaparecen los denominadores y la ecuación resultante ya es más sencilla de resolver. | ||
| + | |||
| + | En estos procesos de multiplicar los miembros de la ecuación por polinomios, pueden aparecer soluciones falsas. Por tanto, al terminar, siempre debemos '''comprobar todas las posibles soluciones''' obtenidas. | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones con x en el denominador'' | ||
| + | |enunciado=Resuelve las ecuación: <math> \frac{1} {x}- \frac{1} {x+3} = \frac{3} {10} </math> | ||
| + | |sol=El m.c.m. de los denominadores es <math>10x(x+3)\,\!</math>. Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen: | ||
| + | |||
| + | :<math>10(x+3)-10x = 3x(x+3)\;</math> | ||
| + | |||
| + | Simplificamos la ecuación resultante: | ||
| + | |||
| + | :<math>10x+30-10x = 3x^2+9x \rightarrow 3x^2+9x-30 = 0 \rightarrow x^2+3x-10 = 0 | ||
| + | </math> | ||
| + | |||
| + | Y la resolvemos: | ||
| + | |||
| + | :<math>x = \frac{-3 \pm \sqrt{9+40}} {2} = \frac{-3 \pm 7} {2} | ||
| + | </math> | ||
| + | |||
| + | Hay dos soluciones: <math>x=2\;</math> y <math>x=-5\;</math>. Ambas se deben comprobar en la ecuación inicial y resultan ser válidas: | ||
| + | |||
| + | :<math> \frac{1} {2}- \frac{1} {5}= \frac{5-2} {10} = \frac{3} {10}</math> | ||
| + | :<math> \frac{1} {-5}- \frac{1} {-2}= \frac{-1} {5}+ \frac{1} {2} = \frac{3} {10}</math> | ||
| + | |||
| + | }} | ||
| + | |||
| + | ==Ecuaciones con radicales== | ||
| + | {{Caja_Amarilla|texto=Las '''ecuaciones con radicales''' son aquellas que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas. | ||
| + | |||
| + | Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que '''hacer la comprobación''' en la ecuación inicial para detectar y recharzar las que no sean válidas. | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones con radicales | ||
| + | |enunciado=Resuelve las ecuaciones: | ||
| + | ::a) <math>\sqrt{3x-5} +1=x\;\! </math> | ||
| + | |||
| + | ::b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4 \;\! </math> | ||
| + | |sol= | ||
| + | |||
| + | a) <math>\sqrt{3x-5} +1=x</math> | ||
| + | |||
| + | <math>\sqrt{3x-5}=x-1</math> | ||
| + | |||
| + | Se elevan al cuadrado los dos lados de la ecuación: | ||
| + | |||
| + | <math>3x-5=x^2-2x+1 \rightarrow x^2 -5x + 6 \rightarrow x_1=2 \ x_2=3 \,\!</math> | ||
| + | |||
| + | Comprobación: <math>\begin{cases} \sqrt{3 \cdot 2 - 5} + 1 = \sqrt{1} + 1 = 2 \ \mbox{valida} \\ \sqrt{3 \cdot 3 - 5} + 1 = \sqrt{4} + 1 = 3 \ \mbox{valida} \end{cases}</math> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4</math> | ||
| + | |||
| + | Despejamos la primera raíz (Podíamos haber empezado por la segunda) | ||
| + | |||
| + | <math>\sqrt{2x-3} = 4 - \sqrt{x+7}</math> | ||
| + | |||
| + | Se elevan al cuadrado los dos lados del igual | ||
| + | |||
| + | <math>2x-3 = 16 + (x+7) -8\sqrt{x+7}</math> | ||
| + | |||
| + | Aislamos la raíz | ||
| + | |||
| + | <math>x -26 = -8\sqrt{x+7}</math> | ||
| + | |||
| + | Se elevan al cuadrado los dos lados del igual | ||
| + | |||
| + | <math>x^2-52x+676=64(x+7) \rightarrow x^2-116x+228=0 \rightarrow x_1=2 \ x_2=114</math> | ||
| + | |||
| + | Comprobación <math>\begin{cases} x_1=2 \rightarrow \sqrt{2 \cdot 2 -3} \sqrt{2+7}=\sqrt{1}+\sqrt{9} = 1+3=4 \ \mbox{valida} \\ x_2=114 \rightarrow \sqrt{2 \cdot 114 - 3} + \sqrt{114+7}=15+11 \ne 4 \ \mbox{no valida} \end{cases}</math> | ||
| + | }} | ||
| + | |||
| + | ==Ecuaciones factorizadas== | ||
| + | |||
| + | {{Caja_Amarilla|texto= | ||
| + | Las '''ecuaciones factorizadas''' son ecuaciones del tipo: | ||
| + | <center> <math> (...) \cdot (...) \cdot (...) = 0 </math></center> | ||
| + | |||
| + | donde cada factor <math>(...)\;</math> es una expresión algebraica. | ||
| + | |||
| + | Como para que un producto sea cero basta con que uno de los factores sea cero, tenemos que igualar a cero cada factor y resolver la ecuación resultante. | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Ejemplo|titulo=Ejemplo: ''Ecuación factorizada'' | ||
| + | |enunciado=Resuelve la ecuación <math> x \cdot (x-5)\cdot (3x+1)=0\;\!</math> | ||
| + | |||
| + | |sol= | ||
| + | <math> x \cdot (x-5)\cdot (3x+1)=0\;\! \rightarrow \begin{cases} x = 0 | ||
| + | \\ x-5=0 \rightarrow x=5 \\ 3x+1=0 \rightarrow 3x=-1 \rightarrow x= -\cfrac{1} {3} | ||
| + | \end{cases}</math> | ||
| + | |||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 17:52 13 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
==Repaso de
Tabla de contenidos |
Ecuaciones de segundo grado
Ecuación de segundo grado
Una ecuación de segundo grado con una incógnita,  , es aquella que tiene la siguiente expresión, que llamaremos forma general.
, es aquella que tiene la siguiente expresión, que llamaremos forma general.
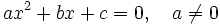
Resolución de la ecuación de segundo grado
Fórmula de la ecuación de segundo grado
Las soluciones de la ecuación de segundo grado son:
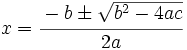
donde el signo 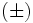 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 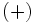 y otra con el signo
y otra con el signo 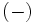 .
.
1. Se divide la ecuación por  :
:
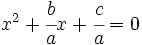
2. Se multiplica y divide por  el coeficiente de la
el coeficiente de la  :
:
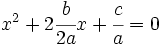
3. Se suma alos dos miembros de la igualdad 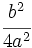 :
:
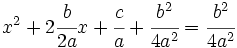
4. Se pasa restando a la derecha  :
:
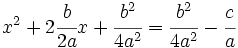
5. Observando que el lado izquierdo es el desarrollo de 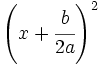 :
:
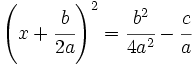
6. Se extrae la raíz cuadrada en ambos miembros:
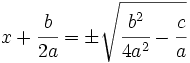
7. Se despeja x:
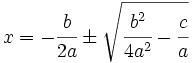
8. Se simplifica la expresión:
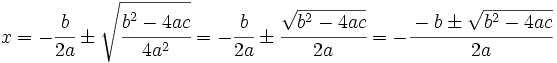
Ejemplo: Resolución de la ecuación de segundo grado
- Ejemplos de ecuaciones de segundo grado resueltas.
Pulsa "Inicio" para ver otros ejemplos:
Discriminante de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado a:
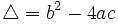
por tanto:
- Si
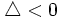 la ecuación no tiene solución.
la ecuación no tiene solución.
- Si
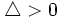 la ecuación tiene dos soluciones.
la ecuación tiene dos soluciones.
- Si
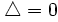 la ecuación tiene una solución (doble).
la ecuación tiene una solución (doble).
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado 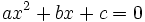 es incompleta, si ocurre uno de los siguientes casos:
es incompleta, si ocurre uno de los siguientes casos:
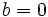 :
: 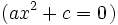
- En este caso las soluciones se obtienen despejando x:
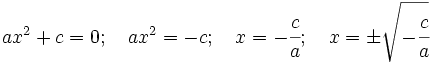
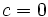 :
: 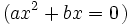
- En este caso, sacando factor común e igualando a cero cada factor:
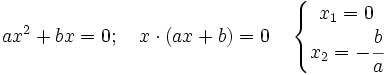
Ejemplo: Ecuaciones de segundo grado incompletas
- Ejemplos de ecuaciones de segundo grado incompletas resueltas.
Pulsa "INICIO" para ver otros ejemplos:
- Caso 1:
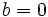 :
: 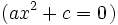
- Caso 2:
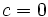 :
: 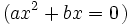
Ecuaciones bicuadradas
Las ecuaciones bicuadradas Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma
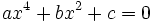
El truco para resolverlas es hacer el cambio de variable 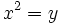 . Entonces, la ecuación quedará como una de segundo grado
. Entonces, la ecuación quedará como una de segundo grado
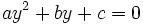
Una vez resuelta esta ecuación en  , tenemos que averiguar el valor de la
, tenemos que averiguar el valor de la  . Para ello desharemos el cambio de variable, haciendo
. Para ello desharemos el cambio de variable, haciendo 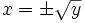 . En consecuencia, las soluciones
. En consecuencia, las soluciones 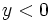 , las rechazaremos, ya que no darán solución para la
, las rechazaremos, ya que no darán solución para la 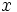 , quedándonos sólo con las soluciones de
, quedándonos sólo con las soluciones de 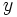 no negativas, cada una de las cuales dará dos soluciones para la
no negativas, cada una de las cuales dará dos soluciones para la 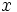 .
.
Ejemplo: Ecuaciones bicuadradas
Resuelve las ecuaciones:
- a)
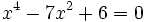
- b)
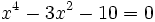
- c)
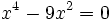
- a)
a) 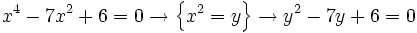
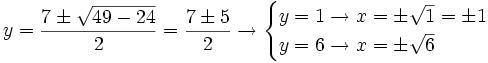
Soluciones: 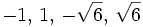
b) 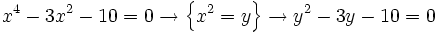
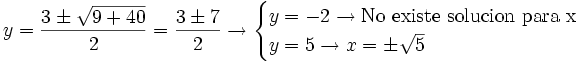
Soluciones: 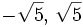
c) 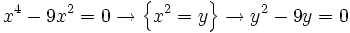
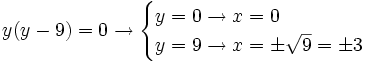
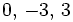
Ecuaciones con la x en el denominador
Las ecuaciones que tienen la incógnita en el denominador, laspuedes resolver de forma análoga a las que tienen números en el denominador, es decir, haciendo el mínimo común múltiplo de los denominadores. A continuación se divide el m.c.m. entre cada denominador y se multiplica el resultado por su respectivo numerador, Esto se hace con los dos miembros de la ecuación.De esta forma desaparecen los denominadores y la ecuación resultante ya es más sencilla de resolver.
En estos procesos de multiplicar los miembros de la ecuación por polinomios, pueden aparecer soluciones falsas. Por tanto, al terminar, siempre debemos comprobar todas las posibles soluciones obtenidas.
Ejemplo: Ecuaciones con x en el denominador
Resuelve las ecuación: 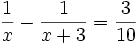
El m.c.m. de los denominadores es 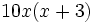 . Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen:
. Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen:
Simplificamos la ecuación resultante:
Y la resolvemos:
Hay dos soluciones:  y
y 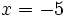 . Ambas se deben comprobar en la ecuación inicial y resultan ser válidas:
. Ambas se deben comprobar en la ecuación inicial y resultan ser válidas:
Ecuaciones con radicales
Las ecuaciones con radicales son aquellas que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.
Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que hacer la comprobación en la ecuación inicial para detectar y recharzar las que no sean válidas.
Ejemplo: Ecuaciones con radicales
Resuelve las ecuaciones:
- a)
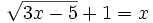
- a)
- b)
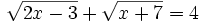
- b)
a) 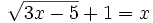
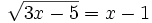
Se elevan al cuadrado los dos lados de la ecuación:
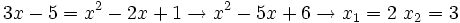
Comprobación: 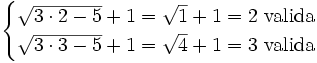
b) 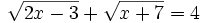
Despejamos la primera raíz (Podíamos haber empezado por la segunda)
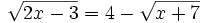
Se elevan al cuadrado los dos lados del igual
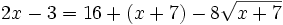
Aislamos la raíz
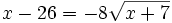
Se elevan al cuadrado los dos lados del igual
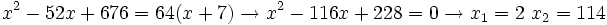
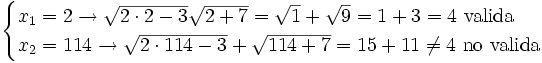
Ecuaciones factorizadas
Las ecuaciones factorizadas son ecuaciones del tipo:
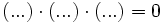
donde cada factor 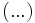 es una expresión algebraica.
es una expresión algebraica.
Como para que un producto sea cero basta con que uno de los factores sea cero, tenemos que igualar a cero cada factor y resolver la ecuación resultante.