Figuras semejantes. Escala (PACS)
De Wikipedia
| Revisión de 11:02 15 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:04 15 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| {{Figuras semejantes}} | {{Figuras semejantes}} | ||
| + | {{Semejanza de triángulos}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 11:04 15 ene 2009
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Figuras semejantes
- Dos figuras son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. Esto lo expresaremos matemáticamente diciendo que:
- Los segmentos correspondientes (homólogos) son proporcionales.
- Sus ángulos correspondientes (homólogos) son iguales.
- Al ser los segmentos homólogos proporcionales, se cumple que la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada razón de semejanza.
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Ejemplos: Figuras semejantes
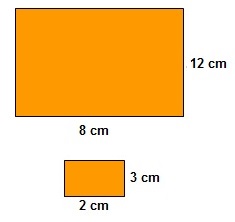
- Tenemos dibujado en un papel un rectángulo de dimensiones 12 cm x 8 cm. Hacemos una fotocopia reducida y obtenemos otro rectángulo de dimensiones 3 cm x 2 cm. Comprueba que son semejantes y calcula la razón de semejanza. Calcula el procentaje de reducción aplicado en la fotocopia.
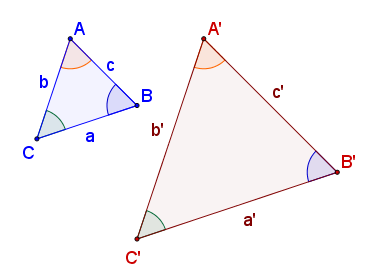
- Dos triángulos semejantes tienen una razón de semejanza de 0.75. Si los lados del mayor miden 12, 8 y 16 cm, respectivamente, ¿cuánto miden los lados del menor?
Solución 1:
Si dividimos las longitudes del rectángulo pequeño entre las correspondientes del grande, obtenemos: 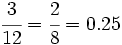 Por tanto la razón de semejanza es 0.25. Observa como los dos rectángulos tienen todos sus ángulos de 90º, es decir, la reducción no ha afectado a los ángulos.
La razón de semejanza puede expresarse en porcentaje: 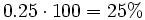 Por tanto la fotocopia es una reducción del 25%. |
| Solución 2:
Llamemos a, b y c, a los lados del triángulo menor, y a´, b´ y c´, a los del mayor. Sabemos que a´=12 cm, b´=8 cm y c´=16 cm. Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75: 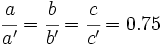 Entonces: |
Hola, les comparto este vídeo que es uno de mis favoritos y trata de las figuras semejantes, que son las figuras que tienen la misma forma, los mismos ángulos y distinto tamaño (lados proporcionales).
Actividades para que puedas aprender los concepto de semejanza y de razón de semejanza. También podrás aprender a construir figuras semejantes a una dada.
Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
- Los ángulos correspondientes son todos iguales.
- Los segmentos correspondientes son proporcionales.
En efecto,
1. Los ángulos son iguales ya que los lados correspondientes son paralelos.
2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza.
Mueve ahora el punto rojo para comprobar el valor de r.
Dibuja un cuadrado semejante a otro de lado 2 cm, con razón de semejanza 3.
María ha dibujado dos rectángulos. El primero tiene 4 cm de base y 7 cm de altura, y el segundo tiene 12 cm de base y 21 cm de altura. ¿Son semejantes? Calcula la razón de semejanza.
Determina si son semejantes dos rectángulos, el primero de base 7 cm y altura 2 cm, y el segundo de base 14 cm y altura 4 cm. Calcula la razón de semejanza.
Determina si son semejantes dos rectángulos, el primero de base 3 cm y altura 6 cm, y el segundo de base 6 cm y altura 10 cm.
Relación entre las áreas y los volúmenes de dos figuras semejantes
Propiedades
Si dos figuras son semejantes y k es la constante de proporcionalidad, entonces:
- La razón entre sus áreas es k2.
- La razón entre sus volúmenes k3.
Ejemplos: Relación entre las áreas y los volúmenes de dos figuras semejantes
- Comprueba que si un cuadrado tiene 5 cm de lado y el de otro cuadrado mide el doble, 10 cm, entonces el área de éste es el cuádruple de la del primero.
- Comprueba que si un cubo tiene 5 cm de arista y la de otro cubo mide el doble, 10 cm, entonces el volumen de éste es 8 veces la del primero.
Solución 1:
En efecto, como la razón entre los lados es 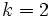 , la razón entre sus áreas es
, la razón entre sus áreas es 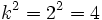 .
.
Si hallamos el área de cada cuadrado lo podremos comprobar:
- Área cuadrado pequeño=
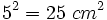
- Área cuadrado grande=
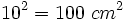
En efecto, el área del grande es el cuádruple del área del pequeño.
Solución 2:
En efecto, como la razón entre las aristas es 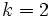 , la razón entre sus volúmenes es
, la razón entre sus volúmenes es 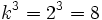 .
.
Si hallamos los volúmenes de cada cubo lo podremos comprobar:
- Volumen cubo pequeño=
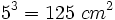
- Volumen cubo grande=
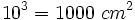
|
Ejercicio: Relación entre las áreas de dos figuras semejantes En una pizzería, la pizza pequeña tiene 23 cm de diámetro y es para una persona. Sin embargo, la pizza familiar tiene 46 cm de diámetro, justo el doble que la pequeña, pero dicen que es para 4 personas. ¿Nos están engañando? La respuesta en la siguiente actividad: |
Actividades en las que podrás ver la relación que existe entre las áreas de dos figuras semejantes.
Aprenderás a calcular la razón de semejanza de figuras semejantes conociendo los perímetros, las áreas (o superficies) y los volúmenes cuando se trate de cuerpos geométricos. Utilizo varios ejemplos y problemas para practicar lo explicado.
Un pintor pinta un boceto de un mural que ocupa 2 m2. Una vez acabado, el mural ha de ocupar una superficie de 50 m2. ¿Cuál es la razón de semejanza que hay entre el mural y el boceto?
La altura de un triángulo mide 10 cm y la base 6 cm. ¿Qué área tendrá un triángulo mayor semejante a éste con una razón de semejanza iguala a 4?
Dos hexágonos regulares tienen sus lados en proporción 1/3. El área del mayor es 117 cm<up>2</sup>. ¿Cuánto vale el área del menor?
Tenemos un cubo con un volumen de 32 cm3 y otro cubo con un volumen de 12 cm3. ¿Qué relación tienen las aristas y las superficies, respectivamente?
Un cono tiene una base de radio 3 cm y su altura es de 8 cm. Por otro lado, tenemos otro cono con un radio de la base de 6 cm y altura 16 cm. Indica si son semejantes ambos conos y, en tal caso, calcula la razón de semejanza y la razón entre sus volúmenes.
Una pelota de jugar a la petanca tiene un diámetro de 10 cm, y una pelota de ping-pong tiene un diámetro de 4 cm. Calcula la razón entre sus volúmenes.
Escala
Cuando representamos una casa en un plano, un coche en una maqueta o la superficie terrestre en un mapa, estamos representando figuras semejantes a las reales. La razón de semejanza entre dichas figuras diremos que es la escala del mapa, de la maqueta o del plano.
La escala es el cociente entre la longitud de un segmento en la reproducción y el correspondiente segmento en la realidad. Esto es, la escala es la razón de semejanza entre la reproducción y la realidad.
|
|
En este vídeo trabajamos con Escalas en Mapas y Planos. A través de varios ejercicios, aprenderás a hallar el valor real de medidas en planos y viceversa, el valor que debe tener en el plano una medida real.
Así, por ejemplo, decimos que un plano está a escala 1:100, si al realizar una medida de 1 cm en el plano, esta representa 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es 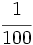 .
.
Tipos de escalas
Existen tres tipos de escalas:
- Escala natural: Cuando el tamaño del objeto representado en el plano coincide con la realidad. (1:1).
- Escala de reducción: Se utiliza cuando el tamaño del objeto en el plano es menor que la realidad. Esta escala se utiliza para representar piezas (1:2 ó 1:5), planos de viviendas (1:50), mapas físicos de territorios donde la reducción es mucho mayor (1:50.000 ó 1:100.000).
- Escala de ampliación: Se utiliza cuando hay que hacer el plano de piezas muy pequeñas o de detalles de un plano. En este caso el valor del numerador es más alto que el valor del denominador. Ejemplos: 2:1 ó 10:1.
Actividades para que puedas aprender a trabajar con escalas.
Ejercicios
Ejercicios resueltos sobre escalas.
En una fotografía, la imagen de un persona mide 12 cm, ¿qué escala se ha utilizado si la persona mide en realidad 1.80 m?.
Los planos de un juguete están a escala 1:10. ¿Cuál es la longitud del juguete si en el plano mide 8 cm?.
Queremos hacer una reproducción a escala 1:5 de un cuadro de 2 m de largo por 80 cm de ancho. Calcula las dimensiones de nuestra reproducción.
Si el volumen de un depósito es de 25 000 m3, ¿qué volumen tiene una maqueta hecha a escala 1:20?
Triángulos semejantes
Teorema de Tales
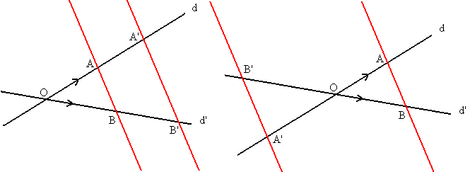
Teorema de Tales
Dos rectas d y d', que se cortan en un punto O, cortadas por rectas paralelas AB y A'B', determinan segmentos proporcionales:
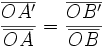 |
Triángulos en la posición de Tales
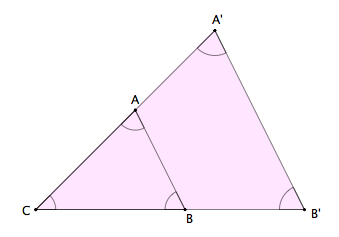
| Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales |
Triángulos en la posición de Tales
Dos triángulos son semejantes si y sólo si están en la posición de Tales.
Observa la siguiente escena y mueve el punto verde para desplazar el triángulo amarillo. Podrás comprobar que los ángulos son iguales
Criterios de semejanza de triángulos
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
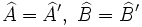
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
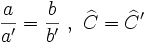
- Dos triángulos son semejantes si tienen los lados proporcionales:
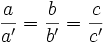
- En efecto, si tienen dos ángulos respectivamente iguales, el tercero también lo tienen igual. Entonces, esos dos triángulos se pueden poner en la posición de Tales y, en consecuencia, son semejantes.
Aplicaciones de los criterios de semejanza
|
Actividad Interactiva: Aplicaciones de los criterios de semejanza
Actividad 1: Cálculo de la altura conocida la sombra.
Actividad: La distancia del Sol a la Tierra es muy grande comparada con la tierra y con los objetos que hay sobre ella, de forma que podemos considerar que los rayos del Sol sobre objetos próximos son paralelos. En consecuencia, los triángulos que forma tienen sus ángulos iguales y, por tanto, son semejantes. Entonces, al ser los lados de los triángulos proporcionales, tenemos: 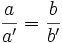 expresión de la cual, conocidos 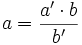
Actividad 2: Halla la altura de un árbol con la ayuda de un espejo y una cinta métrica.
Actividad: Los triángulos ABC y A'BC' son semejantes. ¿Por qué? En el punto B se coloca un espejo de forma que desde A se vea el extremo del árbol a través de él. Calcula la altura del árbol. Pon como distancia AC tu estatura y sitúa el punto C donde te parezca más conveniente. La altura calculada ¿depende de la altura del observador y de donde se sitúe?
Actividad 3: Semejanza en triángulos rectángulos.
Actividad: El triángulo ABC es rectángulo, y también lo son los triángulos ACM y BCM. Toma las medidas que necesites para comprobar que los dos triángulos coloreados son semejantes. También se puede comprobar que son semejantes si nos fijamos en sus ángulos. ¿Por qué? Además, cada uno de ellos de los dos triángulos es también semejante al triángulo ABC. ¿Por qué? |
Áreas y volúmenes de figuras semejantes
La relación entre el área A1, el volumen V1 de una figura F1, semejante a otra F2 de área A2 y volumen V2 y con razón de semejanza r es:
|
|
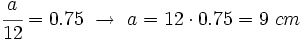
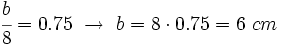
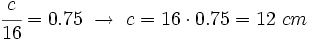
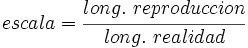 .
.
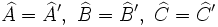
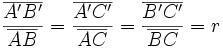
 , se la razón de semejanza.
, se la razón de semejanza.
 ,
,  y
y 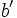 , podemos despejar
, podemos despejar 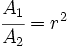 ;
;