Plantilla:Dominio e imagen de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:36 20 ene 2009 Coordinador (Discusión | contribuciones) (→Dominio de definición e imagen) ← Ir a diferencia anterior |
Revisión de 17:45 20 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Dominio de definición e imagen== | ==Dominio de definición e imagen== | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| - | |texto= Llamamos '''dominio de definición''' de una función <math>y=f(x)</math> al conjunto de valores de la variable independiente <math>x</math> para los cuales existe el valor de <math>y</math>. Lo representaremos por <math>D_f</math> .<br>La '''imagen''' o '''recorrido''' de una función es el conjunto de valores que toma la variable dependiente <math>y</math>. Lo representaremos por <math>Im_f</math> . | + | |texto= Llamamos '''dominio de definición''' de una función <math>y=f(x)\;</math> al conjunto de valores de la variable independiente <math>x\;</math> para los cuales existe el valor de <math>y\;</math>. Lo representaremos por <math>D_f\;</math> .<br>La '''imagen''' o '''recorrido''' de una función es el conjunto de valores que toma la variable dependiente <math>y\;</math>. Lo representaremos por <math>Im_f\;</math> . |
| }}{{p}} | }}{{p}} | ||
| {{AI2|titulo=Actividad Interactiva: ''Dominio e imagen''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Dominio e imagen''|cuerpo= | ||
Revisión de 17:45 20 ene 2009
Dominio de definición e imagen
Llamamos dominio de definición de una función  al conjunto de valores de la variable independiente
al conjunto de valores de la variable independiente  para los cuales existe el valor de
para los cuales existe el valor de  . Lo representaremos por
. Lo representaremos por 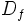 .
.
La imagen o recorrido de una función es el conjunto de valores que toma la variable dependiente  . Lo representaremos por
. Lo representaremos por 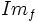 .
.
|
Actividad Interactiva: Dominio e imagen
1. Determina el dominio y la imagen de las siguientes funciones.
Actividad: Observa la escena y mueve el punto P para ver los valores que recorren las variables: a) Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X,¿Cuál es su dominio y su imagen? Observa esta otra escena y procedede como antes: b) ¿Cuál es su dominio y su imagen? Haz lo mismo con esta tercera escena: |
Ejemplo: Dominio de una función
- Halla el dominio de las funciones:
- a)
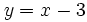 , b)
, b) 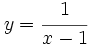 , c)
, c) 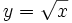
- a)
Solución:
- a) Su dominio es
 , porque cualquier valor de
, porque cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
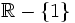 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
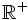 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
Ejercicios
|
Ejercicios: Dominio e imagen |

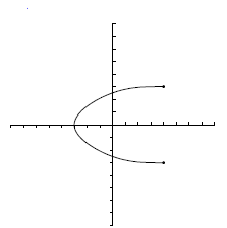
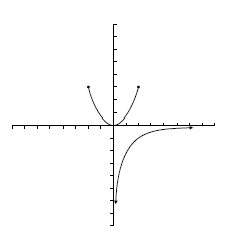
![D=[-3.5, 4]\;\!](/wikipedia/images/math/6/f/4/6f4030ef099e99944025cbb34e75c6ae.png) .
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
.

