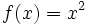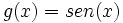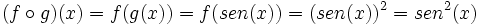Composición de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:15 23 ene 2009 Coordinador (Discusión | contribuciones) (→Función compuesta) ← Ir a diferencia anterior |
Revisión de 19:21 23 ene 2009 Coordinador (Discusión | contribuciones) (→Función compuesta) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| <center><math> | <center><math> | ||
| \begin{matrix} | \begin{matrix} | ||
| - | X & \to & \,\,Y\;\; & \to & Z | + | X & \to & \,\,\,Y\;\; & \to & Z \; |
| \\ | \\ | ||
| x & \to & f(x) & \to & g(f(x)) | x & \to & f(x) & \to & g(f(x)) | ||
Revisión de 19:21 23 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
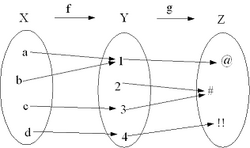
Función compuesta
| La función compuesta es una función formada por la aplicación sucesiva de otras dos funciones. Formalmente:
Dadas dos funciones 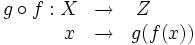 Se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. 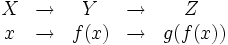 La expresión |
Ejemplo: Composición de funciones
Dadas las funciones
- a) Halla la función
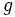 compuesta con
compuesta con  .
.
- b) Halla la función
 compuesta con
compuesta con 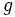 .
.
- a) Halla la función
Solución:
a) La función 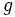 compuesta con
compuesta con  es:
es:
b) La función  compuesta con
compuesta con 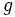 es:
es:
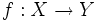 y
y 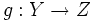 , donde la imagen de
, donde la imagen de 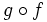 se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.