Plantilla:Dominio e imagen de una función
De Wikipedia
| Revisión de 19:06 1 feb 2009 Coordinador (Discusión | contribuciones) (→Dominio e imagen de una función) ← Ir a diferencia anterior |
Revisión de 19:10 1 feb 2009 Coordinador (Discusión | contribuciones) (→Dominio e imagen de una función) Ir a siguiente diferencia → |
||
| Línea 60: | Línea 60: | ||
| *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos) | *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos) | ||
| *Por voluntad de quien propone la función. | *Por voluntad de quien propone la función. | ||
| - | |||
| - | {{p}} | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''Dominio de una función'' | ||
| - | |enunciado= | ||
| - | :Halla el dominio de las funciones: | ||
| - | ::a) <math>y=x-3 \ , \quad x \in [-1,1]\;\!</math> | ||
| - | |||
| - | ::b) <math>y=\cfrac{1}{x-1}</math> | ||
| - | |||
| - | ::c) <math>y=\sqrt{x}</math> | ||
| - | |||
| - | ::d) <math>A=l^2\;</math> (Área de un cuadrado de lado <math>l\;</math>) | ||
| - | |sol= | ||
| - | :a) Su dominio es <math>[-1,1]\;\!</math>, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de <math>x\;</math> da un valor de <math>y\;</math> válido. | ||
| - | |||
| - | :b) Su dominio es <math>\mathbb{R}- \left \{ 1 \right \}</math>, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división. | ||
| - | |||
| - | :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | ||
| - | |||
| - | :d) Su dominio es <math>(0, + \infty)</math>, porque el lado de un cuadrado sólo puede tomar valores positivos | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| Línea 107: | Línea 85: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejemplo: ''Dominio de definición de una función'' | ||
| + | |enunciado= | ||
| + | :Halla el dominio de las funciones: | ||
| + | ::a) <math>y=x-3 \ , \quad x \in [-1,1]\;\!</math> | ||
| + | |||
| + | ::b) <math>y=\cfrac{1}{x-1}</math> | ||
| + | |||
| + | ::c) <math>y=\sqrt{x}</math> | ||
| + | ::d) <math>A=l^2\;</math> (Área de un cuadrado de lado <math>l\;</math>) | ||
| + | |sol= | ||
| + | :a) Su dominio es <math>[-1,1]\;\!</math>, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de <math>x\;</math> da un valor de <math>y\;</math> válido. | ||
| + | |||
| + | :b) Su dominio es <math>\mathbb{R}- \left \{ 1 \right \}</math>, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división. | ||
| + | |||
| + | :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | ||
| + | |||
| + | :d) Su dominio es <math>(0, + \infty)</math>, porque el lado de un cuadrado sólo puede tomar valores positivos | ||
| + | }} | ||
| + | {{p}} | ||
| {{ejemplo2 | {{ejemplo2 | ||
| |titulo=Ejemplos: ''Dominio de definición de una función'' | |titulo=Ejemplos: ''Dominio de definición de una función'' | ||
Revisión de 19:10 1 feb 2009
Dominio e imagen de una función
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 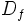 ó
ó 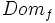
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
 . Lo representaremos por
. Lo representaremos por 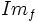 o
o 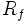 .
.
- Dominio de definición de una función.
- Interpretación gráfica del dominio.
- Necesidad de saber el dominio de una función.
- Ejemplos.
|
Actividad Interactiva: Dominio e imagen
1. Determina el dominio y la imagen de las siguientes funciones.
Actividad: a) Observa la escena y mueve el punto P para ver los valores que recorren las variables: Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X,¿Cuál es su dominio y su imagen? b) Observa esta otra escena y procedede como antes: ¿Cuál es su dominio y su imagen? c) Haz lo mismo con esta tercera escena: |
Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
(Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos)
- Por voluntad de quien propone la función.
- Hay ciertas reglas en matemáticas que no se pueden violar. Aquí las vamos a recordar.
- Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas.
- Ejemplos de algunas funciones "peligrosas" y de otras que no presentan ningún problema.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
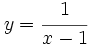
- b)
- c)
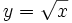
- c)
- d)
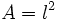 (Área de un cuadrado de lado
(Área de un cuadrado de lado 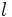 )
)
- d)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
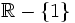 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
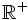 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
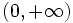 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Ejemplos: Dominio de definición de una función
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
|
Ejercicios: Dominio e imagen |

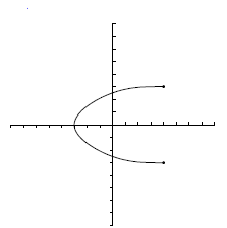
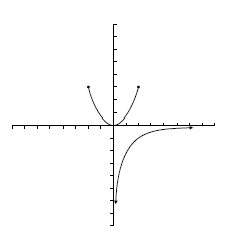
![D=[-3.5, 4]\;\!](/wikipedia/images/math/6/f/4/6f4030ef099e99944025cbb34e75c6ae.png) .
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
.

