Límite de una función en un punto (1ºBach)
De Wikipedia
| Revisión de 18:42 11 feb 2009 Coordinador (Discusión | contribuciones) (→Continuidad de una función en un punto) ← Ir a diferencia anterior |
Revisión de 18:46 11 feb 2009 Coordinador (Discusión | contribuciones) (→Discontinuidad evitable) Ir a siguiente diferencia → |
||
| Línea 129: | Línea 129: | ||
| |titulo1=Discontinuidad evitable | |titulo1=Discontinuidad evitable | ||
| |duracion=10'09" | |duracion=10'09" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=:Concepto de discontinuidad evitable. Ejemplos. |
| |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0303.html | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0303.html | ||
| }} | }} | ||
| Línea 150: | Línea 150: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Discontinuidad de primera especie=== | ===Discontinuidad de primera especie=== | ||
| {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> tiene una '''discontinuidad inevitable de salto finito''' (o de '''primera especie''') si existen los límites laterales, pero estos no coinciden | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> tiene una '''discontinuidad inevitable de salto finito''' (o de '''primera especie''') si existen los límites laterales, pero estos no coinciden | ||
Revisión de 18:46 11 feb 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
Aproximación a un punto
- Decimos que
 tiende a
tiende a  por la izquierda (
por la izquierda (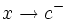 ) cuando a
) cuando a  se le dan valores menores que
se le dan valores menores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que
 tiende a
tiende a  por la derecha (
por la derecha (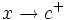 ) cuando a
) cuando a  se le dan valores mayores que
se le dan valores mayores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que
 tiende a
tiende a  (
( ) cuando a
) cuando a  se le dan valores cada vez más próximos a
se le dan valores cada vez más próximos a  .
.
- Los puntos en la recta real.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
- Concepto de distancia entre dos puntos.
- Concepto de entorno de un punto.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
Límite de de una función en un punto
Dada una función  , cuando la variable independiente
, cuando la variable independiente  se aproxima a un cierto punto
se aproxima a un cierto punto  , ya sea por la derecha o por la izquierda,
, ya sea por la derecha o por la izquierda,  va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
- Una función
 tiene límite por la izquierda en un punto
tiene límite por la izquierda en un punto  , si existe un número
, si existe un número 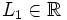 , de manera que cuando
, de manera que cuando 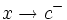 , los correspondientes valores
, los correspondientes valores 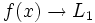 . Lo representaremos:
. Lo representaremos:
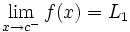
- Una función
 tiene límite por la derecha en un punto
tiene límite por la derecha en un punto  , si existe un número
, si existe un número 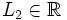 , de manera que cuando
, de manera que cuando 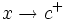 , los correspondientes valores
, los correspondientes valores 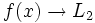 . Lo representaremos:
. Lo representaremos:
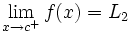
- Una función
 tiene límite en un punto
tiene límite en un punto  , si existe un número
, si existe un número 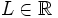 de manera que
de manera que
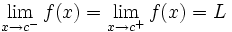
y lo representaremos:
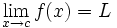
Nótese que aunque existan los límites laterales, si estos no coinciden, el límite no existe.
- Recordando el concepto de función.
- Conceptos de límite de una función por la derecha y por la izquierda de un punto.
- Concepto de límite de una función en un punto.
- Se puede calcular el límite en un punto independientemente de que el punto pertenezca o no al dominio de la función. Ejemplos.
Límites infinitos. Asíntotas verticales
El concepto de límite visto en el apartado anterior puede extenderese al caso en que, al aproximarnos al punto  , la función se aproxime a
, la función se aproxime a  ó
ó  .
.
- Una función
 tiende a
tiende a  por la izquierda de un punto
por la izquierda de un punto  , si
, si  se aproxima a valores positivos cada vez más grandes y no acotables, cuando
se aproxima a valores positivos cada vez más grandes y no acotables, cuando 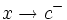 . Lo representaremos:
. Lo representaremos:
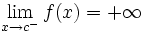
- Una función
 tiende a
tiende a  por la derecha de un punto
por la derecha de un punto  , si
, si  se aproxima a valores positivos cada vez más grandes y no acotables, cuando
se aproxima a valores positivos cada vez más grandes y no acotables, cuando 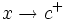 . Lo representaremos:
. Lo representaremos:
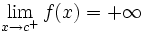
- Una función
 tiende a
tiende a  en un punto
en un punto  , si
, si

y lo representaremos:

- De forma análoga se puede definir la tendencia a
 si cambiamos la frase "se aproxima a valores positivos cada vez más grandes y no acotables" por "se aproxima a valores negativos cada vez más pequeños y no acotables", en los tres casos.
si cambiamos la frase "se aproxima a valores positivos cada vez más grandes y no acotables" por "se aproxima a valores negativos cada vez más pequeños y no acotables", en los tres casos.
- En todos estos casos diremos que la función tiene una asíntota vertical en el punto
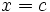 .
.
Continuidad de una función en un punto
Una función  es continua en un punto
es continua en un punto  , si se cumple que:
, si se cumple que:
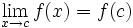
Para que ésto se cumpla deben ocurrir las tres condiciones siguientes:
- La función
 tiene límite en
tiene límite en 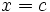 :
: 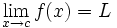
- La función está definida en
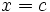 : Existe
: Existe 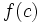
- Los dos valores anteriores coinciden:
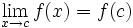
- Concepto de continuidad de una función en un punto. Ejemplo gráfico.
Tipos de discontinuidades
Discontinuidad evitable
Una función  tiene una discontinuidad evitable en un punto
tiene una discontinuidad evitable en un punto 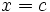 si existe
si existe 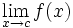 pero éste no coincide con
pero éste no coincide con 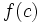 , bien porque
, bien porque  no esté definida en
no esté definida en 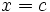 o bien porque simplemente sean distintos.
o bien porque simplemente sean distintos.
- Concepto de discontinuidad evitable. Ejemplos.
Ejemplos: Discontinuidad evitable
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Discontinuidad de primera especie
Una función  tiene una discontinuidad inevitable de salto finito (o de primera especie) si existen los límites laterales, pero estos no coinciden
tiene una discontinuidad inevitable de salto finito (o de primera especie) si existen los límites laterales, pero estos no coinciden
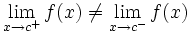
Video tutorial de matematicasbachiller.com
Ejemplos: Discontinuidad de primera especie
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Discontinuidad de segunda especie
Una función  tiene una discontinuidad inevitable de salto infinito (o de segunda especie) si no existe alguno de los límites laterales, bien porque este sea infinito o porque simplemente no exista.
tiene una discontinuidad inevitable de salto infinito (o de segunda especie) si no existe alguno de los límites laterales, bien porque este sea infinito o porque simplemente no exista.
Video tutorial de matematicasbachiller.com
Estudio de la continuidad de una función
Video tutorial de matematicasbachiller.com
Ejemplos: Criterios de continuidad
40 ejemplos del estudio de la continuidad de una función.
21 ejemplos del estudio de la continuidad de una función.
17 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com

