Plantilla:Aplicaciones del teorema de Pitágoras
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:17 15 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:59 16 feb 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 35: | Línea 35: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=3. Halla la altura de un triángulo equilatero de 4 cm. de lado. | + | |enunciado=3. El tamaño de las pantallas de televisión viene dado por la longitud en pulgadas de la diagonal de la pantalla (una pulgada equivale a 2,54 cm). Si un televisor mide 34,5 cm de base y 30 cm de altura, ¿cuál será su tamaño? |
| + | |actividad= | ||
| + | <center><iframe> | ||
| + | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411301056_PRE_0_1202237329&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); | ||
| + | width=530 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411301056_PRE_0_1202237329&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=4. Halla la altura de un triángulo equilatero de 4 cm. de lado. | ||
| |actividad= | |actividad= | ||
| Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir. | Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir. | ||
| Línea 49: | Línea 60: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=4. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm. | + | |enunciado=5. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm. |
| |actividad= | |actividad= | ||
| Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. | Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. | ||
| Línea 62: | Línea 73: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=5. Calcular el área de un cuadrado inscrito en una circunferencia de 3 cm de radio. | + | |enunciado=6. Calcular el área de un cuadrado inscrito en una circunferencia de 3 cm de radio. |
| |actividad= | |actividad= | ||
| Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir. | Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir. | ||
Revisión de 19:59 16 feb 2009
|
Actividades Interactivas: Aplicaciones del teorema de Pitágoras
1. Conocidos los catetos: a=4 cm. y b=5 cm., calcular la hipotenusa, c.
Actividad: Usaremos el teorema de Pitágoras: 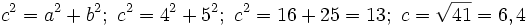 Compruébalo en la escena siguiente:
2. Conocido un cateto a=5 cm. y la hipotenusa c=8 cm., calcular el otro cateto, b.
Actividad: Usaremos, de nuevo, el teorema de Pitágoras: 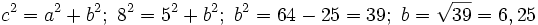 Compruébalo en la escena siguiente:
3. El tamaño de las pantallas de televisión viene dado por la longitud en pulgadas de la diagonal de la pantalla (una pulgada equivale a 2,54 cm). Si un televisor mide 34,5 cm de base y 30 cm de altura, ¿cuál será su tamaño?
4. Halla la altura de un triángulo equilatero de 4 cm. de lado.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir.
5. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura.
6. Calcular el área de un cuadrado inscrito en una circunferencia de 3 cm de radio.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir. |

