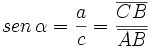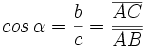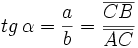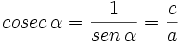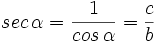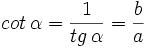Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 13:18 20 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:30 20 feb 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 38: | Línea 38: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos|contenido= | + | {{AI2|titulo=Actividad interactiva: ''Razaones trigonométricas''|cuerpo= |
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' Practica con las razones trigonométricas y ponte a prueba con una autoevaluación | ||
| + | |actividad={{p}} | ||
| + | *Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo. | ||
| + | *Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas. | ||
| + | *Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas. | ||
| + | *Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes. | ||
| <center><iframe> | <center><iframe> | ||
| url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html | ||
| Línea 47: | Línea 54: | ||
| <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Relaciones fundamentales de la trigonometría== | ||
| + | {{Teorema|titulo=Relaciones fundamentales de la trigonometría | ||
| + | |enunciado= | ||
| + | |demo= | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 13:30 20 feb 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Razones trigonométricas
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo  , de la siguiente manera: , de la siguiente manera:
|
Razones trigonométricas recíprocas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón recíproca del seno:
- La secante (abreviado como sec), razón recíproca del coseno:
- La cotangente (abreviado como cot), razón recíproca de la tangente:
|
Actividad interactiva: Razaones trigonométricas
Actividad 1: Practica con las razones trigonométricas y ponte a prueba con una autoevaluación
Actividad:
|