Razones trigonométricas de ángulos cualesquiera (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:49 1 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:01 20 feb 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Circunferencia goniométrica== | ||
| + | {{Tabla75|celda2=[[Imagen:goniometrica.png|300px]] | ||
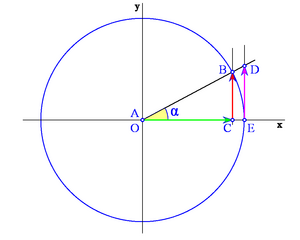
| + | |celda1=Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante. Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas '''O'''. Sobre ella situaremos nuestro triángulo rectángulo, haciendo coincidir su vértice '''A''' con '''O''', y el cateto contiguo al ángulo <math>\alpha \;</math> situado en el eje X positivo. tal y como se muestra en la figura. A esta circunferencia la llamaremos '''circunferencia goniométrica'''. | ||
| + | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| |titulo1=Círculo Goniométrico | |titulo1=Círculo Goniométrico | ||
Revisión de 18:01 20 feb 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Circunferencia goniométrica
Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante. Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas O. Sobre ella situaremos nuestro triángulo rectángulo, haciendo coincidir su vértice A con O, y el cateto contiguo al ángulo  situado en el eje X positivo. tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.
| 
|
Círculo Goniométrico (12'55") Sinopsis: - Razones trigonométricas de un ángulo. Fórmula fundamental.
- Circúlo goniométrico.
- Interpretación geométrica de las razones trigonométricas.
- Medida en grados y radianes.
- Tablas de las razones trigonométricas de los ángulos principales.
- Signo de las razones trigonométricas segun el cuadrante del ángulo.
