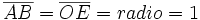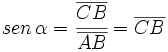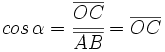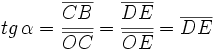Razones trigonométricas de ángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 19:11 20 feb 2009 Coordinador (Discusión | contribuciones) (→Circunferencia goniométrica) ← Ir a diferencia anterior |
Revisión de 19:12 20 feb 2009 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) Ir a siguiente diferencia → |
||
| Línea 40: | Línea 40: | ||
| Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo: | Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo: | ||
| - | {{Tabla50|celda1=<center>[[Imagen:goniometrica.png|280px]]</center>|celda2=<center>[[Imagen:goniometrica2.png|280px]]</center>}} | + | {{Tabla50|celda1=<center>[[Imagen:goniometrica.png|280px]]</center>|celda2=<center>[[Imagen:goniometrica2.jpg|280px]]</center>}} |
| - | {{Tabla50|celda1=<center>[[Imagen:goniometrica3.png|280px]]</center>|celda2=<center>[[Imagen:goniometrica4.png|280px]]</center>}} | + | {{Tabla50|celda1=<center>[[Imagen:goniometrica3.jpg|280px]]</center>|celda2=<center>[[Imagen:goniometrica4.jpg|280px]]</center>}} |
| {{Video_enlace2 | {{Video_enlace2 | ||
Revisión de 19:12 20 feb 2009
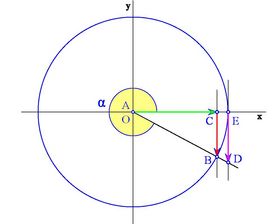
Circunferencia goniométrica
Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante.
Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas O. Sobre ella situaremos nuestro triángulo rectángulo ABC, haciendo coincidir su vértice A con O, el cateto contiguo al ángulo Teniendo en cuenta que | 
|
lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.
Razones trigonométricas de un ángulo cualquiera
Obsérvese como las coordenadas del punto B son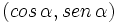 
. Y por extensión, podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
Dado un ángulo 
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte del segundo lado del ángulo con la circunferencia goniométrica:
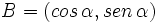
- Nota: Las relaciones fundamentales de la trigonometría, ya estudiadas anteriormente, siguen siendo válidas con esta definición.
Signo de las razones trigonométricas
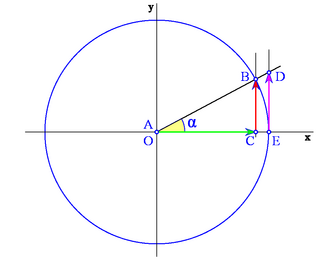
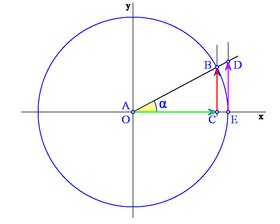
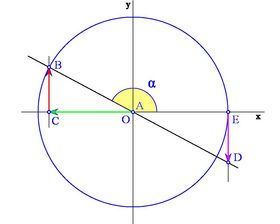
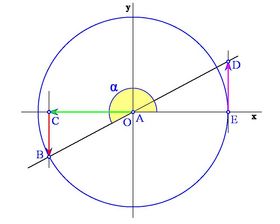
Según en qué cuadrante estemos, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, asignaremos signo positivo al coseno si está a la derecha de O y negativo si está a la izquierda.
Analogamente, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Asignaremos signo positivo al seno si está por encima y negativo si está por debajo.
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
|  |
 |  |
