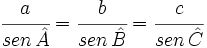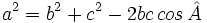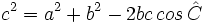Resolución de triángulos cualesquiera (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:51 22 feb 2009 Coordinador (Discusión | contribuciones) (→Teorema de los senos) ← Ir a diferencia anterior |
Revisión de 19:01 22 feb 2009 Coordinador (Discusión | contribuciones) (→Teorema del coseno) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| {{p}} | {{p}} | ||
| <center><math>a^2=b^2+c^2-2bc \, cos \, \hat A</math></center> | <center><math>a^2=b^2+c^2-2bc \, cos \, \hat A</math></center> | ||
| + | |||
| + | Y analogamente: | ||
| + | |||
| + | <center><math>b^2=a^2+c^2-2ac \, cos \, \hat B</math></center> | ||
| + | {{p}} | ||
| + | <center><math>c^2=a^2+b^2-2bc \, cos \, \hat C</math></center> | ||
| }} | }} | ||
| |demo= | |demo= | ||
Revisión de 19:01 22 feb 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Teorema de los senos
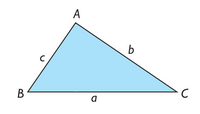
Teorema del coseno
Teorema del coseno
Demostración: