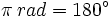Medida de ángulos: el radián (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:29 2 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:33 2 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==El radián== | ==El radián== | ||
| - | {{Caja_Amarilla|texto=El radián (simbolizado '''rad''') se define como el ángulo que limita un arco de circunferencia cuya longitud es igual a la del radio de la circunferencia.}} | + | {{Caja_Amarilla|texto=El '''radián''' (simbolizado '''rad''') se define como el ángulo que limita un arco de circunferencia cuya longitud es igual a la del radio de la circunferencia.}} |
| {{p}} | {{p}} | ||
| - | + | ==Equivalencia entre radianes y grados sexagesimales== | |
| - | + | {{Teorema | |
| + | |titulo=Equivalencia entre radianes y grados sexagesimales | ||
| + | |enunciado=:<math> \pi \, rad = 180^\circ</math> | ||
| + | |demo=Como la longitud de una circunferencia de radio <math>R \,</math> es <math>2 \pi R \,</math>, tenemos que una circunferencia contiene <math>2 \pi \,</math> veces a la radio. Por tanto, 360º equivalen a <math>2 \pi \,</math> rad y , dividiendo por 2, 180º equivalen a <math>\pi \,</math> rad. | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 18:33 2 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
El radián
El radián (simbolizado rad) se define como el ángulo que limita un arco de circunferencia cuya longitud es igual a la del radio de la circunferencia.
Equivalencia entre radianes y grados sexagesimales
Equivalencia entre radianes y grados sexagesimales
Demostración:
Como la longitud de una circunferencia de radio
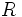es 
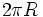, tenemos que una circunferencia contiene 
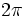veces a la radio. Por tanto, 360º equivalen a 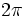rad y , dividiendo por 2, 180º equivalen a 
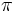rad.
