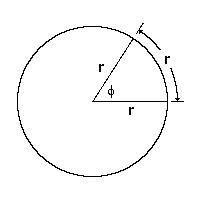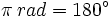Medida de ángulos: el radián (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:18 2 mar 2009 Coordinador (Discusión | contribuciones) (→Equivalencia entre radianes y grados sexagesimales) ← Ir a diferencia anterior |
Revisión de 19:21 2 mar 2009 Coordinador (Discusión | contribuciones) (→Equivalencia entre radianes y grados sexagesimales) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
| ==Equivalencia entre radianes y grados sexagesimales== | ==Equivalencia entre radianes y grados sexagesimales== | ||
| - | [[Imagen:Equivalradian.svg|300px|right]] | + | [[Imagen:Equivalradian.jpg|300px|right]] |
| {{Teorema | {{Teorema | ||
| |titulo=Equivalencia entre radianes y grados sexagesimales | |titulo=Equivalencia entre radianes y grados sexagesimales | ||
Revisión de 19:21 2 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
El radián
El radián (simbolizado rad) se define como el ángulo que abarca un arco de circunferencia cuya longitud es igual a la del radio de la circunferencia. En la figura adjunta el ángulo La utilidad de la medida en radianes frente a otras medidas de ángulos, es que ayuda a simplificar muchas fórmulas trigonométricas. | 
|
mide un radian porque abarca un arco que mide igual que el radio de la circunferencia.
Equivalencia entre radianes y grados sexagesimales
Equivalencia entre radianes y grados sexagesimales
|
|
Demostración:
Como la longitud de una circunferencia de radio
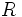es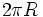 
, tenemos que una circunferencia contiene 
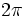veces a la radio. Por tanto, 360º equivalen a 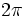rad y , dividiendo por 2, 180º equivalen a 
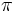rad.Utilizando la equivalencia anterior y mediante una regla de tres, podemos obtener las siguientes equivalencias:
| Grados | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
