Números complejos: Definición (1ºBach)
De Wikipedia
| Revisión de 19:14 4 mar 2009 Coordinador (Discusión | contribuciones) (→Opuesto y conjugado de un complejo) ← Ir a diferencia anterior |
Revisión de 19:23 4 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 43: | Línea 43: | ||
| ==El conjunto de los números complejos== | ==El conjunto de los números complejos== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Definimos el conjunto de los '''números complejos''' de la siguiente manera: | + | Definimos el conjunto<math>Escribe aquí una fórmula</math><math>Escribe aquí una fórmula</math> de los '''números complejos''' de la siguiente manera: |
| <center><math>\mathbb{C}=\big\{ a+bi \, / \, a, \, b \in \mathbb{R} \big\}</math></center> | <center><math>\mathbb{C}=\big\{ a+bi \, / \, a, \, b \in \mathbb{R} \big\}</math></center> | ||
| Línea 62: | Línea 62: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Representación gráfica de los números complejos== | ||
| + | Para representar los números reales utilizabamos una recta, la recta real. Para representar los números complejos vamos a utilizar un plano, el '''plano complejo'''. ¿Por qué?. Muy simple, un número complejo en forma binómica <math>a+bi\,</math> queda determinado por un par de números reales: su parte real, a\, y su parte imaginaria, <math>b\,</math>. De esta manera, el par <math>(a,b)\,</math> representa las coordenadas de un punto del plano. Diremos que <math>(a,b)\,</math> es el '''afijo''' del número complejo <math>a+bi\,</math>. | ||
| + | |||
| + | Ahora, al eje X, lo llamaremos '''eje real''' y al eje Y, '''eje imaginario'''. | ||
| + | |||
| + | También podemos representar al número complejo mediante un vector de origen <math>(0,0)\,</math> y extremo <math>(a,b)\,</math>. | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión de 19:23 4 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Necesidad de ampliación del campo numérico
Hay ecuaciones como
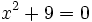
que no tienen solución en el conjunto de los números reales
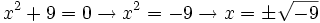 (no existe en
(no existe en  )
)Vamos a definir un nuevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Ese conjunto va a ser el conjunto de los números complejos. Para ello vamos a empezar dando sentido a las raíces de números negativos.
Unidad imaginaria
Se denomina unidad imaginaria a 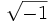 . Se designa por la letra
. Se designa por la letra 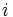
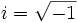
Con esta definición, la ecuación anterior ahora si tiene solución "imaginaria":
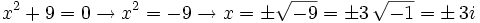
Potencias de la unidad imaginaria
A partir de 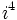 se repiten cíclicamente los valores.
se repiten cíclicamente los valores.
El conjunto de los números complejos
Definimos el conjuntoEscribeaquunafrmulaEscribeaquunafrmula de los números complejos de la siguiente manera:
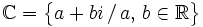
Forma binómica de un número complejo
- La expresión
 se denomina forma binómica de un número complejo. En ella, a
se denomina forma binómica de un número complejo. En ella, a  se le llama parte real y a
se le llama parte real y a  parte imaginaria.
parte imaginaria.
- Si
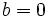 , lo que tenemos es un número real, por tanto
, lo que tenemos es un número real, por tanto 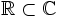 .
.
- Si
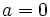 , se le llama número imaginario puro.
, se le llama número imaginario puro.
- Dos números complejos en forma binómica son iguales si tienen iguales sus partes reeales y sus partes imaginarias.
Opuesto y conjugado de un complejo
- Se define el opuesto de un complejo
 como el número complejo
como el número complejo 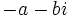 .
.
- Se define el conjugado de un complejo
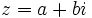 como el número complejo
como el número complejo 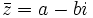 .
.
Representación gráfica de los números complejos
Para representar los números reales utilizabamos una recta, la recta real. Para representar los números complejos vamos a utilizar un plano, el plano complejo. ¿Por qué?. Muy simple, un número complejo en forma binómica  queda determinado por un par de números reales: su parte real, a\, y su parte imaginaria,
queda determinado por un par de números reales: su parte real, a\, y su parte imaginaria,  . De esta manera, el par
. De esta manera, el par 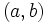 representa las coordenadas de un punto del plano. Diremos que
representa las coordenadas de un punto del plano. Diremos que 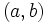 es el afijo del número complejo
es el afijo del número complejo  .
.
Ahora, al eje X, lo llamaremos eje real y al eje Y, eje imaginario.
También podemos representar al número complejo mediante un vector de origen 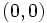 y extremo
y extremo 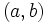 .
.
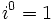
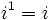
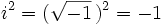
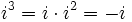
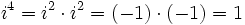
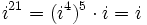 (Al hacer la división entera:
(Al hacer la división entera: 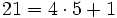 ).
).

