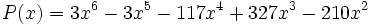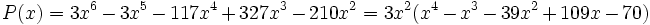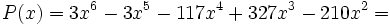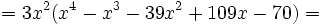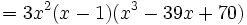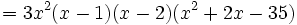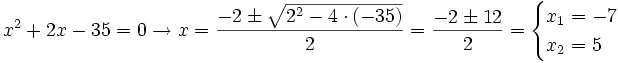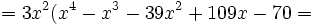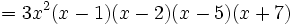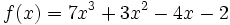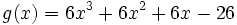Factorización de polinomios (1ºBach)
De Wikipedia
| Revisión de 17:16 13 ene 2009 Coordinador (Discusión | contribuciones) (→Procedimientos para la factorización de polinomios de grado mayor que 2) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Divisibilidad de polinomios== | + | {{Factorización de polinomios (1ºBach)}} |
| - | ===Polinomios múltiplos y divisores=== | + | |
| - | La divisibilidad en el conjunto de los polinomios es muy similar a la . | + | |
| - | {{p}} | + | |
| - | {{Caja_Amarilla|texto=Un polinomio <math>D(x)\,</math> es '''divisor''' de otro, <math>P(x)\,</math> y lo representaremos por <math>P(x)|Q(x)\;</math>, si la división <math>P(x):\,D(x)\,</math> es exacta. Es decir, cuando | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido=<math>P(x)=\,D(x)\cdot C(x)\,</math>}} | + | |
| - | {{p}} | + | |
| - | En tal caso, diremos que <math>P(x)\,</math> es '''divisible''' por <math>Q(x)\,</math>. También diremos que <math>P(x)\,</math> es un '''múltiplo''' de <math>D(x)\,</math>. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | <math>(3x+1) \cdot (x^2-5x+3) =3x^3-14x^2+4x+3 \Rightarrow (3x^3-14x^2+4x+3):(3x+1)=x^2-5x+3</math> | + | |
| - | }} | + | |
| - | La divisibilidad de polinomios es semejante a la [[Divisibilidad|divisibilidad con números enteros]]. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de '''máximo común divisor''', '''mínimo común múltiplo''' e '''irreducibilidad''' son similares a los correspondientes conceptos numéricos. | + | |
| - | {{p}} | + | |
| - | ===Polinomios irreducibles=== | + | |
| - | {{Caja_Amarilla|texto=Un polinomio <math>P(x)\,</math> es '''irreducible''' cuando ningún polinomio de grado inferior es divisor suyo.}} | + | |
| - | {{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | Son polinomios irreducibles, entre otros: | + | |
| - | * Los de primer grado: <math>3x,\ x-3,\ 5x-3\ \cdots \;</math> | + | |
| - | * Los de segundo grado sin raíces: <math>x^2+1,\ 2x^2-3x+5 \cdots \;</math> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | ==Factorización de polinomios== | + | |
| - | {{Caja_Amarilla|texto='''Factorizar''' un polinomio es descomponerlo en producto de polinomios con el menor grado posible.}} | + | |
| - | ===Factorización de polinomios de grado 2=== | + | |
| - | {{Teorema|titulo=''Factorización de polinomios de segundo grado'' | + | |
| - | |enunciado= | + | |
| - | Un polinomio de segundo grado, <math>kx^2+mx+n\;</math>, con raíces rales, <math>a\;</math> y <math>b\;</math>, se puede factorizar de la forma | + | |
| - | {{p}} | + | |
| - | <center><math>k(x-a)(x-b)\;</math></center> | + | |
| - | {{p}} | + | |
| - | |demo= | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{ejemplo|titulo=Ejemplos: ''Factorización de polinomios de segundo grado y reducibles'' | + | |
| - | |enunciado= Factoriza los siguientes polinomios | + | |
| - | ::a) <math>5x^2+5x-60\;</math> | + | |
| - | ::b) <math>5x^3+5x^2-60x\;</math> | + | |
| - | |sol= | + | |
| - | *El polinomio <math>5x^2+5x-60\;</math> tiene dos raíces: <math>x_1=3,\ x_2=-4</math>, que se obtienen de resolver la ecuación de segundo grado <math>5x^2+5x-60=0\;</math>. Entonces: | + | |
| - | {{p}} | + | |
| - | <center><math>5x^2+5x-60=5(x-3)(x+4)\;</math></center> | + | |
| - | {{p}} | + | |
| - | *El polinomio incompleto de grado 3, <math>5x^3+5x^2-60x\;</math>, se puede descomponer de la siguiente manera: | + | |
| - | {{p}} | + | |
| - | <center><math>5x^3+5x^2-60x=x(5x^2+5x-60)=5x(x-3)(x+4)\;</math></center> | + | |
| - | {{p}} | + | |
| - | :(Observa que primero hemos sacado factor común <math>x\;</math> y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior). | + | |
| - | }} | + | |
| - | ===Procedimientos para la factorización de polinomios de grado mayor que 2=== | ||
| - | {{caja_Amarilla|texto= | ||
| - | *Siempre que se pueda, sacaremos <math>x\;</math> '''factor común'''. | ||
| - | *Mediante la '''[[Cociente de Polinomios. Regla de Ruffini (4ºESO-B)#División de un polinomio por (x-a). Regla de Ruffini|regla de Ruffini]]''' buscaremos las '''[[Factorización de Polinomios (4ºESO-B)#Raíces enteras de un polinomio|raíces enteras del polinomio]]''', que se hallan entre los divisores del término independiente. Así, si encontramos una raíz <math>x=a\;</math> de un polinomio <math>P(x)\;</math>, tendremos que <math>P(x)=(x-a)Q(x)\;</math>, donde <math>Q(x)\;</math> tiene un grado menos que <math>P(x)\;</math>. ([[Factorización de Polinomios (4ºESO-B)#Raíces de un polinomio|Ver raíces de un polinomio]]). | ||
| - | }} | ||
| - | Un polinomio de grado mayor que 2 no pueda factorizarse usando los procedimientos anteriores, es poco probable que podamos hacerlo con los conocimientos que tenemos. | ||
| - | |||
| - | En algunos casos, como en el de los '''polinomios bicuadrados''', que son polinomios de la forma <math>ax^4+bx^2+c\;</math>, si podremos hallarle las raices, resolviendo la [[Otros Tipos de Ecuaciones (4ºESO-B)#ecuaciones bicuadradas|ecuación bicuadrada]] que resulta de igualarlo a cero. | ||
| - | {{p}} | ||
| - | {{ejemplo|titulo=Ejemplos: ''Factorización de polinomios bicuadrados'' | ||
| - | |enunciado= Factoriza el siguiente polinomio: <math>P(x)=x^4 - 7x^2 + 6 \;\!</math> | ||
| - | |sol= | ||
| - | Resolvemos la ecuación bicuadrada: <math>x^4 - 7x^2 + 6 = 0\;\!</math> | ||
| - | |||
| - | <math>x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6=0</math> | ||
| - | |||
| - | <math>y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}</math> | ||
| - | |||
| - | '''Soluciones:''' <math>-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!</math> | ||
| - | |||
| - | Entonces, la factorización del polinomio es la siguiente: | ||
| - | |||
| - | <center><math>P(x)=(x+1)(x-1)(x+\sqrt 6)(x-\sqrt 6)</math></center> | ||
| - | }} | ||
| - | |||
| - | ===Factorización de un polinomio mediante la regla de Ruffini=== | ||
| - | Para factorizar un polinomio mediante la [[Cociente de Polinomios. Regla de Ruffini (4ºESO-B)#División de un polinomio por (x-a). Regla de Ruffini|regla de Ruffini]], aplicaremos ésta sucesivamente, utilizando como candidatos a raíces los divisores del término independiente, hasta que nos quede un polinomio de segundo grado. Cuando estemos en este punto, aplicaremos la fórmula de la ecuación de segundo grado y obtendremos las dos últimas raíces y por tanto los dos últimos factores. Esto será así, siempre y cuando, el discriminante de la ecuación no sea negativo, ya que de serlo, no habrá más raíces y no podremos descomponerlo más. | ||
| - | |||
| - | <div style="background: white; padding:.75em; border:2px solid MediumBlue;border-left:4px solid MediumBlue;border-bottom:4px solid MediumBlue;"> | ||
| - | [[Image:ejemplo_blue.png|44px|left|ejercicio]] | ||
| - | <font color="MediumBlue">'''Ejemplo: ''Factorización de polinomios'''''</font> | ||
| - | ---- | ||
| - | Factoriza el siguiente polinomio: | ||
| - | ::<math>P(x)=3x^6-3x^5-117x^4+327x^3-210x^2\,\!</math> | ||
| - | <div class="NavFrame" style="background: white; border: 0px solid #aaaaaa; padding:3px; margin-bottom:0em; margin-left:0em;"> | ||
| - | <div class="NavHead rad" align="right" style="background: WhiteSmoke;">''Solución:''</div><div class="NavContent" align="left"> | ||
| - | ---- | ||
| - | Primero sacamos factor común <math>3x^2\,\!</math>: | ||
| - | :<math>P(x)=3x^6-3x^5-117x^4+327x^3-210x^2 = 3x^2 (x^4-x^3-39x^2+109x-70)\,\!</math> | ||
| - | |||
| - | Ahora aplicamos Ruffini. Los divisores de <math>70\,\!</math> son <math>1,\ -1,\ 2,\ -2,\ 5,\ -5,\ \mbox{etc.}\,\!</math> | ||
| - | |||
| - | Empezaremos probando con el <math>1\,\!</math> | ||
| - | |||
| - | :{| | ||
| - | |- style="height:50px" | ||
| - | | | ||
| - | |align="center" style="width:25px; border-left:1px solid black"|1 | ||
| - | |align="center" style="width:25px"| -1 | ||
| - | |align="center" style="width:25px"| -39 | ||
| - | |align="center" style="width:25px"|109 | ||
| - | |align="center" style="width:25px"| -70 | ||
| - | |- | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"| | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-bottom:1px solid black"|0 | ||
| - | |align="center" style="border-bottom:1px solid black"|-39 | ||
| - | |align="center" style="border-bottom:1px solid black"|70 | ||
| - | |- | ||
| - | | | ||
| - | |align="center" style="border-left:1px solid black"|1 | ||
| - | |align="center"|0 | ||
| - | |align="center"|-39 | ||
| - | |align="center"|70 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"|0 | ||
| - | |} | ||
| - | |||
| - | Como el resto es cero, hemos encontrado una de las raíces, x=1 y uno de los factores (x-1). | ||
| - | |||
| - | :<math>P(x)=3x^6-3x^5-117x^4+327x^3-210x^2 =\,\!</math> | ||
| - | :::<math>= 3x^2 (x^4-x^3-39x^2+109x-70=\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x^3 -39x +70)\,\!</math> | ||
| - | |||
| - | Seguimos aplicando Ruffini. Probamos con 1, de nuevo ya que podría repetirse dicha raíz: | ||
| - | |||
| - | :{| | ||
| - | |- style="height:50px" | ||
| - | | | ||
| - | |align="center" style="width:25px; border-left:1px solid black"|1 | ||
| - | |align="center" style="width:25px"| 0 | ||
| - | |align="center" style="width:25px"| -39 | ||
| - | |align="center" style="width:25px"|70 | ||
| - | |- | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"| | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-bottom:1px solid black"|-38 | ||
| - | |- | ||
| - | | | ||
| - | |align="center" style="border-left:1px solid black"|1 | ||
| - | |align="center"|1 | ||
| - | |align="center"|-38 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"|32 | ||
| - | |} | ||
| - | |||
| - | El resto es diferente de cero con lo que tenemos que seguir probando, con el -1: | ||
| - | :{| | ||
| - | |- style="height:50px" | ||
| - | | | ||
| - | |align="center" style="width:25px; border-left:1px solid black"|1 | ||
| - | |align="center" style="width:25px"| 0 | ||
| - | |align="center" style="width:25px"| -39 | ||
| - | |align="center" style="width:25px"|70 | ||
| - | |- | ||
| - | |align="center" style="border-bottom:1px solid black"|-1 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"| | ||
| - | |align="center" style="border-bottom:1px solid black"|-1 | ||
| - | |align="center" style="border-bottom:1px solid black"|1 | ||
| - | |align="center" style="border-bottom:1px solid black"|38 | ||
| - | |- | ||
| - | | | ||
| - | |align="center" style="border-left:1px solid black"|1 | ||
| - | |align="center"|-1 | ||
| - | |align="center"|-38 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"|108 | ||
| - | |} | ||
| - | |||
| - | El resto vuelve a ser diferente de cero, probamos con 2: | ||
| - | |||
| - | :{| | ||
| - | |- style="height:50px" | ||
| - | | | ||
| - | |align="center" style="width:25px; border-left:1px solid black"|1 | ||
| - | |align="center" style="width:25px"| 0 | ||
| - | |align="center" style="width:25px"| -39 | ||
| - | |align="center" style="width:25px"|70 | ||
| - | |- | ||
| - | |align="center" style="border-bottom:1px solid black"|2 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"| | ||
| - | |align="center" style="border-bottom:1px solid black"|2 | ||
| - | |align="center" style="border-bottom:1px solid black"|4 | ||
| - | |align="center" style="border-bottom:1px solid black"|70 | ||
| - | |- | ||
| - | | | ||
| - | |align="center" style="border-left:1px solid black"|1 | ||
| - | |align="center"|2 | ||
| - | |align="center"|-35 | ||
| - | |align="center" style="border-left:1px solid black; border-bottom:1px solid black"|0 | ||
| - | |} | ||
| - | |||
| - | Ya hemos encontrado otra raíz, x=2, y el factor correspondieente, (x-2). | ||
| - | |||
| - | El polinomio quedará de la siguiente forma: | ||
| - | |||
| - | :<math>P(x)=3x^6-3x^5-117x^4+327x^3-210x^2 =\,\!</math> | ||
| - | :::<math>= 3x^2 (x^4-x^3-39x^2+109x-70=\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x^3 -39x +70)\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x-2)(x^2+2x-35)\,\!</math> | ||
| - | |||
| - | Finalmente para encontrar las dos últimas raíces utilizamos la fórmula de la ecuación de 2º grado: | ||
| - | |||
| - | :<math>x^2+2x-35=0 \rightarrow x=\frac{-2 \pm \sqrt{2^2 -4 \cdot (-35)}}{2}=\frac{-2 \pm 12}{2}=\begin{cases} x_1=-7 \\ x_2=5 \end{cases}</math> | ||
| - | |||
| - | Así, sus raíces son 5 y -7 y sus factores (x-5) y (x+7). | ||
| - | |||
| - | De esta manera: | ||
| - | |||
| - | :<math>P(x)=3x^6-3x^5-117x^4+327x^3-210x^2 =\,\!</math> | ||
| - | :::<math>= 3x^2 (x^4-x^3-39x^2+109x-70=\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x^3 -39x +70)\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x-2)(x^2+2x-35)\,\!</math> | ||
| - | :::<math>= 3x^2(x-1)(x-2)(x-5)(x+7)\,\!</math> | ||
| - | |||
| - | Con lo que queda descompuesto el polinomio. | ||
| - | |||
| - | </div> | ||
| - | </div> | ||
| - | </div> | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Divisibilidad de polinomios
(pág. 74)
Polinomios múltiplos y divisores
- Un polinomio
 es divisor de otro,
es divisor de otro,  y lo representaremos por
y lo representaremos por 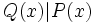 , si la división
, si la división 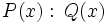 es exacta, es decir, cuando existe otro polinomio
es exacta, es decir, cuando existe otro polinomio 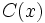 tal que
tal que 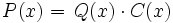 .
.
- En tal caso, diremos que
 es divisible por
es divisible por  y que
y que  es un múltiplo de
es un múltiplo de  .
.
- También diremos que
 y
y 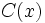 son factores del polnomio
son factores del polnomio  .
.
Dados los polinomios:
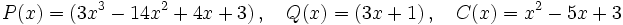 :
:Se cumple que
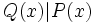 , porque
, porque 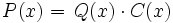 .
.Es decir, la siguiente división es exacta:
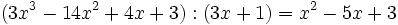
porque:
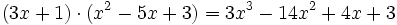
La divisibilidad de polinomios es semejante a la divisibilidad con números enteros. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de máximo común divisor, mínimo común múltiplo e irreducibilidad son similares a los correspondientes conceptos numéricos.
Polinomios irreducibles
Un polinomio  es irreducible cuando ningún polinomio de grado inferior (distinto de grado cero) es divisor suyo.
es irreducible cuando ningún polinomio de grado inferior (distinto de grado cero) es divisor suyo.
Son polinomios irreducibles, entre otros:
- Los de primer grado:
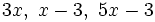
- Los de segundo grado sin raíces:
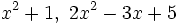
Máximo común divisor y mínimo común múltiplo
Se dice que el polinomio 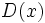 es el máximo común divisor de los polinomios
es el máximo común divisor de los polinomios  y
y  , y lo expresaremos:
, y lo expresaremos:
![m.c.d \,[P(x), Q(x)]=D(x)\;](/wikipedia/images/math/c/6/6/c66f3168e53561a04ed46aade0f24ca0.png)
si 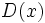 es divisor de ambos y no existe otro polinomio que divida a ambos que tenga mayor grado que él.
es divisor de ambos y no existe otro polinomio que divida a ambos que tenga mayor grado que él.
Se dice que el polinomio 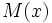 es el mínimo común múltiplo de los polinomios
es el mínimo común múltiplo de los polinomios  y
y  , y lo expresaremos:
, y lo expresaremos:
![m.c.m \,[P(x), Q(x)]=M(x)\;](/wikipedia/images/math/2/2/1/221e514439439421dc1201091dd735b3.png)
si 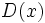 es múltiplo de ambos y no existe otro polinomio que sea múltiplo de ambos que tenga menor grado que él.
es múltiplo de ambos y no existe otro polinomio que sea múltiplo de ambos que tenga menor grado que él.
Raíces de un polinomio
Un número  es una raíz o un cero de un polinomio
es una raíz o un cero de un polinomio  , si
, si 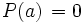 .
.
Dicho de otra forma, las raíces de un polinomio son las soluciones de la ecuación 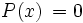 .
.
Raíces de un polinomio. Ejemplos.
Teorema del factor
 es una raíz de un polinomio
es una raíz de un polinomio  si y solo si
si y solo si 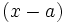 es un factor de dicho polinomio.
es un factor de dicho polinomio.
En efecto, si  es una raíz de
es una raíz de  , entonces
, entonces 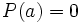 y, por el teorema del resto, el resto de dividir
y, por el teorema del resto, el resto de dividir  entre
entre 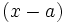 es cero. Así
es cero. Así 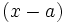 es un factor de
es un factor de  .
.
Factorización de polinomios
Factorizar un polinomio es descomponerlo como producto de otros polinomios con menor grado que el de partida.
Normalmente buscaremos la factorización máxima, que es la que se obtiene cuando los polinomios de la descomposición son irreducibles.
Por el teorema del factor, encontrar las raíces del polinomio nos ayudará a factorizarlo.
Factorización de polinomios:
- Extraer factores comunes.
- Utilizar las igualdades notables.
- Propiedad de factorización de los polinomios de 2º grado.
Introducción a la factorización de polinomios: Qué son los factores de un polinomio.
Introducción a la factorización de polinomios: Obtención de un polinomio a partir de sus raíces.
Introducción a la factorización de polinomios: Factorización de polinomios de grado 2.
Introducción a la divisibilidad y factorización de polinomios.
Ejemplos de distintas técnicas de factorización de polinomios.
Ejemplos de distintas técnicas de factorización de polinomios.
Factorización de monomios:
Elige la factorización correcta del monomio 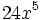 .
.
Encuentra el monomio que falta: 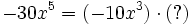 .
.
Encuentra el ancho de un rectángulo de área 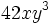 , uno de cuyos lados mide
, uno de cuyos lados mide 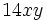 .
.
Determina el máximo común divisor de 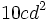 y
y 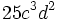 .
.
Actividad sobre divisibilidad y factorización de polinomios.
Factoriza monomios.
Máximo común divisor de monomios.
Divisibilidad y factorización de polinomios.
Factoriza monomios.
Distintas estrategias para la factorización de polinomios:
Factorizar expresiones cuadráticas en cualquier forma.
Factorización sacando factor común
Si quieres recordar cómo se saca factor común, a continuación tienes el enlace:
Factorización usando productos notables
Si quieres recordar las identidades notables y cómo se factoriza usando dichas identidades, aquí tienes el enlace:
Factorización de polinomios de grado 2
Factorización de polinomios de segundo grado
Un polinomio de segundo grado, 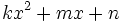 , con raíces rales,
, con raíces rales,  y
y  , se puede factorizar de la forma
, se puede factorizar de la forma
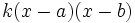
Ejemplos: Factorización de polinomios de segundo grado y reducibles
Factoriza los siguientes polinomios
- a)
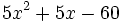
- b)
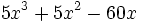
- El polinomio
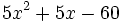 tiene dos raíces:
tiene dos raíces: 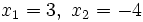 , que se obtienen de resolver la ecuación de segundo grado
, que se obtienen de resolver la ecuación de segundo grado 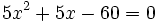 . Entonces:
. Entonces:
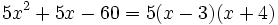
- El polinomio incompleto de grado 3,
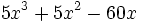 , se puede descomponer de la siguiente manera:
, se puede descomponer de la siguiente manera:
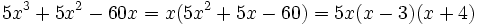
- (Observa que primero hemos sacado factor común
 y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
Descomposición factorial de polinomios de grado 2 resolviendo la ecuación de segundo grado.
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5a)
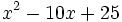
- 5b)
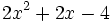
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5c)
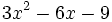
- 5d)
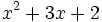
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5e)
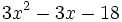
- 5f)
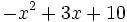
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- a)
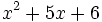
- b)
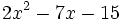
- c)
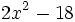
- d)
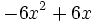
|
Actividad: Factorización de polinomios de grado 2 Factoriza los siguientes polinomios de grado 2 o reducibles a grado 2:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) factor 4x^2+4x+1 b) factor x^2+x+1 c) factor x^2-16x d) factor 4x^2-25 e) factor 5x^2+20 f) factor 4x^4+x^2 |
Procedimientos para la factorización de polinomios de grado mayor que 2
(pág. 75)
Procedimiento para factorizar polinomios
- Siempre que se pueda, sacaremos
 factor común.
factor común.
- Mediante la regla de Ruffini podremos buscar las raíces enteras o fraccionarias del polinomio y obtener la factorización.
Un polinomio de grado mayor que 2 no pueda factorizarse usando los procedimientos anteriores, es poco probable que podamos hacerlo con los conocimientos que tenemos.
En algunos casos, como en el de los polinomios bicuadrados, si podremos hallarle las raices, resolviendo la ecuación bicuadrada que resulta de igualarlo a cero.
Ejemplos: Factorización de polinomios bicuadrados
Factoriza el siguiente polinomio: 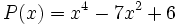
Resolvemos la ecuación bicuadrada: 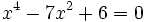
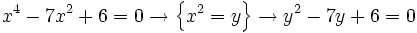
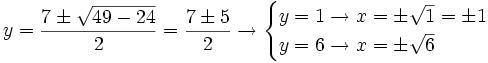
Soluciones: 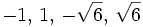
Entonces, la factorización del polinomio es la siguiente:
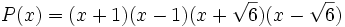
Factoriza los siguientes polinomios:
- 4a)
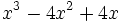
- 4b)
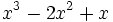
- 4c)
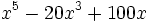
Factoriza los siguientes polinomios:
- 4d)
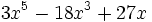
- 4e)
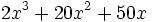
- 4f)
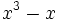
Factoriza los siguientes polinomios:
- 4g)
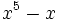
- 4h)
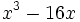
- 4i)
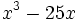
- 4j)
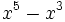
Factoriza los siguientes polinomios:
- 6a)
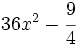
- 6b)
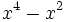
- 6c)
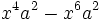
Factoriza los siguientes polinomios:
- 6d)

- 6e)
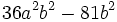
- 6f)
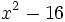
Factoriza los siguientes polinomios:
- 6g)
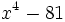
- 6h)

- 6i)
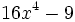
- 6j)
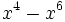
Factoriza los siguientes polinomios:
- 7a)
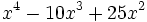
- 7b)

Factoriza los siguientes polinomios:
- 7c)
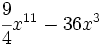
- 7d)
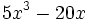
Factoriza los siguientes polinomios:
- 7e)
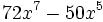
- 7f)
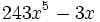
|
Actividad: Factorización de polinomios bicuadrados a) Factoriza el polinomio b) Halla las raíces del polinomio Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) factor x^4-5x^2+4 b) roots x^4-1 o bien solve x^4-1=0 over the reals. Y para factorizarlo: factor x^4-1=0 as real |
Factorización de un polinomio mediante la regla de Ruffini
Factorización de un polinomio por Ruffini
Para factorizar un polinomio mediante la regla de Ruffini, aplicaremos ésta sucesivamente, utilizando como candidatos a raíces enteras, los divisores del término independiente y como candidatos a raices fraccionarias, las que resultan de dividir los divisores del término independiente entre los divisores del término de mayor grado.
Cuando al aplicar la regla de Ruffini nos quede un polinomio de segundo grado en el cociente, en vez de seguir probando por Ruffini, es preferible aplicar la fórmula de la ecuación de segundo grado para obtener las dos últimas raíces y por tanto los dos últimos factores. Esto será así, siempre y cuando, el discriminante de la ecuación no sea negativo, ya que de serlo, no habrá más raíces y no podremos descomponerlo más.
Ejemplo: Regla de Ruffini
Factoriza el siguiente polinomio:
Primero sacamos factor común 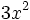 :
:
Ahora aplicamos Ruffini. Los divisores de 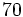 son
son 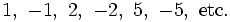
Empezaremos probando con el 1:
| 1 -1 -39 109 -70
|
1| 1 0 -39 70
--|----------------------
| 1 0 -39 70 |0
|____
Como el resto es cero, hemos encontrado una de las raíces, 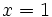 y uno de los factores
y uno de los factores 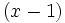 .
.
Seguimos aplicando Ruffini. Probamos con 1, de nuevo ya que podría repetirse dicha raíz:
| 1 0 -39 70
|
1| 1 1 38
--|-----------------
| 1 1 38 |108
|____
El resto es diferente de cero con lo que tenemos que seguir probando, con el -1:
| 1 0 -39 70
|
-1| -1 1 38
--|-----------------
| 1 -1 -38 |108
|____
El resto vuelve a ser diferente de cero, probamos con 2:
| 1 0 -39 70
|
2| 2 4 -70
--|----------------
| 1 2 -35 |0
|____
Ya hemos encontrado otra raíz,  , y el factor correspondiente,
, y el factor correspondiente, 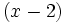 .
.
El polinomio quedará de la siguiente forma:
Finalmente para encontrar las dos últimas raíces utilizamos la fórmula de la ecuación de 2º grado:
Así, sus raíces son 5 y -7 y sus factores (x-5) y (x+7).
De esta manera:
Método que nos permite factorizar polinomios de grado mayor que dos.
- Factorizar un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil.
- Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x).
- Teorema de la factorización: si los coeficientes de un polinomio P(x) son números enteros, los ceros enteros de P(x) son divisores del término independiente de P(x).
- Si la suma de los coeficientes de P(x) es 0, pues apostar tranquilamente la vida a que el número 1 es un "cero" de P(x); o sea, P(x) es divisible por (x-1).
Cómo hacer una descomposición factorial de polinomios por Ruffini.
Factoriza los polinomios:
- a)
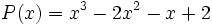
- b)
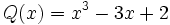
Factoriza el polinomio 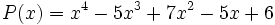
Factoriza el polinomio 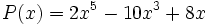
Factoriza el polinomio 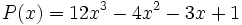 sabiendo que sólo tiene raíces fraccionarias.
sabiendo que sólo tiene raíces fraccionarias.
Hallar los puntos de intersección de las dos funciones polinómicas siguientes:
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8a)
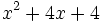
- 8b)
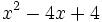
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8c)
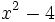
- 8d)
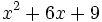
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8e)
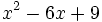
- 8f)
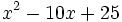
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8g)
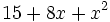
- 8h)
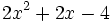
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8i)
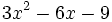
- 8j)
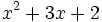
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8k)
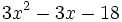
- 8l)
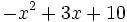
Ejercicios propuestos
|
Ejercicios propuestos: Factorización de polinomios |
Ejercicios y videotutoriales
Ejercicios resueltos sobre factorización de polinomios.
Ejercicios de autoevaluación sobre raíces de polinomios.
Ejercicios de autoevaluación sobre factorización de polinomios.
Ejercicios 9a-c: Factorizar polinomios:
- 9a)
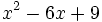
- 9b)
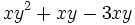
- 9c)
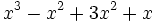
Ejercicios 9d-e: Factorizar polinomios:
- 9c)
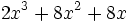
- 9d)
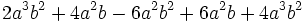
Factorizar polinomios:
- a)
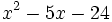
- b)
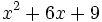
- c)
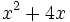
- d)
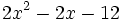
- e)
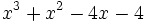
- f)
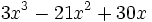
- g)
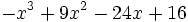
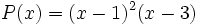
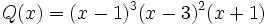 :
:
![m.c.d \,[P(x), Q(x)]=(x-1)^2(x-3)\;](/wikipedia/images/math/9/6/c/96c02ce39375f7c1585c25c27c0c0fcb.png)
![m.c.m \,[P(x), Q(x)]=(x-1)^3 (x-3)^2 (x+1)\;](/wikipedia/images/math/8/d/5/8d598eb8a1613c40ffc2eebba001fa1f.png)
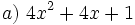
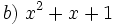
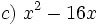
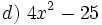
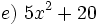
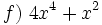
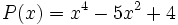
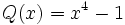 y factorízalo.
y factorízalo.