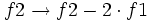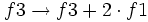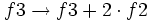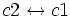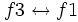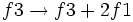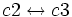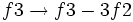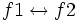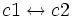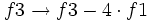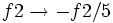Método de Gauss para sistemas lineales (1ºBach)
De Wikipedia
| Revisión de 15:17 8 ene 2009 Coordinador (Discusión | contribuciones) (→Discusión de sistemas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| __TOC__ | __TOC__ | ||
| - | ==Método reducción de Gauss== | + | {{Método de Gauss (1ºBACH)}} |
| - | {{Caja_Amarilla|texto= | + | |
| - | El '''método de Gauss''' que se debe al matemático alemán [[Gauss|Johann Carl Friedrich Gauss]], es una generalización del método de reducción, que utilizamos para eliminar una incógnita en los sistemas de dos ecuaciones con dos incógnitas. Consiste en la aplicación sucesiva del método de reducción, utilizando los criterios de equivalencia de sistemas, para transformar el sistema de ecuaciones en un sistema escalonado.}} | + | |
| - | {{p}} | + | |
| - | Las '''operaciones''' que podemos realizar sobre las ecuaciones del sistema inicial para transformarlo en otro equivalente, son las siguientes: | + | |
| - | *Multiplicar o dividir una ecuación por un número real distinto de cero. | ||
| - | *Sumarle o restarle a una ecuación otra ecuación. | ||
| - | *Sumarle a una ecuación otra ecuación multiplicada por un número distinto de cero. | ||
| - | *Cambiar el orden de las ecuaciones. | ||
| - | *Cambiar el orden de las incógnitas del sistema. | ||
| - | *Eliminar ecuaciones nulas (0=0). | ||
| - | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Método de reducción de Gauss'' | ||
| - | |enunciado= | ||
| - | :Resuelve el siguiente sistema de ecuaciones por el método de Gauss: | ||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | x \, + \, y \, + \, z & = & ~~3 | ||
| - | \\ | ||
| - | x \, + \, y \, - \, z & = & ~~1 | ||
| - | \\ | ||
| - | x \, - \, y \, - \, z & = & -1 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |sol= | ||
| - | Operamos con las ecuaciones de la siguiente manera: | ||
| - | *Ecu2: <math>Ecu2-Ecu1\;</math> | ||
| - | *Ecu3: <math>Ecu3-Ecu1\;</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | x \, + \, y \, + \, ~~z & = & ~~3 | ||
| - | \\ | ||
| - | \qquad \quad - \, ~2z & = & -2 | ||
| - | \\ | ||
| - | \quad - \, 2y \, - \, 2z & = & -4 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Intercambiamos las dos últimas ecuaciones para dejar el sistema escalonado: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x \, + \, y \, + \, z & = & ~~3 | ||
| - | \\ | ||
| - | \quad -2y \, - 2z & = & -4 | ||
| - | \\ | ||
| - | \qquad \quad - \, 2z & = & -2 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | que es equivalente al inicial. | ||
| - | |||
| - | Solucionamos la tercera ocuacion para obtener <math>z\;</math>: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | z \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | En la primera y segunda ecuación, sustituimos <math>z\;</math> por la solucion de la tercera ecuación (<math>z=1\;</math>), para obtener: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x \, + \, y \, + \, 1 & = & ~~3 | ||
| - | \\ | ||
| - | \quad -2y \, - \, 2 & = & -4 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | La segunda ecuación es ahora una ecuación con una sola incognita <math>y\;</math>, que resolvemos para obtener: | ||
| - | <center> | ||
| - | <math> | ||
| - | y \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Sustituimos la incógnita <math>y\;</math> de la primera ecuación, por la solución obtenida en la segunda ecuación (<math>y=1\;</math>). Esto nos da una ecuación en <math>x\;</math>: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | x \, + \, 1 \, + \, 1 \, = \, 3 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | que al resolverla termina de darnos la solución del sistema de ecuaciones inicial: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | x \, = \, y \, = \, z \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video | ||
| - | |titulo=Gauss, el príncipe de las matemáticas | ||
| - | |duracion=22´ | ||
| - | |sinopsis=Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo. | ||
| - | |||
| - | Sin embargo la fama de este joven, Gauss le va a venir de los cielos. A finales de 1800 los astrónomos descubren un nuevo objeto celeste. No se trata de un cometa, bien podía ser el planeta buscado tantos años entre Marte y Júpiter. Por desgracia se le pierde la pista. Pero con las pocas observaciones realizadas, Gauss se pone a la tarea de deducir su órbita y señala el lugar del cielo hacia donde apuntar los telescopios un año más tarde. Y en efecto alli aparece Ceres. | ||
| - | |||
| - | Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias. | ||
| - | |video= | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/videos/gauss/gauss.htm | ||
| - | width=100% | ||
| - | height=650 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/videos/gauss/gauss.htm '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | <center>[http://c0/helvia/aula/archivos/repositorio//0/102/html/index.htm '''Click''' aquí para enlace desde servidor TIC]</center> | ||
| - | }} | ||
| - | |||
| - | ==Discusión de sistemas== | ||
| - | Después de realizar las transformaciones que se consideren pertinentes, se obtendrá un sistema escalonado. Suponiendo que hubiésemos eliminado, si las hubiera, las filas nulas (0 0 0 ... 0), que corresponden a ecuaciones del tipo 0 = 0, el sistema equivalente tendría ahora k ecuaciones lineales con n incógnitas. Analizando el sistema resultante, podemos efectuar su discusión del siguiente modo: | ||
| - | |||
| - | === Sistema incompatible (S.I.) === | ||
| - | {{Caja_Amarilla|texto= | ||
| - | Si alguna de las ecuaciones es del tipo 0 = b (siendo b distinto de cero), el sistema es '''incompatible''' y no tiene solución. | ||
| - | }} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| - | Consideremos el siguiente sistema: | ||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | ~~~x \, + \, 2y \, + \, 5z & = & -3 | ||
| - | \\ | ||
| - | ~~2x \, - \, 2y \, + \, 3z & = & ~~5 | ||
| - | \\ | ||
| - | -2x \, + \, 8y \, + \, 4z & = & -4 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Operamos de la siguiente manera: | ||
| - | *Ecu2: <math>Ecu2 - 2 \cdot Ecu1</math> | ||
| - | *Ecu3: <math>Ecu3 + 2 \cdot Ecu1</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | ~~~x \, + \, 2y \, + \, 5z & = & -3 | ||
| - | \\ | ||
| - | \qquad \, - \, ~~6y \, + \, -7z & = & ~~11 | ||
| - | \\ | ||
| - | \qquad \, + \, 12y \, + \, 14z & = & -10 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Ahora operamos con la última ecuación para terminar de escalonar: | ||
| - | *Ecu3: <math>Ecu3 + 2 \cdot Ecu2</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x \, + \, 2y \, + \, 5z & = & -3 | ||
| - | \\ | ||
| - | \quad -6y \, - 7z & = & ~11 | ||
| - | \\ | ||
| - | \qquad \quad \quad \, 0 & = & ~12 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | que es equivalente al inicial. | ||
| - | |||
| - | El sistema es incompatible pués la tercera ecuación es absurda. | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ===Sistema compatible determinado (S.C.D.)=== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | Si no hay ecuaciones del tipo 0 = b, y además k = n, es decir, el número de ecuaciones del sistema equivalente es igual al número de incógnitas, el sistema es '''compatible determinado''' y, por lo tanto, tiene una única solución. | ||
| - | }} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| - | Consideremos el siguiente sistema: | ||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | x \, + \, y \, + \, z & = & ~~3 | ||
| - | \\ | ||
| - | x \, + \, y \, - \, z & = & ~~1 | ||
| - | \\ | ||
| - | x \, - \, y \, - \, z & = & -1 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Operamos con las ecuaciones de la siguiente manera: | ||
| - | *Ecu2: <math>Ecu2-Ecu1\;</math> | ||
| - | *Ecu3: <math>Ecu3-Ecu1\;</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | x \, + \, y \, + \, ~~z & = & ~~3 | ||
| - | \\ | ||
| - | \qquad \quad - \, ~2z & = & -2 | ||
| - | \\ | ||
| - | \quad - \, 2y \, - \, 2z & = & -4 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Intercambiamos las dos últimas ecuaciones para dejar el sistema escalonado: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x \, + \, y \, + \, z & = & ~~3 | ||
| - | \\ | ||
| - | \quad -2y \, - 2z & = & -4 | ||
| - | \\ | ||
| - | \qquad \quad - \, 2z & = & -2 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | que es equivalente al inicial. | ||
| - | |||
| - | Solucionamos la tercera ocuacion para obtener <math>z\;</math>: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | z \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | En la primera y segunda ecuación, sustituimos <math>z\;</math> por la solucion de la tercera ecuación (<math>z=1\;</math>), para obtener: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x \, + \, y \, + \, 1 & = & ~~3 | ||
| - | \\ | ||
| - | \quad -2y \, - \, 2 & = & -4 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | La segunda ecuación es ahora una ecuación con una sola incognita <math>y\;</math>, que resolvemos para obtener: | ||
| - | <center> | ||
| - | <math> | ||
| - | y \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Sustituimos la incógnita <math>y\;</math> de la primera ecuación, por la solución obtenida en la segunda ecuación (<math>y=1\;</math>). Esto nos da una ecuación en <math>x\;</math>: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | x \, + \, 1 \, + \, 1 \, = \, 3 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | que al resolverla termina de darnos la solución del sistema de ecuaciones inicial: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | x \, = \, y \, = \, z \, = \, 1 | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Se trata, por tanto, de un sistema con una única solución, un S.C.D. (sistema compatible determinado). | ||
| - | }}{{p}} | ||
| - | |||
| - | ===Sistema compatible indeterminado (S.C.I.)=== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | Si no hay ecuaciones del tipo 0 = b y k < n, es decir, el número de ecuaciones es menor que el número de incógnitas, el sistema es '''compatible indeterminado''' y, en consecuencia, tiene infinitas soluciones. En este caso, tenemos que separar las incógnitas principales de las no principales. Pero, ¿cuáles son las incógnitas principales? Se puede dar el siguiente criterio: Si el sistema es escalonado y tiene k ecuaciones, las k primeras incógnitas serán las principales y las n - k restantes serán las no principales que pasaremos al segundo miembro como parámetros. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| - | Consideremos el siguiente sistema: | ||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ \begin{matrix} | ||
| - | 3x \, + \, 2y \, - \, 2z & = & ~~4 | ||
| - | \\ | ||
| - | 4x \, + \, ~y \, - \, ~z & = & ~~5 | ||
| - | \\ | ||
| - | ~x \, + \, 4y \, - \, 4z & = & -2 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | La matriz ampliada del sistema de ecuaciones es: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | A^*=\left( | ||
| - | \left. | ||
| - | \begin{matrix} | ||
| - | ~~3 & ~~2 & -2 | ||
| - | \\ | ||
| - | ~~4 & ~~1 & -1 | ||
| - | \\ | ||
| - | ~~1 & ~~4 & -4 | ||
| - | \end{matrix} | ||
| - | \right| | ||
| - | \begin{matrix} | ||
| - | ~~4 | ||
| - | \\ | ||
| - | ~~7 | ||
| - | \\ | ||
| - | -2 | ||
| - | \end{matrix} | ||
| - | \right) | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | Operamos de la siguiente manera: | ||
| - | *Fila1: <math>Fila1 - 2 \cdot Fila2</math> | ||
| - | *Fila3: <math>Fila3 -4 \cdot Fila2</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left( | ||
| - | \left. | ||
| - | \begin{matrix} | ||
| - | -5 & ~~0 & ~~0 | ||
| - | \\ | ||
| - | ~~~4 & ~~1 & -1 | ||
| - | \\ | ||
| - | -15 & ~~0 & ~~0 | ||
| - | \end{matrix} | ||
| - | \right| | ||
| - | \begin{matrix} | ||
| - | -10 | ||
| - | \\ | ||
| - | ~~7 | ||
| - | \\ | ||
| - | -30 | ||
| - | \end{matrix} | ||
| - | \right) | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | Intercambiamos Fila 1 y Fila 2: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left( | ||
| - | \left. | ||
| - | \begin{matrix} | ||
| - | ~~~4 & ~~1 & -1 | ||
| - | \\ | ||
| - | -5 & ~~0 & ~~0 | ||
| - | \\ | ||
| - | -15 & ~~0 & ~~0 | ||
| - | \end{matrix} | ||
| - | \right| | ||
| - | \begin{matrix} | ||
| - | ~~7 | ||
| - | \\ | ||
| - | -10 | ||
| - | \\ | ||
| - | -30 | ||
| - | \end{matrix} | ||
| - | \right) | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | Ahora operamos con las dos últimas filas: | ||
| - | *Fila3: <math>Fila3 - 3 \cdot Fila2</math> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left( | ||
| - | \left. | ||
| - | \begin{matrix} | ||
| - | ~~4 & ~~1 & -1 | ||
| - | \\ | ||
| - | -5 & ~~0 & ~~0 | ||
| - | \\ | ||
| - | ~~0 & ~~0 & ~~0 | ||
| - | \end{matrix} | ||
| - | \right| | ||
| - | \begin{matrix} | ||
| - | ~~7 | ||
| - | \\ | ||
| - | -10 | ||
| - | \\ | ||
| - | ~~0 | ||
| - | \end{matrix} | ||
| - | \right) | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | que es la matriz ampliada del sistema de ecuaciones: | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | 4x \, + \, y \, - \, z & = & 7 | ||
| - | \\ | ||
| - | ~x\qquad \quad \quad \, & = & 2 | ||
| - | \\ | ||
| - | \qquad \quad \quad \, 0 & = & 0 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | que es equivalente al inicial. | ||
| - | |||
| - | <br/> | ||
| - | |||
| - | La tercera ecuación se puede suprimir y de la segunda ecuación tenemos que <math>x=2\;</math>. | ||
| - | |||
| - | Sustituyendo el valor <math>x=2\;</math> en la primera ecuación, ésta queda: | ||
| - | <center><math>8+y-z=7\;</math></center> | ||
| - | |||
| - | y simplificada: | ||
| - | |||
| - | <center><math>y-z=-1\;</math></center> | ||
| - | |||
| - | Así nuestro sistema es equivalente a otro con una sola ecuación y dos incógnitas, que por tanto tiene infinitas soluciones, que podemos expresar de la siguiente forma: | ||
| - | |||
| - | <center> | ||
| - | <math> | ||
| - | \left\{ | ||
| - | \begin{matrix} | ||
| - | x & = & 2 | ||
| - | \\ | ||
| - | y & = & z-1 | ||
| - | \end{matrix} | ||
| - | \right. | ||
| - | </math> | ||
| - | </center> | ||
| - | |||
| - | Se trata de un sistema compatrible indeterminado. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Método de Gauss''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Discusión y resolución de sistemas por el método de Gauss. | ||
| - | |actividad= | ||
| - | La siguiente escena efectúa la discusión y resuelve, en los casos que proceda (sistema compatible determinado o indeterminado), cualquier sistema de ecuaciones lineales, utilizando el método de Gauss. El número máximo de ecuaciones y de incógnitas que puede tener el sistema es 5. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_2/Gauss/metodo_de_gauss_1.html | ||
| - | width=100% | ||
| - | height=675 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_2/Gauss/metodo_de_gauss_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(pág. 83-85)
Sistema escalonado
Consideremos un sistema de ecuaciones lineales n x m (n ecuaciones y m incógnitas) en el que cada ecuación tiene sus términos ordenados por incógnitas y las ecuaciones organizadas por filas. Este sistema se dice que es escalonado si la ecuación de la fila n carece, al menos, de las n - 1 primeras incógnitas. Si además tiene el mismo número de ecuaciones que de incógnitas (n = m), el sistema se dice que es escalonado triangular.
El interés de los sistemas escalonados radica en que son mucho más fáciles de resolver.
Ejemplo 1: El siguiente sistema es escalonado triangular:
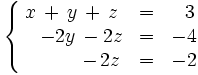
Fíjate que para resolver este sistema, basta con despejar la incógnita z de la tercera ecuación, obteniendose z = 1. Posteriormente, sustituyendo dicho valor de z en la segunda ecuación, es posible despejar fácilmente la incógnita y, resultando y = 1. Finalmente, sustituyendo los valores de z e y en la primera ecuación , se despeja x sin mayor problema, y tendríamos que x = 1.
Ejemplo 2: También es escalonado, aunque no triangular, este otro:
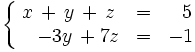
La resolución de sistemas como este requiere el uso de parámetros y se verá más adelante.
Ejemplo 3: El siguiente sistema, aunque no es escalonado según la definición dada, a efectos prácticos podemos considerar que lo es, ya que, mediante un simple reordenamiento de ecuaciones e incógnitas, podemos conseguir que lo sea.

Método reducción de Gauss
El método de Gauss, que se debe al matemático alemán Johann Carl Friedrich Gauss, es un método para resolver sistemas de ecuaciones lineales n x m que generaliza al método de reducción usado para sistemas 2 x 2. Consiste en la aplicación sucesiva del método de reducción, utilizando los criterios de equivalencia de sistemas, para transformar el sistema de ecuaciones en un sistema escalonado, por tanto, más fácil de resolver.
Vídeo de introducción al método de Gauss que ilustra las ventajas de los sistemas escalonados para resolver sistemas de ecuaciones lineales.
Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo.
Sin embargo la fama de este joven, Gauss le va a venir de los cielos. A finales de 1800 los astrónomos descubren un nuevo objeto celeste. No se trata de un cometa, bien podía ser el planeta buscado tantos años entre Marte y Júpiter. Por desgracia se le pierde la pista. Pero con las pocas observaciones realizadas, Gauss se pone a la tarea de deducir su órbita y señala el lugar del cielo hacia donde apuntar los telescopios un año más tarde. Y en efecto alli aparece Ceres.
Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias.
Criterios de equivalencia de sistemas
Los criterios de equivalencia de sistemas nos dicen las "operaciones" que podemos realizar sobre las ecuaciones del sistema inicial para transformarlo en otro equivalente. Son los siguientes:
- Multiplicar o dividir una ecuación por un número real distinto de cero.
- Sumar o restar a los dos miembros de una ecuación la misma expresión.
- Sumarle a una ecuación otra ecuación multiplicada por un número. (Como caso particular: Sumarle o restarle a una ecuación otra ecuación)
- Cambiar el orden de las ecuaciones.
- Cambiar el orden de las incógnitas del sistema.
- Eliminar ecuaciones nulas (0=0).
- Eliminar una ecuación que sea idéntica o proporcional a otra.
Ejemplo: Método de reducción de Gauss
Resuelve el siguiente sistema de ecuaciones por el método de Gauss:
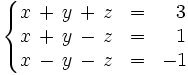
Operamos con las ecuaciones de la siguiente manera:
-
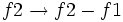 (Sustituimos la ecuación de la fila 2 por la que resulta de restar la de la fila 2 menos la de la fila 1)
(Sustituimos la ecuación de la fila 2 por la que resulta de restar la de la fila 2 menos la de la fila 1)
-
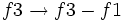 (Sustituimos la ecuación de la fila 3 por la que resulta de restar la de la fila 3 menos la de la fila 1)
(Sustituimos la ecuación de la fila 3 por la que resulta de restar la de la fila 3 menos la de la fila 1)
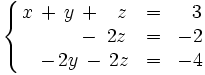
-
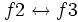 (Intercambiamos la ecuación de la fila 2 por la de la fila 3)
(Intercambiamos la ecuación de la fila 2 por la de la fila 3)
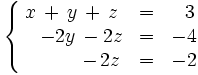
para obtener un sistema escalonado equivalente al inicial.
Resolvemos la tercera ecuacion para obtener 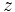 :
:
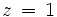
En la primera y segunda ecuación, sustituimos 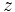 por la solucion que acabamos de obtener:
por la solucion que acabamos de obtener:
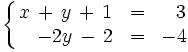
Resolvemos la tercera ecuacion para obtener  :
:
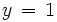
Sustituimos la incógnita  de la primera ecuación, por la solución que acabamos de obtener. Esto nos da el valor de
de la primera ecuación, por la solución que acabamos de obtener. Esto nos da el valor de  :
:
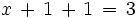
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
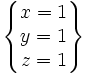
Método de Gauss para resolver sistemas de tres ecuaciones con tres incógnitas o más.
Resuelve por el método de Gauss:
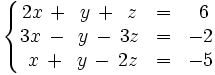
Resuelve por el método de Gauss:
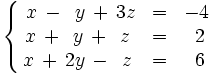
Continuación del video anterior.
Resuelve por el método de Gauss:
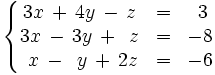
Continuación del video anterior.
Resuelve por el método de Gauss:
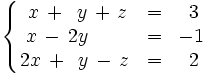
Continuación del video anterior.
Discusión de sistemas
Discutir un sistema es determinar si tiene solución y, caso de tenerla, saber si ésta es única.
- Si el sistema no tiene solución, diremos que es un sistema incompatible (S.I.)
- Si el sistema tiene solución, diremos que es un sistema compatible (S.C.)
- Si la solución es única, diremos que es un sistema compatible determinado (S.C.D.)
- Si la solución no es única, diremos que es un sistema compatible indeterminado (S.C.I.)
Discusión de sistemas lineales
Consideremos un sistema de ecuaciones lineales n x m, que tras realizar las transformaciones oportunas está escalonado. Suponiendo que hubiésemos eliminado las filas nulas, si las hubiera, que corresponden a ecuaciones del tipo 0 = 0, el sistema equivalente tendría ahora k ecuaciones lineales con m incógnitas, con 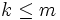 . Analizando el sistema resultante, podemos efectuar su discusión del siguiente modo:
. Analizando el sistema resultante, podemos efectuar su discusión del siguiente modo:
- Sistema incompatible (S.I.): Si alguna de las ecuaciones que quedan son del tipo 0 = b (siendo b distinto de cero), el sistema es incompatible y no tiene solución.
Consideremos el siguiente sistema:
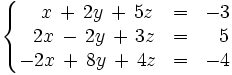
Operamos de la siguiente manera:
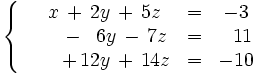
Ahora operamos con la última ecuación para terminar de escalonar:
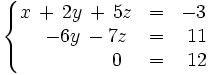
que es equivalente al inicial.
El sistema es incompatible pués la tercera ecuación es absurda.
- Sistema compatible determinado (S.C.D.): Si no hay ecuaciones del tipo 0 = b (con b distinto de cero), y además k = m, es decir, el número de ecuaciones del sistema equivalente es igual al número de incógnitas, el sistema es compatible determinado y, por lo tanto, tiene una única solución.
Consideremos el siguiente sistema:
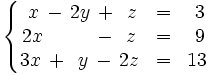
Reordenamos las ecuaciones y las incógnitas de la siguiente manera:
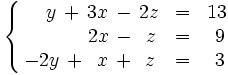
Operamos con la primera y tercera ecuación:
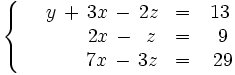
Intercambiamos las incógnitas de la segunda y tercer columna:
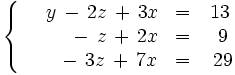
Operamos con la segunda y tercera ecuación:
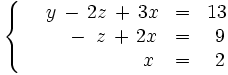
De la tercera ecuacion tenemos el valor  .
.
En la segunda ecuación, sustituimos  , para obtener
, para obtener 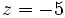 .
.
Y, finalmente, en la primera ecuación sustituimos  y
y 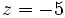 , para hallar
, para hallar 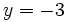 .
.
Así tenemos que la solución del sistema de ecuaciones inicial es:
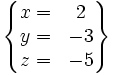
Se trata, por tanto, de un sistema con una única solución, un S.C.D. (sistema compatible determinado).
- Sistema compatible indeterminado (S.C.I.): Si no hay ecuaciones del tipo 0 = b, y además k < m, es decir, el número de ecuaciones es menor que el número de incógnitas, el sistema es compatible indeterminado y, en consecuencia, tiene infinitas soluciones. En este caso, tenemos que separar las incógnitas o "variables principales" de las no principales (también llamadas "variables libres"). Pero, ¿cuáles son las incógnitas principales? Las podemos elegir como queramos aunque podemos dar el siguiente criterio: Si el sistema es escalonado y tiene k ecuaciones, las k últimas incógnitas serán las "principales" y las m - k primeras serán las "libres", que pasaremos al segundo miembro como parámetros. No obstante, este criterio puede variarse según convenga.
Consideremos el siguiente sistema:
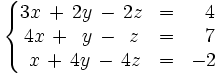
Intercambiamos la fila 1 con la 2; y la columna 1 con la 2;
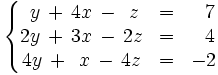
Operamos de la siguiente manera:
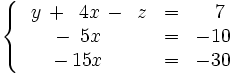
Operamos con las filas 2 y 3:
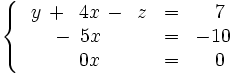
Eliminamos la tercera fila por ser del tipo 0=0:
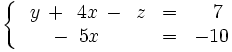
Simplificamos por 5 la segunda ecuación:
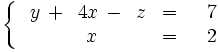
Es un sistema escalonado sin ecuaciones del tipo 0=0 ó 0=b (con b no nulo), con k=2 ecuaciones y m=3 incógnitas, por lo que tendremos 3-2=1 parámetro. Usaremos como parámetro, por ejemplo, la incógnita z, por lo que tendremos que expresar las otras incógnitas en función de z.
Sustituyendo el valor x = 2 en la primera ecuación, nos queda:
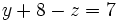
Despejando y :
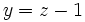
Así, las soluciones del sistema, expresadas en función del parámetro z, son:
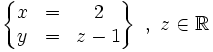
Para cada valor del parámetro z se obtiene una solución del sistema. Por tanto, el sistema tiene infinitas soluciones y se trata de un sistema compatible indeterminado.
Para enfatizar que z es un parámetro, éste suele sustituirse por otra letra, por ejemplo λ, aunque no es obligatorio. Así, la expresión paramétrica de la solución del sistema quedaría:
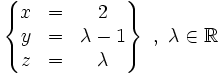
También pueden expresarse las soluciones del sistema mediante ternas de números reales:
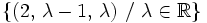
Sistemas Compatibles Indeterminados: qué son, cómo se identifican con el método de Gauss y cómo se resuelven.
Sistemas Incompatibles. Cómo se identifican con el método de Gauss y ejemplos.
Tipos de sistemas de ecuaciones lineales atendiendo al número de soluciones.
Discute y resuelve por el método de Gauss el siguiente sistema:
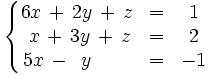
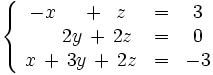
Discute y resuelve por el método de Gauss el siguiente sistema:
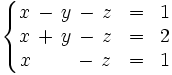
Discute y resuelve por el método de Gauss el siguiente sistema:
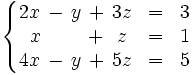
Continuación del video anterior.
Discute y resuelve por el método de Gauss el siguiente sistema:
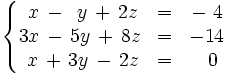
Continuación del video anterior.
Resuelve por el método de Gauss:
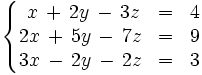
Resuelve por el método de Gauss:
1. 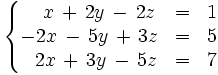
2. 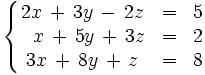
Resuelve por el método de Gauss:
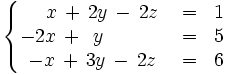
Discute y resuelve el siguiente sistema:
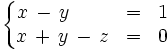
Método de Gauss con matrices
El método de Gauss se puede abreviar utilizando matrices. Estas agilizan el proceso de escalonamiento, ya que, en cada transformación de las ecuaciones del sistema, éstas no se escriben completas, sino sólo los coeficientes de las mismas.
Discute y resuelve por el método de Gauss el siguiente sistema:
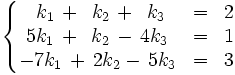
Discute y resuelve por el método de Gauss el siguiente sistema:
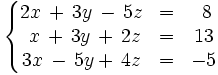
Discute y resuelve por el método de Gauss el siguiente sistema:
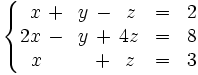
Discute y resuelve por el método de Gauss el siguiente sistema:
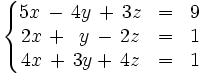
Discute y resuelve por el método de Gauss el siguiente sistema:
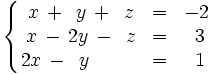
Discute y resuelve por el método de Gauss el siguiente sistema:
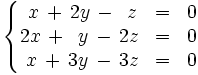
Resuelve por el método de Gauss:
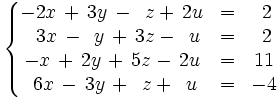
Resuelve por el método de Gauss:
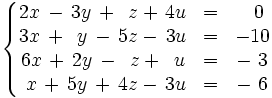
Resuelve por el método de Gauss el siguiente sistema:
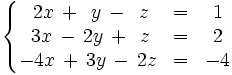
Sistemas escalonados. Expresión matricial. Discusión y resolución en sus distintos casos.
Resolución de S.C.I. expresados matricialmente. Ejemplos y ejercicios.
Obtención de una de las infinitas soluciones de un S.C.I. Ejemplos y ejercicios.
Número de variables libres de un sistema escalonado.
Nota: En el video no se menciona, pero se sobreentiende que el sistema debe estar escalonado y no poseer ecuaciones del tipo 0 = b (con b no nulo) para aplicar los razonamientos que en él se hacen.
Resolución de sistemas por el método de Gauss usando matrices.
|
Actividad: Resolución de sistemas lineales Escalona y resuelve el siguiente sistema 3x3: 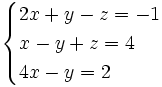 Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: solve 2x+y-z=-1, x-y+z=4, 4x-y=2 o en formato matricial: solve {{2,1,-1},{1,-1,1},{4,-1,0}}*{x,y,z}={-1,4,2} y si nos interesa ver como queda la matriz escalonada: row reduce {{2,1,-1,-1},{1,-1,1,4},{4,-1,0,2}} |
Método de Gauss-Jordan
Método de Gauss-Jordan
Consideremos un sistema de ecuaciones lineales n x n. En el método de Gauss realizabamos una triangulación superior del sistema de ecuaciones lineales, haciendo ceros por debajo de la diagonal. Si continuamos el método de Gauss haciendo ceros en la parte superior de la diagonal, conseguiremos un sistema equivalente cuyas ecuaciones tienen una sola incógnita (la de la diagonal). A este método se le conoce como método de Gauss-Jordan, pues debe su nombre a los matemáticos Carl Friedrich Gauss y a Wilhelm Jordan.
Resuelve por el método de Gauss-Jordan el siguiente sistema:
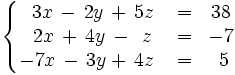
Resuelve por el método de Gauss-Jordan el siguiente sistema:
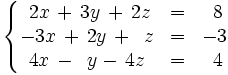
Resuelve por el método de Gauss-Jordan el siguiente sistema:
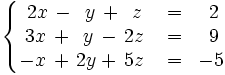
Continuación del ejercicio 1a.
Resuelve por el método de Gauss-Jordan el siguiente sistema:
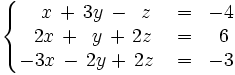
Resuelve por el método de Gauss-Jordan:
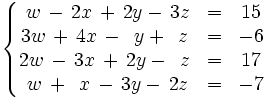
Resuelve por el método de Gauss-Jordan:
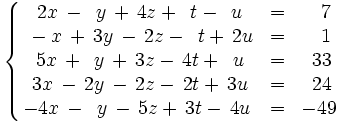
Discusión de sistemas lineales con parámetros
Discutir un sistema de ecuaciones lineales con parámetros consiste en determinar el valor de los parámetros que hacen que el sistema sea S.C.D., S.I. o S.C.I.
Discute el siguiente sistema en función del parámetro k:
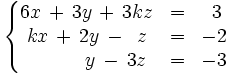
Discute el siguiente sistema en función del parámetro a:
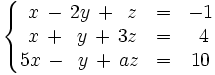
Discute los siguientes sistemas en función del parámetro m:
Discute el siguiente sistema en función del parámetro a:
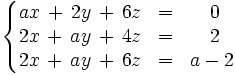
Discute el siguiente sistema en función del parámetro a:
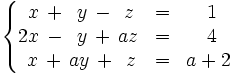
Discute el siguiente sistema en función de los parámetros a y b:
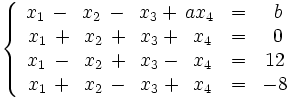
Halla el valor de k para que el sistema no tenga solución:
1. 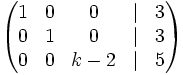 2.
2. 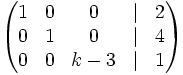 3.
3. 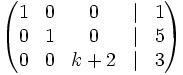
Halla el valor de k para que el sistema tenga infinitas soluciones:
1. 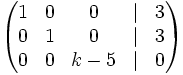 2.
2. 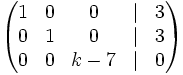 3.
3. 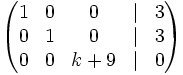
Discute el sistema en función del parámetro k:
1. 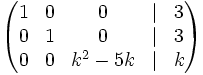 2.
2. 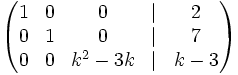 3.
3. 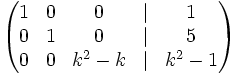
Discute el siguiente sistema en función del parámetro k:
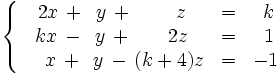
Ejercicios propuestos
|
Ejercicios propuestos: Método de Gauss |