Vectores: Definición y operaciones (1ºBach)
De Wikipedia
| Revisión de 19:36 13 mar 2009 Coordinador (Discusión | contribuciones) (→Combinación lineal de vectores) ← Ir a diferencia anterior |
Revisión de 19:50 13 mar 2009 Coordinador (Discusión | contribuciones) (→Combinación lineal de vectores) Ir a siguiente diferencia → |
||
| Línea 143: | Línea 143: | ||
| <center><math>\overrightarrow{w}=a \cdot \overrightarrow{u}+ b \cdot \overrightarrow{v}+ c \cdot \overrightarrow{v}</math></center> | <center><math>\overrightarrow{w}=a \cdot \overrightarrow{u}+ b \cdot \overrightarrow{v}+ c \cdot \overrightarrow{v}</math></center> | ||
| + | {{p}} | ||
| |celda2=<center>[[Imagen:combilinealvectores.jpg|300px]]</center> | |celda2=<center>[[Imagen:combilinealvectores.jpg|300px]]</center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{AI2|titulo=Actividad interactiva: ''Vectores''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' Módulo, dirección y sentido de un vector fijo. | ||
| + | {{p}} | ||
| + | |actividad=En la escena siguiente se van a dibujar los vectores u = 4x + 2y, y v = -2x + y | ||
| + | Se dice entonces que los vectores u y v son combinación lineal de x e y. | ||
| + | Veamos cómo: | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores4_2.html | ||
| + | width=430 | ||
| + | height=390 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores4_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | '''Ejercicio 1: u = 4x + 2y''' | ||
| + | |||
| + | #Cambia el valor de n a n=4. Así se obtiene el vector 4x | ||
| + | #Cambia el valor de m a m=2. Así se obtiene el vector 2y | ||
| + | #Arrastra el punto B, trazando una paralela al vector y | ||
| + | #Arrastra el punto C, trazando una paralela al vector x | ||
| + | #Prolongando estas paralelas suficientemente obtienes un paralelogramo cuyos lados son los vectores 4x y 2y. Arrastra el punto A para dibujar la diagonal que representa al vector u = 4x + 2y | ||
| + | |||
| + | '''Ejercicio 2: v = -2x + y''' | ||
| + | |||
| + | |||
| + | #Ahora le das a n = -2 para dibujar el vector -2x | ||
| + | #Arrastra el punto D, trazando una paralela al vector y | ||
| + | #Arrastra el punto E, trazando una paralela al vector x | ||
| + | #Prolongando estas paralelas suficientemente obtienes una paralelogramo cuyos lados son los vectores -2x e y. Arrastra el punto A, de nuevo, para dibujar la diagonal que representa al vector v = -2x + y | ||
| + | }} | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 19:50 13 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Vectores
Vectores fijos
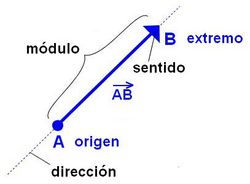
Un vector fijo es un segmento orientado que queda determinado por un punto origen, A y otro punto extremo, B. Lo simbolizamos Características de un vector:
|
Vectores opuestos
Dos vectores, |
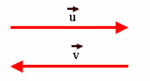
Vectores equipolentes. Vectores libres
Dos vectores, Dado un vector, existen infinitos vectores equipolentes a él. Cuando queremos hacer uso de un vector podemos elegir uno de esos infinitos vectores iguales a él y utilizarlo como representante del vector. Al conjunto de todos los vectores equipolentes a uno dado se le llama vector libre. Un vector libre lo denotaremos mediante una letra con una flecha: |
|
Actividad interactiva: Vectores Actividad 1: Módulo, dirección y sentido de un vector fijo. Actividad: En la escena puedes ver varios vectores fijos.
Actividad 2: Vectores equipolentes. Actividad: Dos vectores fijos son equipolentes si tienen el mismo módulo, dirección y sentido. Para comprobarlo, se unen sus orígenes y sus extremos respectivos. Si el polígono resultante es un paralelogramo, los vectores son equipolentes.
Actividad 3: Vectores libres. Actividad: Encierra en cada caja los vectores que te parezcan equipolentes al que ya está dentro. (Para ello pincha y arrastra el puntito negro que ves en el origen de cada vector. Puedes usar el zoom si lo necesitas.) ¿Cuántos vectores libres se obtienen? |
Operaciones con vectores
Producto de un vector por un número
El producto de un número real
|
Suma y resta de vectores
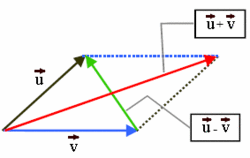
| Suma de vectores:
Dados dos vectores |
| Resta de vectores:
Para restar dos vectores |
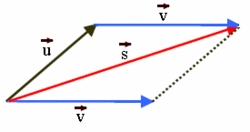
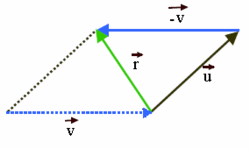
| Método del paralelogramo:
Si consideramos el paralelogramo que resulta de los vectores |
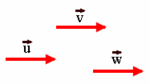
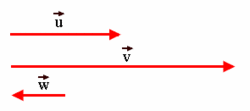
Combinación lineal de vectores
Dados dos vectores 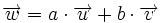 En el gráfigo de la derecha tenemos un ejemplo en el que el vector La definición anterior se puede extender a mas de dos vectores, así, por ejemplo, un vector 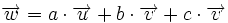 |
|
Actividad interactiva: Vectores Actividad 1: Módulo, dirección y sentido de un vector fijo. Actividad: En la escena siguiente se van a dibujar los vectores u = 4x + 2y, y v = -2x + y Se dice entonces que los vectores u y v son combinación lineal de x e y. Veamos cómo: Ejercicio 1: u = 4x + 2y
Ejercicio 2: v = -2x + y
|
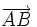
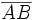
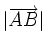
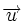
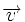
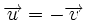
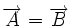
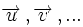
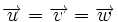
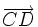 son equipolentes. Para ello pincha y arrastra los puntitos amarillos que ves en A y B.
son equipolentes. Para ello pincha y arrastra los puntitos amarillos que ves en A y B.
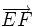 y
y 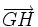 son equipolentes.
son equipolentes.
 por un vector
por un vector 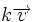
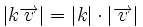
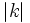 es el valor absoluto del número real
es el valor absoluto del número real 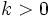 y opuesto si
y opuesto si 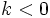 .
.
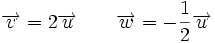
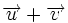
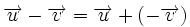 .
.
 y
y 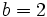 .
.