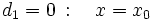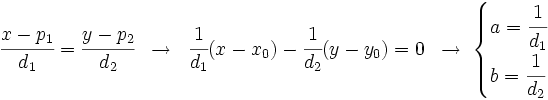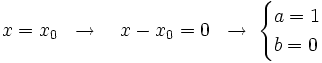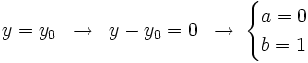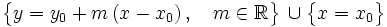Haz de rectas en el plano (1ºBach)
De Wikipedia
| Revisión de 17:57 19 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:20 19 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Haz de rectas de centro un punto== | ==Haz de rectas de centro un punto== | ||
| - | {{Caja_Amarilla|texto=Llamamos '''haz de rectas de centro P''' al conjunto de todas las rectas que pasan por un punto P. | + | {{Tabla75|celda2=<center>[[Imagen:hazrectas.png|200px]]</center> |
| + | |celda1={{Caja_Amarilla|texto=Llamamos '''haz de rectas de centro P''' al conjunto de todas las rectas que pasan por un punto P. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 30: | Línea 31: | ||
| :'''c)'''{{b4}}<math>y=y_0 \;\; \rightarrow \;\; y-y_0=0 \;\; \rightarrow \; \begin{cases} a=0 \\ b=1 \end{cases}</math> | :'''c)'''{{b4}}<math>y=y_0 \;\; \rightarrow \;\; y-y_0=0 \;\; \rightarrow \; \begin{cases} a=0 \\ b=1 \end{cases}</math> | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:20 19 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
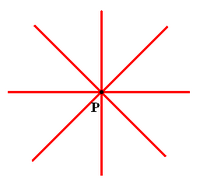
Haz de rectas de centro un punto
Llamamos haz de rectas de centro P al conjunto de todas las rectas que pasan por un punto P. Proposición El haz de rectas de centro
Los parámetros Demostración: Es evidente que cualquier recta del haz pasa por el punto P, puesto que al sustituir las coordenadas del punto en la expresión del haz, siempre se verifica la ecuación. Faltaría ver si cualquier recta que pase por el punto P se puede expresar como recta del haz. Para ello, consideremos una recta cualquiera que pase por el punto P. La ecuación de ésta será:
Cada uno de estos tres casos se puede poner como una recta del haz, para valores de
|
Haz de rectas de centro un punto (usando la pendiente como parámetro)
Proposición
El haz de rectas de centro 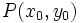 es :
es :
|
|
La pendiente  es un parámetro que, al darle valores, nos permite obtener las distintas ecuaciones de las rectas que constituyen el haz.
es un parámetro que, al darle valores, nos permite obtener las distintas ecuaciones de las rectas que constituyen el haz.
Es evidente ya que la ecuación punto pendiente permite obtener la ecuación de una recta conocido eun punto y su pendiente. Así, si yo dejo fijo al punto y hago variar la pendiente, obtengo todas las rectas con todas las inclinaciones posibles que pasan por ese punto, a falta de
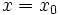 , que al ser vertical se escapa a este procedimiento, ya que su pendiente es "infinita".
, que al ser vertical se escapa a este procedimiento, ya que su pendiente es "infinita".|
Actividad interactiva: Haz de rectas de centro un punto
Actividad 1: En la siguiente escena representaremos el haz de rectas de centro un punto.
Actividad: Modifica la pendiente y observa como se obtienen las distintas ecuaciones del haz de rectas de centro P(5,4):
|
Haz de rectas de centro el punto de corte de dos rectas secantes
Proposición
Dadas dos rectas que se corten en un punto P: 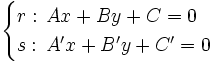 .
.
La ecuación del haz de centro P es:
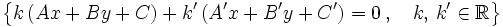
|
Lo parámetros  y
y 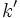 , al darles valores, nos permiten obtener las distintas ecuaciones de las rectas que constituyen el haz, siempre que no sean simultaneamente nulos.
, al darles valores, nos permiten obtener las distintas ecuaciones de las rectas que constituyen el haz, siempre que no sean simultaneamente nulos.
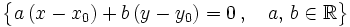
 y
y  , al darles valores, nos permiten obtener las distintas ecuaciones de las rectas que constituyen el haz, siempre que no sean simultaneamente nulos.
, al darles valores, nos permiten obtener las distintas ecuaciones de las rectas que constituyen el haz, siempre que no sean simultaneamente nulos.
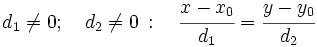 (ecuación continua)
(ecuación continua)