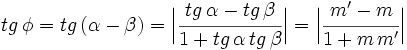Ángulo entre dos rectas del plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:47 23 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:56 23 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| (*) '''Nota:''' En el caso en que sean perpendiculares, el producto escalar del numerador es cero y la igualdad queda <math>cos \, \alpha=0</math>, de donde <math>\alpha=90^\circ</math>. | (*) '''Nota:''' En el caso en que sean perpendiculares, el producto escalar del numerador es cero y la igualdad queda <math>cos \, \alpha=0</math>, de donde <math>\alpha=90^\circ</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Ángulo entre dos rectas a partir de sus pendientes== | ||
| + | {{Teorema|titulo=Proposición|enunciado=:Dadas dos rectas con pendientes <math>m\,</math> y {{sube|porcentaje=+20%|contenido=<math>m'\,</math>}}. Se verifica que | ||
| + | |||
| + | <center><math>tg \, \phi = \Big| \cfrac{m'-m}{1+m \,m'} \Big|</math></center> | ||
| + | |demo= | ||
| + | Teniendo en cuenta que <math>m=tg \, \alpha</math> y <math>m'=tg \, \beta</math>, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: | ||
| + | |||
| + | :<math>tg \, \phi=tg \, (\alpha - \beta)= \Big| \cfrac{tg \, \alpha - tg \, \beta}{1+tg \, \alpha \, tg \, \beta} \Big|= \Big| \cfrac{m'-m}{1+m \,m'} \Big|</math> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:56 23 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ángulo entre dos rectas
El ángulo entre dos rectas del plano es el menor de los dos ángulos que forman éstas entre sí.
Ángulo entre dos rectas a partir de sus vectores de dirección
Proposición
- Dadas dos rectas con vectores de dirección
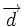 y
y 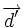 , y sea
, y sea  el ángulo que forman. Se verifica que
el ángulo que forman. Se verifica que
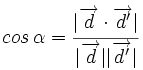
Demostración:
Sabemos que el coseno del ángulo entre dos vectores se obtiene de la siguiente manera:
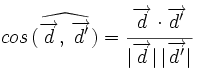
De los dos ángulos que forman las dos rectas, uno es agudo (el menor) y otro es obtuso (el mayor), salvo que sean perpendicualares (*). Nosotros cogeremos el menor de ellos, es decir, el agudo. Cómo el coseno de un ángulo agudo es positivo, tomaremos valor absoluto en el miembro de la derecha, para conseguir que así el ángulo sea el menor:
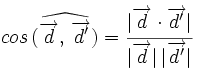
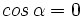 , de donde
, de donde 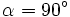 .
.Ángulo entre dos rectas a partir de sus pendientes
Proposición
- Dadas dos rectas con pendientes
 y
y 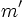 . Se verifica que
. Se verifica que
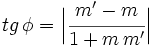
Demostración:
Teniendo en cuenta que 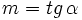 y
y 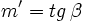 , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos:
, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: