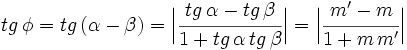Ángulo entre dos rectas del plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:08 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ángulo entre dos rectas a partir de sus pendientes) ← Ir a diferencia anterior |
Revisión de 10:13 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ángulo entre dos rectas a partir de sus vectores de dirección) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| {{p}} | {{p}} | ||
| ==Ángulo entre dos rectas a partir de sus vectores de dirección== | ==Ángulo entre dos rectas a partir de sus vectores de dirección== | ||
| + | {{Tabla75|celda2=[[Imagen:angrectas.png]]|celda1= | ||
| {{Teorema|titulo=Proposición|enunciado=:Dadas dos rectas con vectores de dirección {{sube|porcentaje=+40%|contenido=<math>\overrightarrow{d}</math>}} y {{sube|porcentaje=+40%|contenido=<math>\overrightarrow{d'}</math>}}, y sea <math>\alpha \,</math> el ángulo que forman. Se verifica que | {{Teorema|titulo=Proposición|enunciado=:Dadas dos rectas con vectores de dirección {{sube|porcentaje=+40%|contenido=<math>\overrightarrow{d}</math>}} y {{sube|porcentaje=+40%|contenido=<math>\overrightarrow{d'}</math>}}, y sea <math>\alpha \,</math> el ángulo que forman. Se verifica que | ||
| Línea 25: | Línea 26: | ||
| (*) '''Nota:''' En el caso en que sean perpendiculares, el producto escalar del numerador es cero y la igualdad queda <math>cos \, \alpha=0</math>, de donde <math>\alpha=90^\circ</math>. | (*) '''Nota:''' En el caso en que sean perpendiculares, el producto escalar del numerador es cero y la igualdad queda <math>cos \, \alpha=0</math>, de donde <math>\alpha=90^\circ</math>. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ángulo entre dos rectas a partir de sus pendientes== | ==Ángulo entre dos rectas a partir de sus pendientes== | ||
| {{Teorema|titulo=Proposición|enunciado=:Dadas dos rectas con pendientes <math>m\,</math> y {{sube|porcentaje=+20%|contenido=<math>m'\,</math>}}. Se verifica que | {{Teorema|titulo=Proposición|enunciado=:Dadas dos rectas con pendientes <math>m\,</math> y {{sube|porcentaje=+20%|contenido=<math>m'\,</math>}}. Se verifica que | ||
Revisión de 10:13 23 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ángulo entre dos rectas
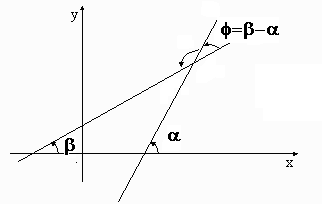
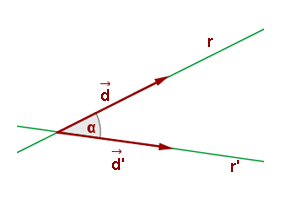
El ángulo entre dos rectas del plano es el menor de los dos ángulos que forman éstas entre sí.
Ángulo entre dos rectas a partir de sus vectores de dirección
Ángulo entre dos rectas a partir de sus pendientes
Proposición
- Dadas dos rectas con pendientes
 y
y 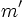 . Se verifica que
. Se verifica que
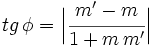
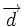
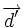
 el ángulo que forman. Se verifica que
el ángulo que forman. Se verifica que
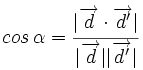
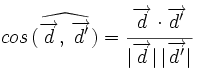
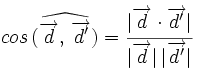
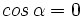 , de donde
, de donde 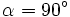 .
.
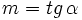 y
y 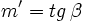 , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos:
, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: