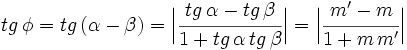Ángulo entre dos rectas del plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 15:19 23 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:22 23 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| - | {{p}}{{{dominio}}} | + | {{p}} |
| ==Ángulo entre dos rectas== | ==Ángulo entre dos rectas== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 55: | Línea 55: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://{{dominio}}/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_3_3.html | + | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_3_3.html |
| width=490 | width=490 | ||
| height=410 | height=410 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://{{dominio}}/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_3_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_3_3.html '''Click''' aquí si no se ve bien la escena]</center> |
| '''Ejercicio:''' | '''Ejercicio:''' | ||
Revisión de 15:22 23 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ángulo entre dos rectas
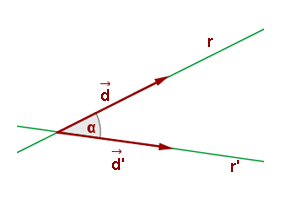
El ángulo entre dos rectas del plano es el menor de los dos ángulos que forman éstas entre sí.
Ángulo entre dos rectas a partir de sus vectores de dirección
|
Actividad interactiva: Ángulo entre dos rectas Actividad 1: Halla el ángulo que forman dos rectas dadas en ecuaciones paramétricas y utiliza la escena para comprobar los resultados. Actividad: Vamos a hallar el ángulo que forman las rectas: Sus vectores de dirección son: 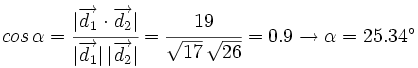
Ejercicio: Halla el ángulo que forman las rectas siguientes y comprueba los resultados en la escena anterior: |
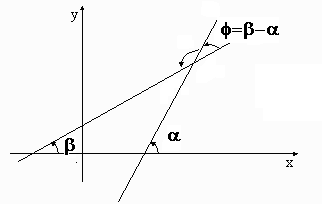
Ángulo entre dos rectas a partir de sus pendientes
Proposición
- Dadas dos rectas con pendientes
 y
y 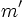 . Se verifica que
. Se verifica que
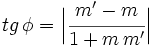
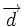
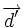
 el ángulo que forman. Se verifica que
el ángulo que forman. Se verifica que
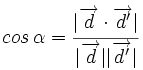
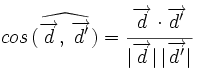
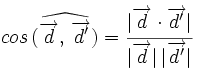
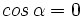 , de donde
, de donde 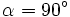 .
.
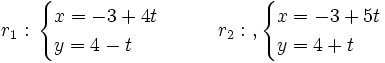
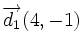
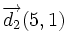
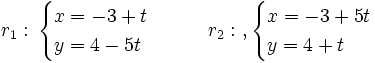
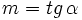 y
y 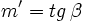 , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos:
, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: