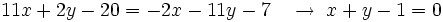Lugares geométricos (1ºBach)
De Wikipedia
| Revisión de 17:51 23 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:05 23 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 39: | Línea 39: | ||
| <center><iframe> | <center><iframe> | ||
| url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_8_1.html | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_8_1.html | ||
| - | width=440 | + | width=500 |
| - | height=370 | + | height=400 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| Línea 82: | Línea 82: | ||
| <center><iframe> | <center><iframe> | ||
| url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_8_2.html | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_8_2.html | ||
| - | width=440 | + | width=500 |
| - | height=370 | + | height=400 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
Revisión de 19:05 23 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Lugar geométrico
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
Vamos a estudiar a continuación algunos lugares geométricos como la mediatriz de un segmento o la bisectriz de un ángulo. En cada caso buscaremos una ecuación que describa a dicho lugar geométrico.
Mediatriz de un segmento
La mediatriz de un segmento 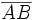 , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 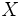 , que equidistan de los extremos
, que equidistan de los extremos 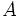 y
y 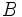 .
.
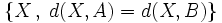
|
Actividad interactiva: Mediatriz de un segmento
Actividad 1: En la siguiente escena hallaremos la ecuación de la mediatriz del segmento de extremos
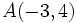 y y 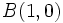 y la representaremos gráficamente. y la representaremos gráficamente.Actividad: Para hallar la ecuación del lugar geométrico 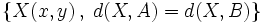 escribiremos la fórmula de la distancia entre dos puntos: 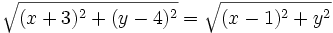 Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación: 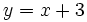 Por tanto, la mediatriz del segmento es una recta.
|
Bisectriz de un ángulo
La bisectriz de un ángulo de lados  y
y 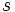 , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 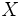 , que equidistan de los lados xtremos
, que equidistan de los lados xtremos  y
y 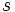 .
.
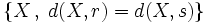
|
Actividad interactiva: Bisectriz de un ángulo
Actividad 1: En la siguiente escena hallaremos la ecuación de la bisectriz del ángulo que forman las rectas
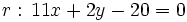 y y 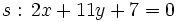 , y la representaremos gráficamente. , y la representaremos gráficamente.Actividad: Para hallar la ecuación del lugar geométrico 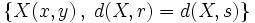 escribiremos la fórmula de la distancia de un punto a una recta: 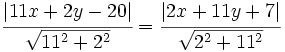 De aquí salen dos ecuaciones, ya que si Así, las dos ecuaciones resultantes son: o bien Por tanto la bisectriz de un ángulo es una recta, o mejor dicho, un par de rectas perpendiculares. En la siguiente escena tienes representadas en rojo la segunda y en gris la primera.
|
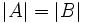 , se puede dar que
, se puede dar que 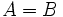 o que
o que 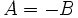 :
: