La elipse (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:24 30 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:26 30 mar 2009 Coordinador (Discusión | contribuciones) (→Elementos de la elipse) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| *<math>a=\overline{OA}=\overline{OA'}</math> semieje mayor. | *<math>a=\overline{OA}=\overline{OA'}</math> semieje mayor. | ||
| *<math>b=\overline{OB}=\overline{OB'}</math> semieje menor. | *<math>b=\overline{OB}=\overline{OB'}</math> semieje menor. | ||
| - | *<math>c=\overline{OF}=\overlin{OF'}</math> semidistancia focal. | + | *<math>c=\overline{OF}=\overline{OF'}</math> semidistancia focal. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 27: | Línea 27: | ||
| <center><math>k=\overline{AF}+\overline{AF'}=\overline{AF}+\overline{A'F}=2a</math></center> | <center><math>k=\overline{AF}+\overline{AF'}=\overline{AF}+\overline{A'F}=2a</math></center> | ||
| - | *Por ser B\, un punto de la elipse: | + | *Por ser <math>B\,</math> un punto de la elipse: |
| <center><math>\overline{BF}+\overline{BF'}=2a \rightarrow \overline{BF}=\overline{BF'}=a</math></center> | <center><math>\overline{BF}+\overline{BF'}=2a \rightarrow \overline{BF}=\overline{BF'}=a</math></center> | ||
| Línea 37: | Línea 37: | ||
| *Por ser <math>a\,</math> la hipotenusa y <math>c\,</math> un cateto, tenemos que <math>c<a\,</math>. | *Por ser <math>a\,</math> la hipotenusa y <math>c\,</math> un cateto, tenemos que <math>c<a\,</math>. | ||
| }} | }} | ||
| + | |||
| ==Excentricidad de la elipse== | ==Excentricidad de la elipse== | ||
| ==Ecuación de la elipse== | ==Ecuación de la elipse== | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 19:26 30 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
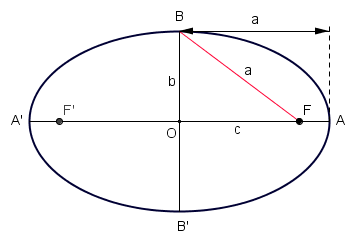
Elementos de la elipse
Dada una elipse de focos 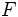 y y 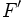 con ejes de simetría con ejes de simetría 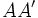 y y 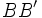 , que se cortan en el centro , que se cortan en el centro  de la elipse, determina los siguientes segmentos: de la elipse, determina los siguientes segmentos:
| 
|
Proposición
- La constante de la elipse es
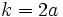 .
.
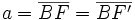
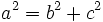
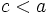
Demostración:
- La constante de la elipse es
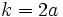 , pues
, pues
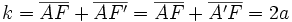
- Por ser
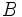 un punto de la elipse:
un punto de la elipse:
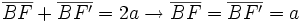
- Por el teorema de Pitágoras aplicado al triángulo
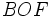 , tenemos
, tenemos
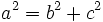
- Por ser
 la hipotenusa y
la hipotenusa y 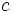 un cateto, tenemos que
un cateto, tenemos que 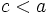 .
.
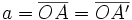 semieje mayor.
semieje mayor.
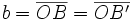 semieje menor.
semieje menor.
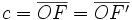 semidistancia focal.
semidistancia focal.

