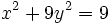La elipse (1ºBach)
De Wikipedia
| Revisión de 17:30 31 mar 2009 Coordinador (Discusión | contribuciones) (→Elementos de la elipse) ← Ir a diferencia anterior |
Revisión de 17:38 31 mar 2009 Coordinador (Discusión | contribuciones) (→Elementos de la elipse) Ir a siguiente diferencia → |
||
| Línea 43: | Línea 43: | ||
| {{AI2|titulo=Actividad interactiva: ''Propiedad de la elipse''|cuerpo= | {{AI2|titulo=Actividad interactiva: ''Propiedad de la elipse''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como se refleja un "rayo de luz" que parte de su foco, considerando que la elipse se comporta como un espejo. | + | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco. |
| |actividad= | |actividad= | ||
Revisión de 17:38 31 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
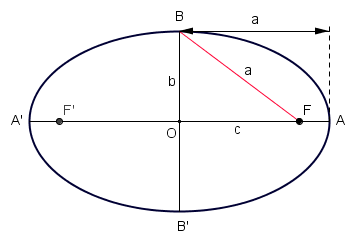
Elementos de la elipse
Una una elipse de focos
| 
|
|
Actividad interactiva: Propiedad de la elipse
Actividad 1: En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco.
Actividad: Ejercicios:
|
Excentricidad de la elipse
La escentricidad es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia.
La excentricidad de la elipse es el cociente entre la distancia focal y el eje mayor:
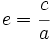
Propiedades
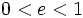 .
.
- Una elipse más se parece a a una circunferencia, cuanto más se aproxime a 0 su excentricidad.
- Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que

- y como
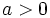 y
y  , tenemos que
, tenemos que 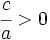
- Cuanto más próxima a 0 sea la excentricidad, más proximo a cero estará
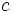 (la distancia focal se aproximará a cero) y
(la distancia focal se aproximará a cero) y  se aproximará a
se aproximará a  . Así, la elipse, se aproximará a una circunferencia de centro los focos y radio
. Así, la elipse, se aproximará a una circunferencia de centro los focos y radio 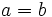 .
.
|
Actividad interactiva: Excentricidad de la elipse
Actividad 1: En la siguiente escena vamos a ver como se ve afectada la elipse si modificamos su excentricidad.
Actividad: Ejercicios:
|
Ecuaciones de la elipse
Ecuación reducida de la elipse
Ecuación reducida de la elipse
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y  los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
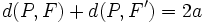
Sustituyendo las distancias por su fórmula matemática:
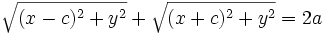
Pasamos la segunda raíz al segundo miembro:
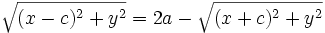
Se elevan al cuadrado ambos miebros y se simplifica:
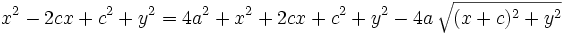
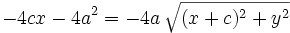
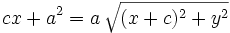
Se elevan al cuadrado los dos miembros:
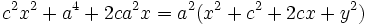
Reordenando y agrupando términos:
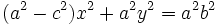
Teniendo en cuenta que 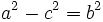 :
:
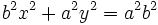
Dividiendo la expresión por 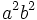 :
:
se obtiene la cuación buscada:
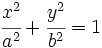
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9.
Actividad: La ecuación reducida viene dada por la fórmula: 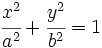 Sustituyendo a=5 y b=3, tenemos: 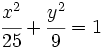 Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Ecuación de la elipse con los focos en el eje Y
Ecuación de la elipse con los focos en el eje Y
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
- Su excentricidad es:

Ecuación de la elipse con el centro desplazado del origen de coordenadas
Ecuación de la elipse con el centro desplazado del origen
- La ecuación de una elipse con semiejes
 y
y  y centro
y centro  es:
es:
|
|
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2.
Actividad: La ecuación reducida viene dada por la fórmula: 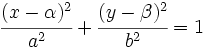 Sustituyendo  Puedes ver su gráfica en la siguente escena: Ejercicio:
|
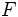 y
y 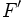 , con ejes de simetría
, con ejes de simetría 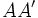 y
y 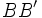 , que se cortan en el centro
, que se cortan en el centro  de la elipse, determina los siguientes segmentos:
de la elipse, determina los siguientes segmentos:
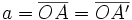
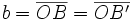
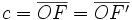
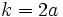 (constante de la elipse)
(constante de la elipse)
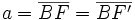
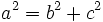
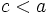
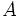 un punto de la elipse:
un punto de la elipse:
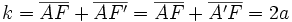
 un punto de la elipse:
un punto de la elipse:
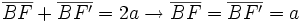
 , tenemos
, tenemos

 ,
, 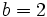 ,
, 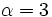 ,
,  , tenemos:
, tenemos: