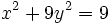La hipérbola (1ºBach)
De Wikipedia
| Revisión de 19:24 31 mar 2009 Coordinador (Discusión | contribuciones) (→Construcciones de la elipse) ← Ir a diferencia anterior |
Revisión de 19:28 31 mar 2009 Coordinador (Discusión | contribuciones) (→Construcciones de la hipérbola) Ir a siguiente diferencia → |
||
| Línea 226: | Línea 226: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' La elipse como envolvente (1). | + | |enunciado='''Actividad 2:''' La hipérbola como envolvente (1). |
| |actividad= | |actividad= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_6.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_2.html |
| width=780 | width=780 | ||
| height=460 | height=460 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_6.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_2.html '''Click''' aquí si no se ve bien la escena]</center> |
| - | Desliza el punto Q y observa. | + | Desliza el punto Q y observa los cambios. |
| - | *¿Qué cumple el segmento QR en cada momento respecto al punto F? | + | |
| - | Activa el trazo de QR y vuelve a deslizar el punto Q | + | |
| - | *¿Cuál es la envolvente de la familia de segmentos QR?, es decir, ¿cuál es la curva tangente a esa familia de segmentos? | + | |
| - | Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | + | |
| - | *¿De qué modo influye la posición relativa de F en la forma de la elipse generada? | + | |
| - | }} | + | Activa el trazo de la recta y vuelve a deslizar Q |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3:''' La elipse como envolvente (2). | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | *Aparece una hipérbola como la envolvente ¿de qué familia de rectas? |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_7.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_7.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa. La figura muestra por donde habría de doblarse la cicunferencia (si fuese de papel) para que el punto Q coincidiese con el F. | + | |
| - | + | ||
| - | Activa el trazo de la cuerda y vuelve a deslizar el punto Q | + | |
| - | *¿Cuál es la envolvente de la familia de esas cuerdas?, es decir, ¿cuál es la curva tangente a esa familia de segmentos? | + | |
| Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | ||
| - | *¿De qué modo influye la posición relativa de F en la forma de la elipse generada? | ||
| - | }} | + | *¿De qué modo influye la posición relativa de F en la forma de la cónica generada? |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 4:''' La elipse a partir de dos circunferencias. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_8.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_8.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa. | + | |
| - | + | ||
| - | *¿Cómo está determinado el punto P? | + | |
| - | + | ||
| - | Activa su trazo y vuelve a deslizar el punto Q. | + | |
| }} | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 5:''' La elipse como hipotrocoide. | ||
| - | |actividad= | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_9.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_9.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Desliza el punto verde y observa. | ||
| - | |||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 6:''' La elipse mediante el compás de [[Arquímedes]]. | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_10.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_10.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Al utilizar el deslizador comprobarás el movimiento de un segmento de longitud fija cuyos extremos se deslizan sobre dos ejes perpendiculares. | ||
| - | |||
| - | *¿Qué trayectoria describirá un punto determinado de ese segmento? | ||
| - | |||
| - | Activa el trazo de P para comprobarlo. | ||
| - | |||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 7:''' La elipse a partir de dos circunferencias tangentes interiores. | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_11.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_11.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Desliza el punto Q y observa. | ||
| - | |||
| - | Activa el trazo del centro de la circunferencia interior y vuelve a deslizar el punto Q. | ||
| - | |||
| - | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 19:28 31 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Elementos de la hipérbola
Excentricidad de la hipérbola
La excentricidad es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia.
La excentricidad de la hipérbola es el cociente entre la distancia focal y el eje:
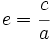
Propiedades
- En una hipérbola
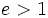 .
.
- Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que
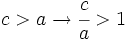
|
Actividad interactiva: Excentricidad de la hipérbola
Actividad 1: En la siguiente escena vamos a ver como se ve afectada la hipérbola si modificamos su excentricidad.
Actividad: Ejercicios: Modifica el valor de e (deslizando el punto verde) y observa los cambios.
Pulsa el botón Actualizar para recuperar la imagen inicial. Modifica el valor de a y observa los cambios.
|
Ecuaciones de la elipse
Ecuación reducida de la elipse
Ecuación reducida de la elipse
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y  los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
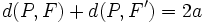
Sustituyendo las distancias por su fórmula matemática:
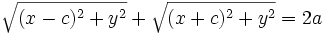
Pasamos la segunda raíz al segundo miembro:
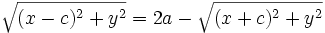
Se elevan al cuadrado ambos miebros y se simplifica:
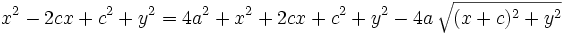
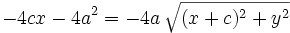
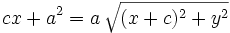
Se elevan al cuadrado los dos miembros:
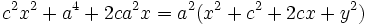
Reordenando y agrupando términos:
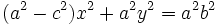
Teniendo en cuenta que 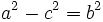 :
:
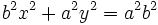
Dividiendo la expresión por 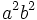 :
:
se obtiene la cuación buscada:
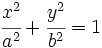
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9.
Actividad: La ecuación reducida viene dada por la fórmula: 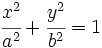 Sustituyendo a=5 y b=3, tenemos: 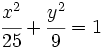 Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Ecuación de la elipse con los focos en el eje Y
Ecuación de la elipse con los focos en el eje Y
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
- Su excentricidad es:

Ecuación de la elipse con el centro desplazado del origen de coordenadas
Ecuación de la elipse con el centro desplazado del origen
- La ecuación de una elipse con semiejes
 y
y  y centro
y centro 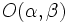 es:
es:
|
|
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2.
Actividad: La ecuación reducida viene dada por la fórmula: 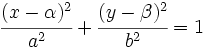 Sustituyendo  Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Construcciones de la hipérbola
|
Actividad interactiva: Construcciones de la elipse
Actividad 1: Usando la definición de hipérbola como lugar geométrico.
Actividad: En la siguiente escena, activa la traza, desliza el punto P y observa.
Actividad 2: La hipérbola como envolvente (1).
Actividad: Desliza el punto Q y observa los cambios. Activa el trazo de la recta y vuelve a deslizar Q
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior.
|
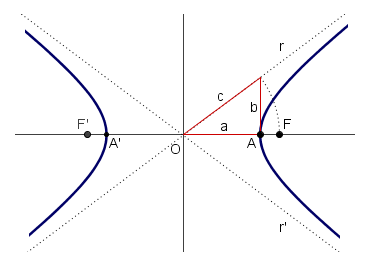
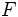 y
y 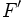 , con asíntotas
, con asíntotas  y
y 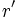 , con ejes de simetría
, con ejes de simetría 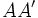 y su perpendicular pasando por su centro
y su perpendicular pasando por su centro  , determina los siguientes segmentos:
, determina los siguientes segmentos:
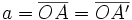
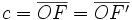
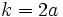 (constante de la hipérbola)
(constante de la hipérbola)
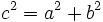

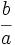 y
y 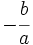 .
.
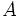 un punto de la hipérbola:
un punto de la hipérbola:
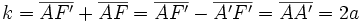
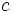 , tenemos
, tenemos
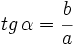

 ,
, 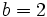 ,
, 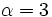 ,
,  , tenemos:
, tenemos: