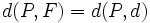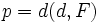La parábola (1ºBach)
De Wikipedia
| Revisión de 19:31 1 abr 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:32 1 abr 2009 Coordinador (Discusión | contribuciones) (→Elementos de la parábola) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| *{{Sube|porcentaje=+10%|contenido=<math>O\,</math>}} '''(vértice)'''. | *{{Sube|porcentaje=+10%|contenido=<math>O\,</math>}} '''(vértice)'''. | ||
| *{{Sube|porcentaje=+10%|contenido=<math>p=d(d,F)\,</math>}} '''(distancia del foco a la directriz)'''. | *{{Sube|porcentaje=+10%|contenido=<math>p=d(d,F)\,</math>}} '''(distancia del foco a la directriz)'''. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 65: | Línea 66: | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| ==Excentricidad de la parábola== | ==Excentricidad de la parábola== | ||
| {{Caja Amarilla|texto=La excentricidad de la parábola es el cociente entre <math>c=d(F,O)\,</math> y <math>a=d(O,d)\,</math>. En consecuencia, la excentricidad de la parábola es siempre igual a 1. | {{Caja Amarilla|texto=La excentricidad de la parábola es el cociente entre <math>c=d(F,O)\,</math> y <math>a=d(O,d)\,</math>. En consecuencia, la excentricidad de la parábola es siempre igual a 1. | ||
Revisión de 19:32 1 abr 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
La parábola
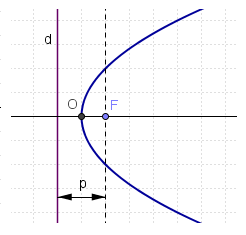
Dados un punto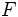 
llamado foco, y una recta 
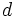, llamada directriz, se llama parábola al lugar geométrico de los puntos 
del plano que equidistán del foco y de la directriz:
|
|
Elementos de la parábola
Una parábola de foco
| 
|
 Actividad interactiva: Propiedades de la parábola
Actividad 1: En la siguiente escena vamos a ver una propiedad de la parábola en la que veremos como cualquier "rayo" perpendicular a la directriz que impacte en la curva se refleja y va a parar a su foco.
Actividad:
Desliza el punto verde hacia la derecha y observa:
Actividad 2: Tiro parabólico
Actividad:
En la figura se puede observar la trayectoria de un proyectil (cuya velocidad de salida es constante). Prueba a modificar el ángulo de inclinación inicial.
Activa el trazo de para comprobar la zona de alcance de los proyectiles.
|
Excentricidad de la parábola
La excentricidad de la parábola es el cociente entre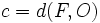 
y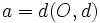 
. En consecuencia, la excentricidad de la parábola es siempre igual a 1.
Construcciones de la parábola
Actividad interactiva: Construcciones de la parábola
Actividad 1: Método basado en su definición como lugar geométrico.
Actividad: Activa la traza, desliza el punto P y observa.
Actividad 2: La parábola como envolvente.
Actividad: Desliza el punto P y observa. Activa el trazo de la perpendicular a PF por P y vuelve a deslizar el punto P
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F o de la recta directriz y repite lo anterior.
Actividad 3: La parábola generada por el centro de una circunferencia.
Actividad: Desliza el punto P y observa.
Activa el trazo del centro de la circunferencia y vuelve a deslizar el punto P.
|
