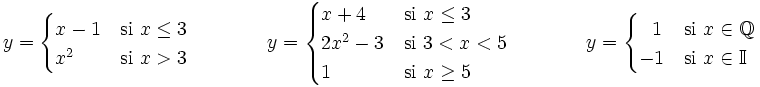Plantilla:Funciones definidas a trozos
De Wikipedia
| Revisión de 19:21 17 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:45 17 abr 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 75: | Línea 75: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://maralboran.org/web_ma/descartes/Analisis/funcion_a_trozos/funcion_a_trozos3_1.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/Analisis/funcion_a_trozos/funcion_a_trozos3_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2.''' Representación gráfica de distintas funciones definidas a trozos (dos trozos). | ||
| + | |actividad= | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/geogebra/figuras/ftrozos__1.html | ||
| + | widfth=780 | ||
| + | height=460 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/f_trozos_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 07:45 17 abr 2009
Una función definida a trozos es aquella que utiliza varias expresiones para su definición, utilizando cada una de ellas en un determinado tramo del dominio de definición de la función principal.
Son funciones definidas a trozos:
 Actividad Interactiva: Funciones definidas a trozos
Actividad 1: Ejemplo de función definida a trozos.
Actividad: En la siguiente escena puedes ver la representación de la función  Mueve el punto P para ver que expresión corresponde a cada tramo.
Actividad 2: El entrenamiento y otros ejemplos de funciones a trozos.
Actividad 3: Une cada función con su gráfica.
|
Ejemplo: Función definida a trozos
Representa la siguiente función:
Para su representación, tenemos que dibujar cada una de las tres funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición).
Actividad Interactiva: Funciones definidas a trozos
Actividad 1: Funciones lineales definidas en dos trozos.
Actividad: En esta escena representaremos funciones a trozos del tipo:  Modifica con los controles los valores de a, b, c, d y k. Podrás obtener así distintas funciones a trozos.
Actividad 2. Representación gráfica de distintas funciones definidas a trozos (dos trozos).
|
