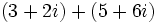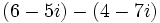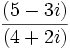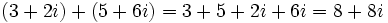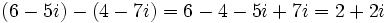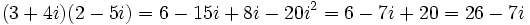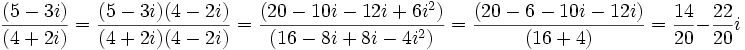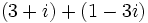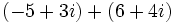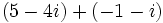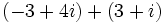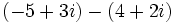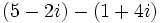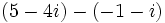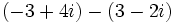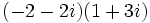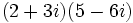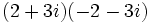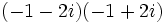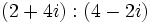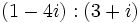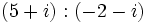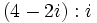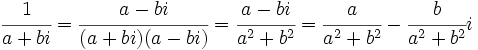Números complejos: Operaciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:14 11 mar 2009 Coordinador (Discusión | contribuciones) (→Propiedades de las operaciones con números complejos) ← Ir a diferencia anterior |
Revisión de 06:41 21 abr 2009 Coordinador (Discusión | contribuciones) (→Operaciones con números complejos en forma binómica) Ir a siguiente diferencia → |
||
| Línea 30: | Línea 30: | ||
| {{AI2|titulo=Actividad interactiva: ''Operaciones con números complejos''|cuerpo= | {{AI2|titulo=Actividad interactiva: ''Operaciones con números complejos''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=:'''Actividad 3:''' Efectúa las siguientes operaciones en tu cuaderno y haz una comprobación posterior en la escena: | + | |enunciado=:'''Actividad 1:''' Efectúa las siguientes sumas de números complejos en tu cuaderno y haz una comprobación posterior en la escena: |
| :# <math>\,(3 + i) + (1 - 3i)</math> | :# <math>\,(3 + i) + (1 - 3i)</math> | ||
| - | :# <math>\,(-5 + 3i) - (6 + 4i)</math> | + | :# <math>\,(-5 + 3i) + (6 + 4i)</math> |
| :# <math>\,(5 - 4i) + (-1 - i)</math> | :# <math>\,(5 - 4i) + (-1 - i)</math> | ||
| - | :# <math>\,(-3 + 4i)-(3 + i)</math> | + | :# <math>\,(-3 + 4i)+(3 + i)</math> |
| {{p}} | {{p}} | ||
| |actividad= | |actividad= | ||
| - | En esta escena tienes representados los números complejos: z1=a+bi y z2=c+di | + | Utiliza el deslizador verde para comprobar cómo se obtiene la suma de dos complejos por el "método del paralelogramo" |
| - | Así como su SUMA z1+z2 y su RESTA z1-z2 (Recuerda el paralelogramo que se forma con dos vectores, cuyas diagonales son la suma y la resta de los mismos, fíjate bien en la escena) | + | Mueve los puntos azules para modificar los datos. |
| - | Puedes cambiar los valores de a, b, c y d, moviendo los AFIJOS de z1 y/o z2 con el ratón, o bien introduciendo sus valores en la parte inferior de la escena. | ||
| - | Observa la escena y averigua cómo se SUMAN y se RESTAN números complejos. | + | <center><iframe> |
| + | url=http://maralboran.org/web_ma/geogebra/figuras/complejos_suma.html | ||
| + | width=780 | ||
| + | height=460 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_suma.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=:'''Actividad 1:''' Efectúa las siguientes restas de números complejos en tu cuaderno y haz una comprobación posterior en la escena: | ||
| + | |||
| + | :# <math>\,(-5 + 3i) - (4 + 2i)</math> | ||
| + | :# <math>\,(5 -2i) -(1+ 4i)</math> | ||
| + | :# <math>\,(5 - 4i) - (-1 - i)</math> | ||
| + | :# <math>\,(-3 + 4i)-(3 - 2i)</math> | ||
| + | {{p}} | ||
| + | |actividad= | ||
| + | Utiliza el deslizador verde para comprobar cómo se obtiene la resta de dos complejos por el "método del paralelogramo" | ||
| + | |||
| + | Mueve los puntos azules para modificar los datos. | ||
| + | |||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_1.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/complejos_resta1.html |
| - | width=430 | + | width=780 |
| - | height=390 | + | height=460 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_resta1.html '''Click''' aquí si no se ve bien la escena]</center> |
| + | |||
| + | |||
| + | Otro modo de restar números complejos es sumar el opuesto: puedes comprobarlo en la siguiente figura: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/geogebra/figuras/complejos_resta2.html | ||
| + | width=780 | ||
| + | height=460 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_resta2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=:'''Actividad 2:''' Efectúa las siguientes multiplicaciones en tu cuaderno y haz una comprobación posterior en la escena: | + | |enunciado=:'''Actividad 3:''' Efectúa las siguientes multiplicaciones en tu cuaderno y haz una comprobación posterior en la escena: |
| :# <math>\,(-2 -2i) (1 + 3i)</math> | :# <math>\,(-2 -2i) (1 + 3i)</math> | ||
| Línea 63: | Línea 94: | ||
| :# <math>\,(-1-2i)(-1+2i)</math> | :# <math>\,(-1-2i)(-1+2i)</math> | ||
| {{p}} | {{p}} | ||
| - | |actividad= | + | |actividad=Utiliza el deslizador verde para comprobar cómo se obtiene el producto de dos complejos, a partir del triángulo construido a partir del primer número complejo, el origen de coordenadas y el punto (1,0). |
| - | En la escena adjunta se muestra la forma de realizar el producto de dos números complejos, z1·z2=(a+bi)(c+di) | + | |
| - | + | Mueve los puntos azules para modificar los datos. | |
| - | Moviendo los AFIJOS de z1 y z2, o introduciendo los valores de a, b, c y d, puedes ir viendo los resultados. | + | |
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_2.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/complejos_prod.html |
| - | width=430 | + | width=780 |
| - | height=390 | + | height=460 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_prod.html '''Click''' aquí si no se ve bien la escena]</center> |
| + | |||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=:'''Actividad 3:''' Efectúa las siguientes divisiones en tu cuaderno y compruébalas en la escena: | + | |enunciado=:'''Actividad 4:''' Efectúa las siguientes divisiones en tu cuaderno y compruébalas en la escena: |
| :# <math>\,(2+4i):(4-2i)</math> | :# <math>\,(2+4i):(4-2i)</math> | ||
| Línea 85: | Línea 117: | ||
| {{p}} | {{p}} | ||
| |actividad= | |actividad= | ||
| - | En la escena adjunta se muestra la forma de realizar el cociente de dos números complejos, z1:z2=(a+bi):(c+di) | + | Utiliza el deslizador verde para comprobar cómo se obtiene el cociente de dos complejos, a partir del triángulo construido a partir de los dos. |
| - | Puedes cambiar los valores de a, b, c y d, o mover los puntos z1 y z2 para hallar otras divisiones. | + | |
| + | Mueve los puntos azules para modificar los datos. | ||
| + | |||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_3.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/complejos_div.html |
| - | width=430 | + | width=780 |
| - | height=390 | + | height=460 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos3_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_div.html '''Click''' aquí si no se ve bien la escena]</center> |
| - | + | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 06:41 21 abr 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Operaciones con números complejos en forma binómica
- Suma:
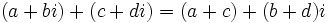
- Resta:
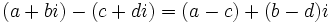
- Multiplicación:
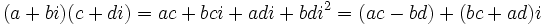
- División:
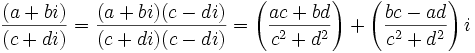 , siempre que
, siempre que 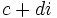 no sea nulo.
no sea nulo.
|
Actividad interactiva: Operaciones con números complejos
Actividad: Utiliza el deslizador verde para comprobar cómo se obtiene la suma de dos complejos por el "método del paralelogramo" Mueve los puntos azules para modificar los datos.
Actividad: Utiliza el deslizador verde para comprobar cómo se obtiene la resta de dos complejos por el "método del paralelogramo" Mueve los puntos azules para modificar los datos.
Actividad: Utiliza el deslizador verde para comprobar cómo se obtiene el producto de dos complejos, a partir del triángulo construido a partir del primer número complejo, el origen de coordenadas y el punto (1,0). Mueve los puntos azules para modificar los datos.
Actividad: Utiliza el deslizador verde para comprobar cómo se obtiene el cociente de dos complejos, a partir del triángulo construido a partir de los dos. Mueve los puntos azules para modificar los datos.
|
Propiedades de las operaciones con números complejos
- El 0 es el elemento neutro de la suma.
- Todo número complejo,
 , tiene un opuesto,
, tiene un opuesto, 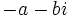
- El 1 es el elemento neutro del producto.
- Todo número complejo,
 , distinto de 0, tiene inverso,
, distinto de 0, tiene inverso, 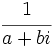 :
: