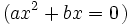Plantilla:Ecuaciones de segundo grado incompletas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 00:49 15 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:43 27 ene 2010 Coordinador (Discusión | contribuciones) (→Ecuaciones de segundo grado incompletas) Ir a siguiente diferencia → |
||
| Línea 4: | Línea 4: | ||
| *<math>b=0\;\!</math>: <math>(ax^2+c=0\;\!)</math> | *<math>b=0\;\!</math>: <math>(ax^2+c=0\;\!)</math> | ||
| :En este caso las soluciones se obtienen despejando x: | :En este caso las soluciones se obtienen despejando x: | ||
| - | <center><math>ax^2+c=0; \quad ax^2=-c; \quad x=-\cfrac{c}{a};\quad x=\pm \sqrt {-\cfrac{c}{a}}</math></center> | + | <center><math>ax^2+c=0; \quad ax^2=-c; \quad x^2=-\cfrac{c}{a};\quad x=\pm \sqrt {-\cfrac{c}{a}}</math></center> |
| *<math>c=0\;\!</math>: <math>(ax^2+bx=0\;\!)</math> | *<math>c=0\;\!</math>: <math>(ax^2+bx=0\;\!)</math> | ||
| :En este caso, sacando factor común e igualando a cero cada factor: | :En este caso, sacando factor común e igualando a cero cada factor: | ||
Revisión de 07:43 27 ene 2010
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado 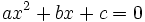 es incompleta, si ocurre uno de los siguientes casos:
es incompleta, si ocurre uno de los siguientes casos:
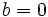 :
: 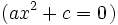
- En este caso las soluciones se obtienen despejando x:
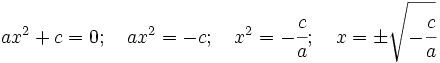
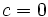 :
: 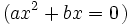
- En este caso, sacando factor común e igualando a cero cada factor:
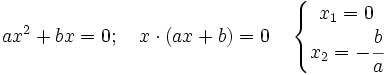
Ejemplo: Ecuaciones de segundo grado incompletas
- Ejemplos de ecuaciones de segundo grado incompletas resueltas.
Solución:
Pulsa "INICIO" para ver otros ejemplos:
- Caso 1:
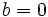 :
: 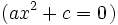
- Caso 2:
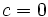 :
: