Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
| Revisión de 08:27 28 sep 2014 Coordinador (Discusión | contribuciones) (→Razones trigonométricas) ← Ir a diferencia anterior |
Revisión de 12:07 28 sep 2014 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de los ángulos más famosos) Ir a siguiente diferencia → |
||
| Línea 172: | Línea 172: | ||
| ==Razones trigonométricas de los ángulos más famosos== | ==Razones trigonométricas de los ángulos más famosos== | ||
| + | ==Razones trigonométricas de algunos ángulos importantes== | ||
| + | A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar: | ||
| + | {{p}} | ||
| + | {| {{tablabonita_blanca}} | ||
| + | |-style="background:#e1ecf7;" align="center" | ||
| + | ! '''Radianes''' | ||
| + | ! '''Grados''' | ||
| + | ! sen | ||
| + | ! cos | ||
| + | ! tg | ||
| + | ! cosec | ||
| + | ! sec | ||
| + | ! cot | ||
| + | |----- | ||
| + | | align="center" | <math> 0 \; </math> | ||
| + | | align="center" | <math>0^o \,</math> | ||
| + | | align="center" | <math>0 \;</math> | ||
| + | | align="center" | <math>1 \;</math> | ||
| + | | align="center" | <math>0 \;</math> | ||
| + | | align="center" | <math>\not{\exists} \,\!</math> | ||
| + | | align="center" | <math>1 \;</math> | ||
| + | | align="center" | <math>\not{\exists} \,\!</math> | ||
| + | |----- | ||
| + | | align="center" | <math> \frac{\pi}{6} </math> | ||
| + | | align="center" | <math>30^o \,</math> | ||
| + | | align="center" | <math>\frac{1}{2}</math> | ||
| + | | align="center" | <math>\frac{\sqrt{3}}{2}</math> | ||
| + | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | ||
| + | | align="center" | <math>2 \,</math> | ||
| + | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | ||
| + | | align="center" | <math>\sqrt{3}</math> | ||
| + | |----- | ||
| + | | align="center" | <math> \frac{\pi}{4} </math> | ||
| + | | align="center" | <math>45^o \,</math> | ||
| + | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | ||
| + | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | ||
| + | | align="center" | <math>1 \,</math> | ||
| + | | align="center" | <math>\sqrt{2}</math> | ||
| + | | align="center" | <math>\sqrt{2}</math> | ||
| + | | align="center" | <math>1 \,</math> | ||
| + | |----- | ||
| + | | align="center" | <math> \frac{\pi}{3} </math> | ||
| + | | align="center" | <math>60^o \,</math> | ||
| + | | <math>\frac{\sqrt{3}}{2}</math> | ||
| + | | align="center" | <math>\frac{1}{2}</math> | ||
| + | | align="center" | <math>\sqrt{3}</math> | ||
| + | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | ||
| + | | align="center" | <math>2 \,</math> | ||
| + | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | ||
| + | |----- | ||
| + | | align="center" | <math> \frac{\pi}{2}</math> | ||
| + | | align="center" | <math>90^o \,</math> | ||
| + | | align="center" | <math>1 \;</math> | ||
| + | | align="center" | <math>0 \;</math> | ||
| + | | align="center" | <math>\not{\exists} \,\!</math> | ||
| + | | align="center" | <math>1 \,</math> | ||
| + | | align="center" | <math>\not{\exists} \,\!</math> | ||
| + | | align="center" | <math>0 \,</math> | ||
| + | |} | ||
| + | {{p}} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| |titulo1=Razones trigonométricas de ángulos complementarios | |titulo1=Razones trigonométricas de ángulos complementarios | ||
| Línea 186: | Línea 246: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Calculadora== | ==Calculadora== | ||
| ===Funciones trigonométricas (directas)=== | ===Funciones trigonométricas (directas)=== | ||
Revisión de 12:07 28 sep 2014
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Razones trigonométricas de un ángulo agudo
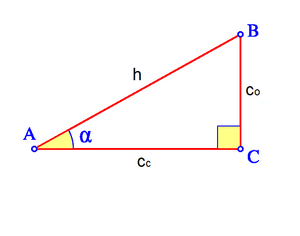
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo agudo  , de la siguiente manera:
, de la siguiente manera:
|
Razones trigonométricas recíprocas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón recíproca del seno:
- La secante (abreviado como sec), razón recíproca del coseno:
- La cotangente (abreviado como cot), razón recíproca de la tangente:
Videotutoriales
- Razones trigonométricas de un ángulo agudo.
- Razones trigonométricas recíprocas.
- Ejemplos.
Videotutorial
Videotutorial
Videotutorial
- Definición razonada de las razones trigonométricas de un ángulo agudo.
|
Actividad interactiva: Razones trigonométricas
Actividad 1: Practica con las razones trigonométricas y ponte a prueba con una autoevaluación
Actividad:
|
Relaciones fundamentales de la trigonometría
Relaciones fundamentales de la trigonometría
- 1.
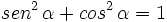
- 2.

- 3.
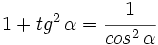
1. 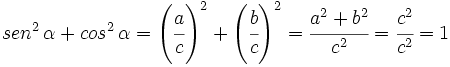
ya que, por el teorema de Pitágoras, 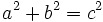 .
.
2. 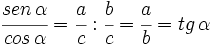
3. 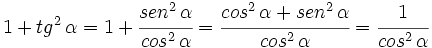
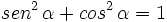
Videotutoriales
Videotutorial
Videotutorial
Ejercicios
|
Ejercicios: Relaciones fundamentales de la trigonometría
1. Sabiendo que
 , calcula , calcula 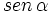 y y 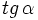 . .Solución: 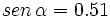
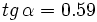
2. Sabiendo que
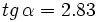 , calcula , calcula 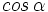 y y 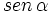 Solución: 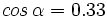
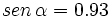 |
Razones trigonométricas de los ángulos más famosos
Razones trigonométricas de algunos ángulos importantes
A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar:
| Radianes | Grados | sen | cos | tg | cosec | sec | cot |
|---|---|---|---|---|---|---|---|
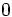
| 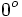
| 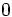
| 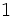
| 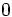
| 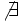
| 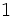
| 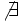
|
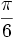
| 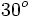
| 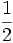
| 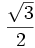
| 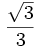
| 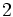
| 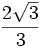
| 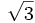
|
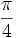
| 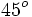
| 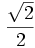
| 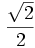
| 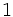
| 
| 
| 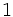
|
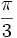
| 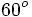
| 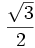
| 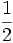
| 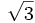
| 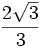
| 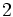
| 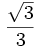
|
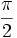
| 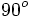
| 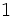
| 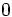
| 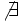
| 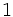
| 
| 
|
Videotutorial
Videotutorial
Calculadora
Funciones trigonométricas (directas)
Seno
|
Calculadora: Seno |
Coseno
|
Calculadora: Coseno |
Tangente
|
Calculadora: Tangente |
Funciones trigonométricas (inversas)
Aco seno
|
Calculadora: Arco seno Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre -90º y 90º). Hay otra solución en el segundo o tercer cuadrante que se obtiene restando a 180º la solución obtenida. En este ejemplo, la otra solución sería 180º-30º=150º. |
Arco coseno
|
Calculadora: Arco coseno Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre 0º y 180º). Hay otra solución en el tercer o cuarto cuadrante que se obtiene restando a 360º la solución obtenida. En este ejemplo, la otra solución sería 360º-60º=300º. |
Arco tangente
|
Calculadora: Arco tangente Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre -90º y 90º). Hay otra solución en el segundo o tercer cuadrante que se obtiene sumando 180º a la solución obtenida. En este ejemplo, la otra solución sería 180º+45º=225º. |
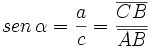
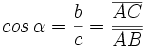
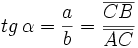
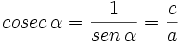
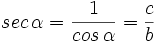
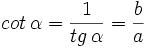
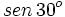
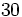
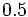
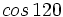
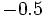
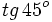
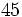
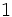
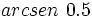
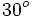 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).
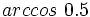
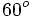 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).
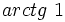
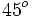 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).

