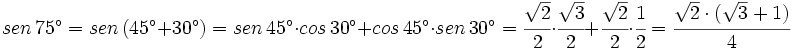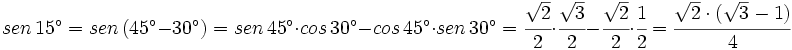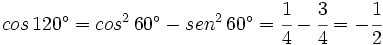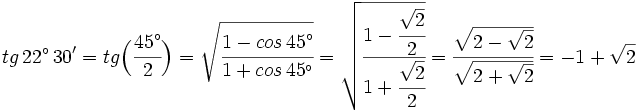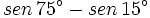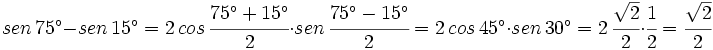Fórmulas trigonométricas (1ºBach)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 17:03 30 sep 2014

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

Tabla de contenidos

1 Razones trigonométricas de la suma de dos ángulos
2 Razones trigonométricas de la diferencia de dos ángulos
3 Razones trigonométricas del ángulo doble
4 Razones trigonométricas del ángulo mitad
5 Transformaciones de sumas y diferencias de senos y cosenos en productos

Razones trigonométricas de la suma de dos ángulos

Razones trigonométricas de la suma de dos ángulos

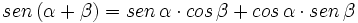
I.1: $sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + cos \, \alpha \cdot sen \, \beta$

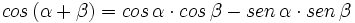
I.2: $cos \, (\alpha + \beta) = cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta$

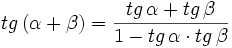
I.3: $tg \, (\alpha + \beta) = \frac{tg \, \alpha + tg \, \beta}{1 - tg \, \alpha \cdot tg \, \beta}$

Demostración:

I.1:

$sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}$

En el triángulo ABC: $\overline{CA}=\overline{AB} \cdot cos \, \alpha$
En el triángulo OAQ: $\overline{AQ}=\overline{OA} \cdot sen \, \alpha$
En el triángulo OBA: $\begin{cases} \overline{AB}=\overline{OB} \cdot sen \, \beta \\ \overline{OA}=\overline{OB} \cdot cos \, \beta \end{cases}$

Sustituyendo:

$sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}=\cfrac{\overline{AB} \cdot cos \, \alpha +\overline{OA} \cdot sen \, \alpha}{\overline{OB}}=$

$=\cfrac{\overline{OB} \cdot sen \, \beta \cdot cos \, \alpha +\overline{OB} \cdot cos \, \beta \cdot sen \, \alpha}{\overline{OB}}=$

$= sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha$

I.2:

$cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}$

En el triángulo ABC: $\overline{BC}=\overline{AB} \cdot sen \, \alpha$
En el triángulo OAQ: $\overline{OQ}=\overline{OA} \cdot cos \, \alpha$

Sustituyendo:

$cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}=\cfrac{\overline{OA} \cdot cos \, \alpha -\overline{AB} \cdot sen \, \alpha}{\overline{OB}}=$

$\cfrac{\overline{OB} \cdot cos \, \beta \cdot cos \, \alpha -\overline{OB} \cdot sen \, \beta \cdot sen \, \alpha}{\overline{OB}}=$

$= cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta$

I.3:

$tg \, (\alpha + \beta)=\cfrac{sen \, (\alpha + \beta)}{cos \, (\alpha + \beta)}=\cfrac{sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta}=$

(Dividiendo numerador y denominador por $cos \, \alpha \cdot \cos \, \beta$ )

$=\cfrac{\cfrac{sen \, \beta \cdot cos \, \alpha}{cos \, \alpha \cdot \cos \, \beta} + \cfrac{cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot \cos \, \beta}}{\cfrac{cos \, \alpha \cdot cos \, \beta}{cos \, \alpha \cdot \cos \, \beta} - \cfrac{sen \, \alpha \cdot sen \, \beta}{cos \, \alpha \cdot \cos \, \beta}}=\cfrac{tg \, \beta + tg \, \alpha}{1-tg \, \alpha \cdot tg \, \beta}$

Razones trigonométricas de la suma de dos ángulos (12´41) Sinopsis:

Videotutorial.

Ejemplo: Razones trigonométricas de la suma de dos ángulos

Calcula el valor exacto de 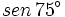$sen \, 75^\circ \,$ (sin calculadora)

Solución:

$sen \, 75^\circ= sen \, (45^\circ + 30^\circ)=sen \, 45^\circ \cdot cos \, 30^\circ + cos \, 45^\circ \cdot sen \, 30^\circ= \cfrac{\sqrt{2}}{2} \cdot \cfrac{\sqrt{3}}{2}+ \cfrac{\sqrt{2}}{2} \cdot \cfrac{1}{2}=\cfrac{\sqrt{2} \cdot (\sqrt{3}+1)}{4}$

Ejercicios

3 ejercicios (5´23") Sinopsis:

Seno, coseno y tangente de la suma de tres ángulos.

Razones trigonométricas de la diferencia de dos ángulos

Razones trigonométricas de la diferencia de dos ángulos

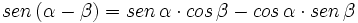
II.1: $sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta$

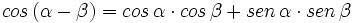
II.2: $cos \, (\alpha - \beta) = cos \, \alpha \cdot cos \, \beta + sen \, \alpha \cdot sen \, \beta$

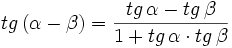
II.3: $tg \, (\alpha - \beta) = \frac{tg \, \alpha - tg \, \beta}{1 + tg \, \alpha \cdot tg \, \beta}$

Demostración:

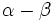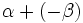Para las demostraciones basta sustituir $\alpha - \beta \,$ por $\alpha + (-\beta) \,$ y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:

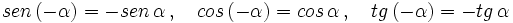
$sen \, (-\alpha)=-sen \, \alpha \, , \quad cos \, (-\alpha)=cos \, \alpha \, , \quad tg \, (-\alpha)=-tg \, \alpha$

Ejemplo: Razones trigonométricas de la diferencia de dos ángulos

Calcula el valor exacto de 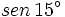$sen \, 15^\circ$ (sin calculadora)

Solución:

$sen \, 15^\circ= sen \, (45^\circ - 30^\circ)=sen \, 45^\circ \cdot cos \, 30^\circ - cos \, 45^\circ \cdot sen \, 30^\circ= \cfrac{\sqrt{2}}{2} \cdot \cfrac{\sqrt{3}}{2}- \cfrac{\sqrt{2}}{2} \cdot \cfrac{1}{2}=\cfrac{\sqrt{2} \cdot (\sqrt{3}-1)}{4}$

Razones trigonométricas del ángulo doble

Razones trigonométricas del ángulo doble

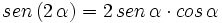
III.1: $sen \, (2 \, \alpha) = 2 \, sen \, \alpha \cdot cos \, \alpha$

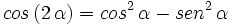
III.2: $cos \, (2 \, \alpha) = cos^2 \, \alpha - sen^2 \, \alpha$

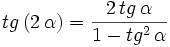
III.3: $tg \, (2 \, \alpha) = \frac{2 \, tg \, \alpha}{1 - tg^2 \, \alpha}$

Demostración:

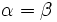Basta utilizar las fórmulas de la suma (I.1, I.2 y I.3) y hacer $\alpha= \beta \,$ .

Ejemplo: Razones trigonométricas del ángulo doble

Calcula el valor de 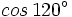$cos \, 120^\circ \,$ a partir de las razones trigonométricas de 60º.

Solución:

$cos \, 120^\circ= cos^2 \, 60^\circ - sen^2 \, 60^\circ=\cfrac{1}{4}-\cfrac{3}{4}=-\cfrac{1}{2}$

Razones trigonométricas del ángulo mitad

Razones trigonométricas del ángulo mitad

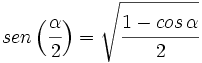
IV.1: $sen \, \Big( \cfrac{\alpha}{2} \Big) = \sqrt{\cfrac{1-cos \, \alpha}{2}}$

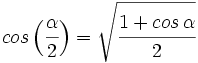
IV.2: $cos \, \Big( \cfrac{\alpha}{2} \Big) = \sqrt{\cfrac{1+cos \, \alpha}{2}}$

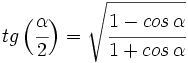
IV.3: $tg \, \Big( \cfrac{\alpha}{2} \Big) = \sqrt{\cfrac{1-cos \, \alpha}{1+cos \, \alpha}}$

Demostración:

Teniendo en cuenta que 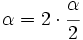$\alpha= 2 \cdot \cfrac{\alpha}{2}$ y utilizando la fórmula III.2 del coseno del ángulo doble, tenemos:

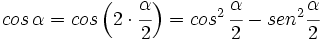
$cos \, \alpha=cos \, \Big( 2 \cdot \cfrac{\alpha}{2} \Big) = cos^2 \, \cfrac{\alpha}{2}- sen^2 \cfrac{\alpha}{2}$

que combinado con la fórmula fundamental, nos da el siguiente sistema:

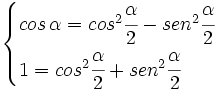
$\begin{cases} cos \, \alpha = cos^2 \cfrac{\alpha}{2} - sen^2 \cfrac{\alpha}{2} \\ 1= cos^2 \cfrac{\alpha}{2} + sen^2 \cfrac{\alpha}{2} \end{cases}$

Sumando y restando ambas ecuaciones, tenemos las siguientes expresiones:

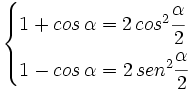
$\begin{cases} 1 + cos \, \alpha = 2 \, cos^2 \cfrac{\alpha}{2} \\ 1 - cos \, \alpha = 2 \, sen^2 \cfrac{\alpha}{2}\end{cases}$

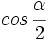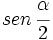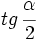De estas igualdades se despejan $cos \, \cfrac{\alpha}{2}$ y $sen \, \cfrac{\alpha}{2}$ , y a partir de ellos, se obtiene el valor de $tg \, \cfrac{\alpha}{2}$ .

Ejemplo: Razones trigonométricas del ángulo mitad

Calcula el valor exacto de 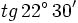$tg \, 22^\circ \, 30'$ (sin calculadora).

Solución:

$tg \, 22^\circ \, 30'= tg \Big( \cfrac{45^\circ}{2} \Big)=\sqrt{\cfrac{1-cos \, 45^\circ}{1+cos \, 45^\circ}}=\sqrt{\cfrac{1-\cfrac{\sqrt{2}}{2}}{1+\cfrac{\sqrt{2}}{2}}}=\cfrac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}=-1+\sqrt{2}$

Transformaciones de sumas y diferencias de senos y cosenos en productos

Transformaciones de sumas en productos

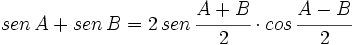
V.1: $sen \, A + sen \, B = 2 \, sen \, \cfrac{A+B}{2} \cdot cos \, \cfrac{A-B}{2}$

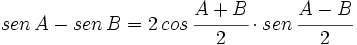
V.2: $sen \, A - sen \, B = 2 \, cos \, \cfrac{A+B}{2} \cdot sen \, \cfrac{A-B}{2}$

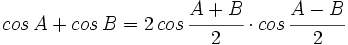
V.3: $cos \, A + cos \, B = 2 \, cos \, \cfrac{A+B}{2} \cdot cos \, \cfrac{A-B}{2}$

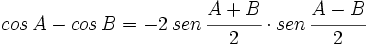
V.4: $cos \, A - cos \, B = -2 \, sen \, \cfrac{A+B}{2} \cdot sen \, \cfrac{A-B}{2}$

Demostración:

V.1 y V.2:

Partiendo de las expresiones del I.1 y II.1 del seno de una suma y de una diferencia:

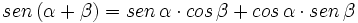
I.1: $sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + cos \, \alpha \cdot sen \, \beta$

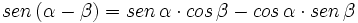
II.1: $sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta$

Sumando y restando ambas expresiones, obtenemos:

Sumando: $sen \, (\alpha + \beta) +sen \, (\alpha - \beta)= 2 \, sen \, \alpha \cdot cos \, \beta$ [1]

Restando: 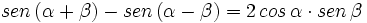$sen \, (\alpha + \beta) -sen \, (\alpha - \beta)= 2 \, cos \, \alpha \cdot sen \, \beta$ [2]

Hacemos los siguientes cambios de variable: $\begin{cases} \alpha + \beta = A \\ \alpha - \beta = B \end{cases}$

Resolviendo este sistema:

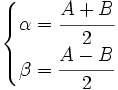
$\begin{cases} \alpha = \cfrac{A+B}{2} \\ \beta = \cfrac{A-B}{2} \end{cases}$

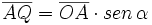
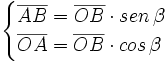
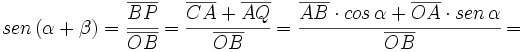
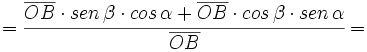
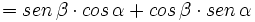
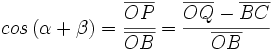
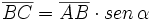
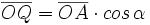
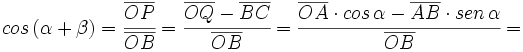
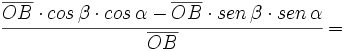
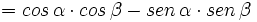
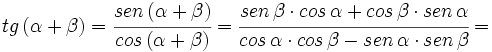
que sustituidas en [1] y [2] nos da V.1 y V.2.

Ejemplo: Transformaciones de sumas en productos

Transforma en producto y calcula: $sen \, 75^\circ -sen \, 15^\circ$ .

Solución:

$sen \, 75^\circ -sen \, 15^\circ= 2 \, cos \, \cfrac{75^\circ+15^\circ}{2} \cdot sen \, \cfrac{75^\circ-15^\circ}{2}= 2 \, cos \, 45^\circ \cdot sen \, 30^\circ= 2 \, \cfrac{\sqrt{2}}{2}\cdot \cfrac{1}{2}=\cfrac{\sqrt{2}}{2}$

Obtenido de "http://maralboran.org/wikipedia/index.php/F%C3%B3rmulas_trigonom%C3%A9tricas_%281%C2%BABach%29"

Categorías: Matemáticas | Geometría | Funciones

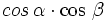 ::::<math>=\cfrac{\cfrac{sen \, \beta \cdot cos \, \alpha}{cos \, \alpha \cdot \cos \, \beta} + \cfrac{cos \, \beta \cdot sen \,  \alpha}{cos \, \alpha \cdot \cos \, \beta}}{\cfrac{cos \, \alpha \cdot cos \, \beta}{cos \, \alpha \cdot \cos \, \beta} - \cfrac{sen \, \alpha \cdot sen \,  \beta}{cos \, \alpha \cdot \cos \, \beta}}=\cfrac{tg \, \beta + tg \, \alpha}{1-tg \, \alpha \cdot tg \, \beta}</math>
+}}
+{{p}}
+{{Video_enlace
+|titulo1=Razones trigonométricas de la suma de dos ángulos
+|duracion=12´41
+|url1=http://www.youtube.com/watch?v=b1C_O92pECI
+|sinopsis=Videotutorial.
 }}
 {{p}}
 }}
 {{p}}
-{{p}}
+{{ejercicio
+|titulo=Ejercicios
+|cuerpo=
 {{Video_enlace
-|titulo1=Razones trigonométricas de la suma de dos ángulos
+|titulo1= 3 ejercicios
-|duracion=12´41
+|duracion=5´23"
-|url1=http://www.youtube.com/watch?v=b1C_O92pECI
+|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/1101-tres-ejercicios-seno-coseno-y-tangente-de-la-suma-de-tres-angulos#.VCrhiha7ZV8
-|sinopsis=Videotutorial.
+|sinopsis=Seno, coseno y tangente de la suma de tres ángulos.
+}}
 }}
 {{p}}
 ==Razones trigonométricas de la diferencia de dos ángulos==
 {{Teorema|titulo=Razones trigonométricas de la diferencia de dos ángulos

Fórmulas trigonométricas (1ºBach)

De Wikipedia

Revisión de 17:03 30 sep 2014

Tabla de contenidos

Razones trigonométricas de la suma de dos ángulos

Razones trigonométricas de la diferencia de dos ángulos

Razones trigonométricas del ángulo doble

Razones trigonométricas del ángulo mitad

Transformaciones de sumas y diferencias de senos y cosenos en productos

Vistas

Herramientas personales

Menú

Buscar

Herramientas