Plantilla:Números compuestos y números primos
De Wikipedia
| Revisión de 08:53 20 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:07 7 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C. | La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C. | ||
| <br> | <br> | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Criba de Eratóstenes''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Practica el algoritmo de la criba de Eratóstenes. | ||
| - | |actividad= | ||
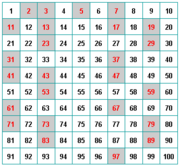
| - | La Criba de Eratóstenes es un procedimiento para obtener los primeros números primos. | ||
| - | * Se comienza con un panel en el que están colocados los números naturales a partir del número 2. Normalmente se hace con los cien primeros números naturales, aquí emplearemos solamente hasta el número 46. | ||
| - | * Comenzamos por el número 2, lo dejamos, pero a partir de él contamos de 2 en 2 y eliminamos los números que sean múltiplos de 2. | ||
| - | * El primer número de los que quedan es el 3, lo dejamos y desde el número 3 eliminamos los números que sean múltiplos de 3. | ||
| - | * El siguiente número de los que quedan es el 5, lo dejamos y desde el número 5 eliminamos los números que sean múltiplos de 5. | ||
| - | * Así vamos avanzando, cuando llegamos a un número que no ha sido eliminado lo dejamos, pero a partir de él eliminamos los números que sean múltiplos de él. Así hasta el final. | ||
| - | * Finalmente habrán quedado solamente números primos. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/criba_1.html | ||
| - | width=650 | ||
| - | height=470 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/criba_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| ===Cómo averiguar si un número es primo=== | ===Cómo averiguar si un número es primo=== | ||
| Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo). | Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo). | ||
| Línea 66: | Línea 44: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Números primos y compuestos''|cuerpo= | + | {{wolfram |
| - | {{ai_cuerpo | + | |titulo=Actividad: ''Valor numérico de una expresión algebraica'' |
| - | |enunciado=1. Descubre si un número es primo o compuesto. | + | |cuerpo= |
| - | |actividad= | + | {{ejercicio_cuerpo |
| - | Marca el número que quieras en la ventana del control inferior y pulsa intro, después puedes ir variando el valor del número de uno en uno utilizando los triángulos arriba y abajo. | + | |enunciado= |
| - | El ordenador te indicará si ese número es primo o compuesto. En caso de ser compuesto te indicará además por qué número se le puede dividir después del 1. | + | |
| - | El número más grande que puedes marcar es el 10.000.000.000 | + | |
| - | <center><iframe> | + | :a) ¿Es 63 un número primo? |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/primos_1.html | + | :b) ¿Es 181 un número primo? |
| - | width=400 | + | {{p}} |
| - | height=420 | + | |sol= |
| - | name=myframe | + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/primos_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | '''Investiga y contesta en tu cuaderno:''' | + | |
| - | a) Desde el número 2, utilizando el triángulo arriba, aumenta de uno en uno y cuenta los números primos que hay en la primera centena desde el 2 hasta el 101. | + | :a) {{consulta|texto=is 63 a prime number?}} |
| + | :a) {{consulta|texto=is 181 a prime number?}} | ||
| - | b) Marca después un número de 9 cifras, comienza con uno que termine en 00, aumenta de uno en uno y haz el recuento de los números primos que encuentres en esa centena. | + | {{widget generico}} |
| - | + | ||
| - | c) ¿Qué deduce? | + | |
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
Revisión de 19:07 7 oct 2014
Un número natural es compuesto si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número primo. Propiedad: Un número primo sólo tiene por divisores a la unidad y a él mismo. |
Video: Números naturales. Números primos (17´)
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos
números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo para hallar números primos que desarrolló el célebre matemático griego Eratóstenes en el siglo III a.C.
Cómo averiguar si un número es primo
Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).
Ejemplo: Averiguar si un número es primo
- Averigua si el número 167 es primo.
Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:
- Dividimos 167 entre 2: cociente=83 y resto=1. No es divisible por 2.
- Dividimos 167 entre 3 porque 83>3: cociente=55 y resto=2. No es divisible por 3.
- Dividimos 167 entre 5 porque 55>5: cociente=33 y resto=2. No es divisible por 5.
- Dividimos 167 entre 7 porque 33>7: cociente=23 y resto=6. No es divisible por 7.
- Dividimos 167 entre 11 porque 23>11: cociente=15 y resto=2. No es divisible por 11.
- Dividimos 167 entre 13 porque 15>13: cociente=12 y resto=11. No es divisible por 13.
- Paramos y no dividimos 167 entre 17 porque 12<17.
|
Actividad: Valor numérico de una expresión algebraica
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
 .
.